作者 | 张文,浙江大学博士,研究兴趣为知识图谱表示与推理
陈名杨,浙江大学在读博士生,研究兴趣为知识图谱表示与推理
本文将介绍近两年4篇关于知识图谱中的复杂查询问答(Complex Query Answering, CQA)的研究工作。复杂查询问答的目标是回答针对知识图谱的逻辑查询,例如:
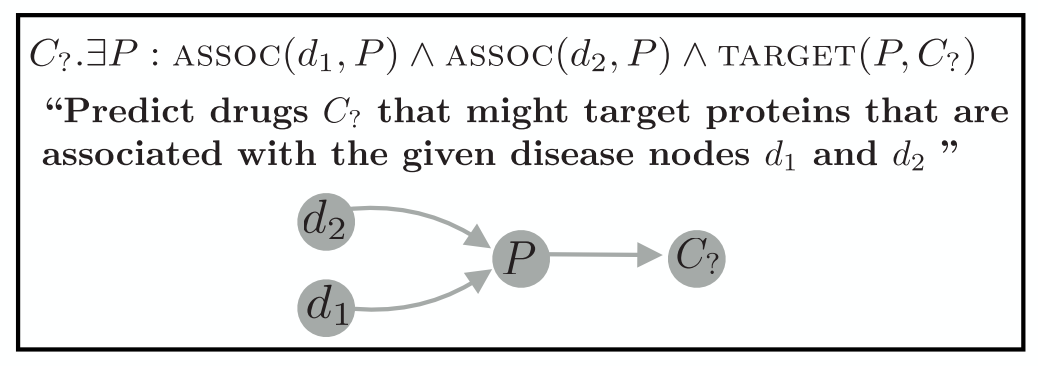
查询语句由逻辑符号组成,包括存在量词( )、逻辑合取( )、逻辑析取( )、逻辑否定( )等。
复杂查询问答的两个重要挑战是:
(1)知识图谱往往是不全的,因此查询语句中的原子可能涉及不存在在知识图谱中的但是正确的三元组,因此依靠纯符号匹配的方法无法保证查询结果的完整性;
(2)知识图谱中包含实体之间错综复杂的关系,因此知识图谱中可能有很多满足查询的子图,当知识图谱规模较大时,查询效率较低。
因此本文介绍的研究寻求在通过计算来解决复杂查询问答任务,将查询问答从符号匹配的范式迁移到基于计算的范式上。
Embedding Logical Queries on Knowledge Graphs
发表会议:NeurlPS 2018
这篇文章是首先提出复杂查询问答的研究工作,其重点解决了由存在量词( )和逻辑合取( )组成的合取查询问答,合取查询可以定义为如下:
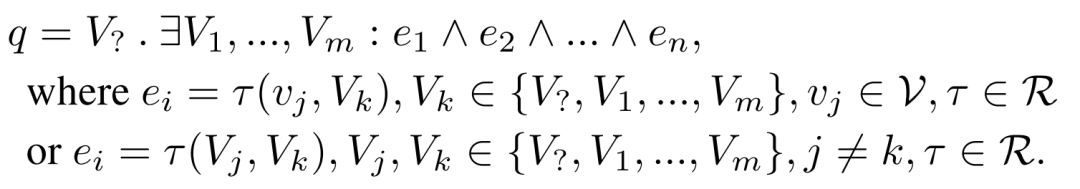
即合取查询语句是由一系列逻辑合取( )连接的原子( )组成,每个原子由一个锚点实体( )和实体变量( )组成,或是由两个实体变量组成。其中锚点实体指的是在查询语句中给定的实体。查询语句举例如下:
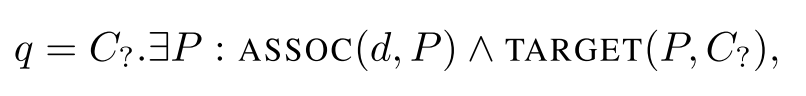
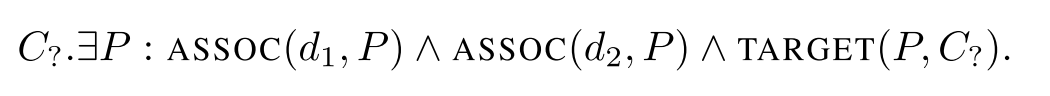
这篇文章提出的基本思路是:将查询语句表示为向量,通过计算查询语句向量和实体向量之间的相似度完成回答。在进行查询计算前,首先会将查询语句表示为一个查询图(Graph Query),然后根据查询图的结构进行查询计算,因此这篇文章将提出的方法命名为GQE(Graph Query Embedding), 给定一个查询,其计算流程下图所示:

为了将查询语句表示为向量,这篇文章提出了两种算子:
一个是映射算子,用于将一个头实体的向量表示映射到通过某个关系连接后的尾实体表示,文中采用了线性映射假设:

一个是合取算子,用于计算两个表示实体集合的向量的交集,可以得到查询语句中两个逻辑合取连接的原子的结果,文中采用如下计算方式:
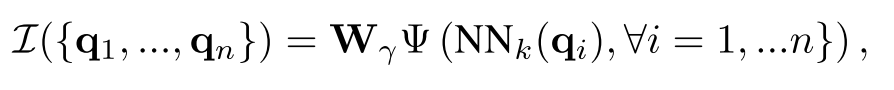
其中 是需要进行合取计算的原子表示, 是一个顺序无关的计算函数, 是一个线性变换矩阵。
在训练时,采用融合负采样的基于间隔的损失函数,并提出了两种不同难度的负样本采样方法。作者在两个构造的CQA数据集验证了GQE的有效性,部分实验结果如下:

Query2Box: Reasoning Over Knowledge Graphs In Vector Space Using Box Embeddings
发表会议:ICLR 2019
作者认为先前的方法存在两个问题,第一是先前的方法将查询嵌入到向量空间中一个单一的点上,但是在实际的逻辑查询中,往往需要建模一个实体的集合,然而这种集合用点来表示会造成困扰;第二点是之前的工作只考虑了逻辑合取,仅仅是一阶逻辑中的一小部分,没有考虑析取。
这篇文章提出Query2Box的方法Q2B,将查询过程中的实体建模成Box Embeddings,其中一个box是由中心(Center)和偏移(Offset)表示的,一个在 中的box表示为 ,如下:

将查询中的操作建模成在box之间的操作如下:
projection operation:把每个关系表示成
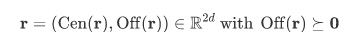
对于给定的box embedding 和关系 ,映射操作通过 完成,也就是分别相加中心和偏移;
interp operation:interp的操作是在一个box embedding的集合上进行计算,具体操作如下
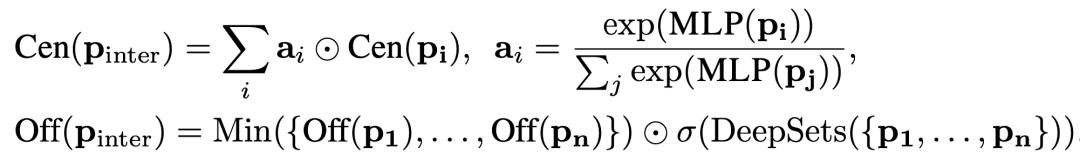
除此之外,box之间的距离计算方式是由两部分相加得到,外部距离和内部距离,
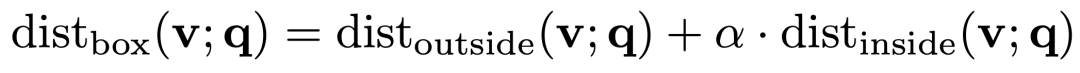
其中两部分的具体计算方法如下:

上面所述的projection,interp和计算距离的图示如下图
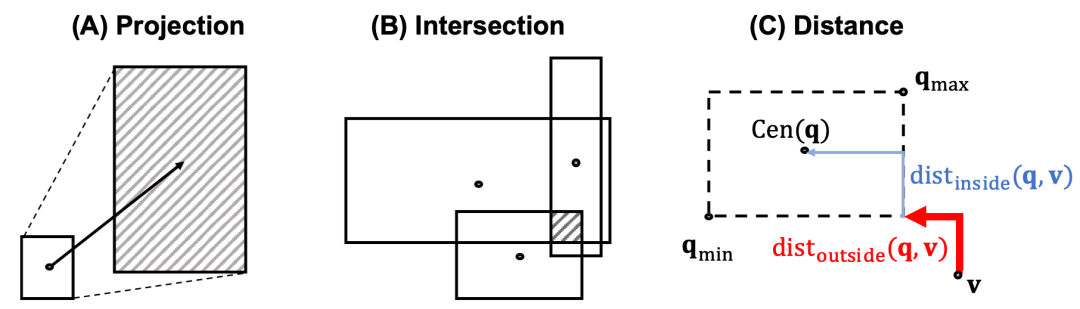
模型的训练采用的依然是常见的负采样的loss,如下
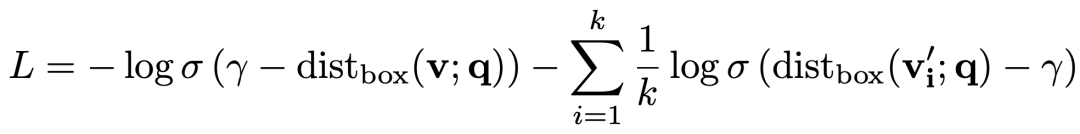
本篇文章对于析取的处理方式是将包含析取的逻辑查询转换成析取范式(DNF),也就是多个合取式的析取,这样只需要在最后一步处理析取的操作,计算一个候选实体和一个包含析取范式的查询 之间的距离如下,
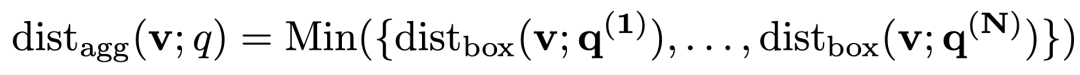
作者在如下前五种的查询形式下进行训练,并在所有九种形式上测试,

最终的实验结果如下:
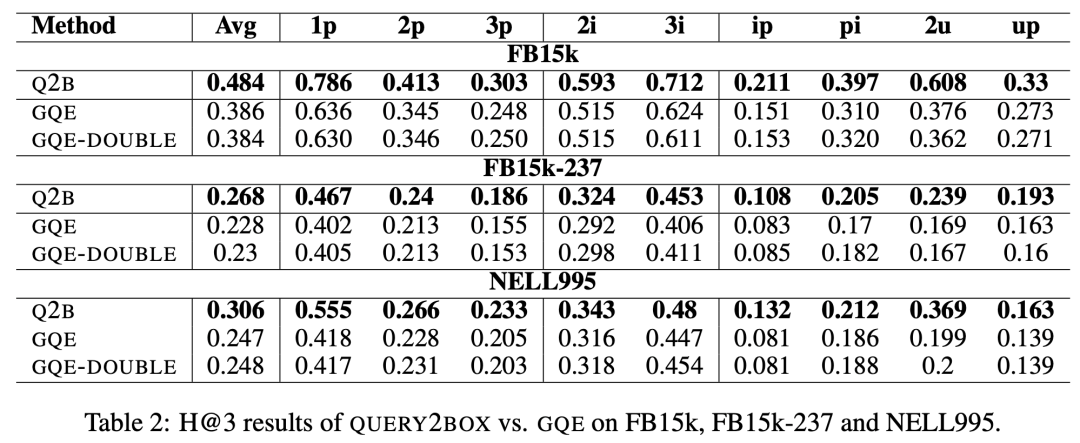
Beta Embeddings for Multi-Hop Logical Reasoning in Knowledge Graphs
发表会议:NeurlPS 2020
这篇文章在之前介绍的两篇文章的基础上将逻辑析取( )、逻辑否定( )考虑进了查询语句中。GQE和Q2B方法均不能直接应用于逻辑否定( ),因为他们将实体表示为一个向量或Box,而向量或Box表示进行否定后均不是闭合空间,会导致整个CQA问题的计算发生在不可控的非闭合空间中。
为了解决这个问题,这篇文章提出了将实体表示为Beta分布,因此将方法命名为BetaE。Beta分布有两个重要的参数 , 其概率密度函数如下:
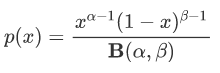
每个实体/子查询的表示用以下符号表示:
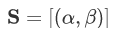
BetaE中包含三种算子用于查询图上的计算,包括前文提到的映射算子和合取算子,以及一个新提出的否定算子:
(1)映射算子:通过与关系相关的多个全连接层神经网络将输入的实体Beta分布映射为尾实体的Beta分布。
(2)合取算子:通过attention机制,将多个输入的Beta分布融合为一个新的Beta分布:
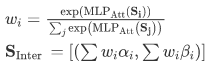
一个合取算子的例子如下:
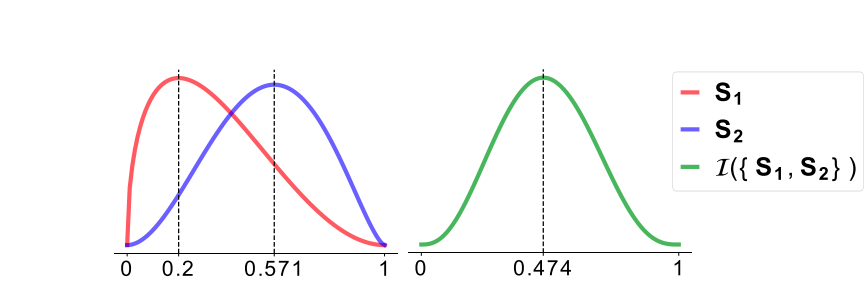
(3) 否定算子:否定算子的目的是将原来概率较高的区域变成较低的,同时原来概率较低的区域变成较高的,因此设计为
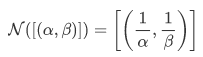
原分布和取否定之后的分布可视化如下:

在训练过程中,通过计算查询语句的Beta分布和目标实体的Beta分布之间的KL散度估计两者的相似度,并采用了如下基于负采样的损失函数:
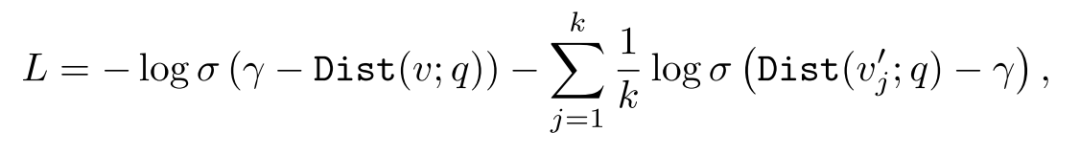
对于逻辑析取( )的处理,这篇文章提出了两种方法:一种是通过De Morgan’s laws (DM) 将包含逻辑析取( )的查询语句转换为只包含逻辑合取( )和逻辑否定( )的查询语句,一种是将其转换为析取范式(Disjunction Normal Form, DNF)。
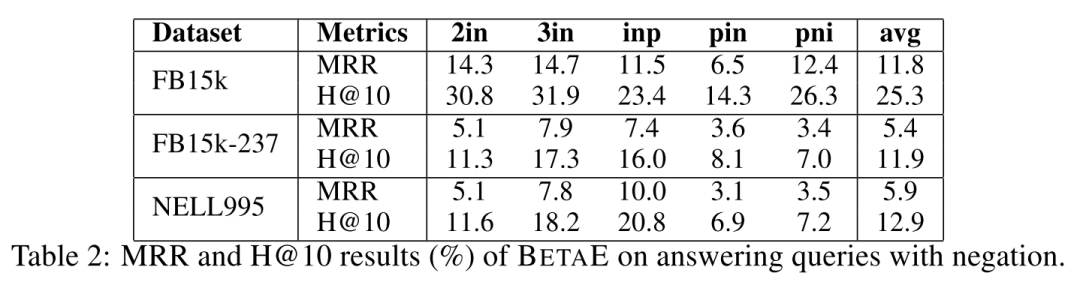
实验过程中,作者将BetaE在如下形式的查询语句上进行了验证:
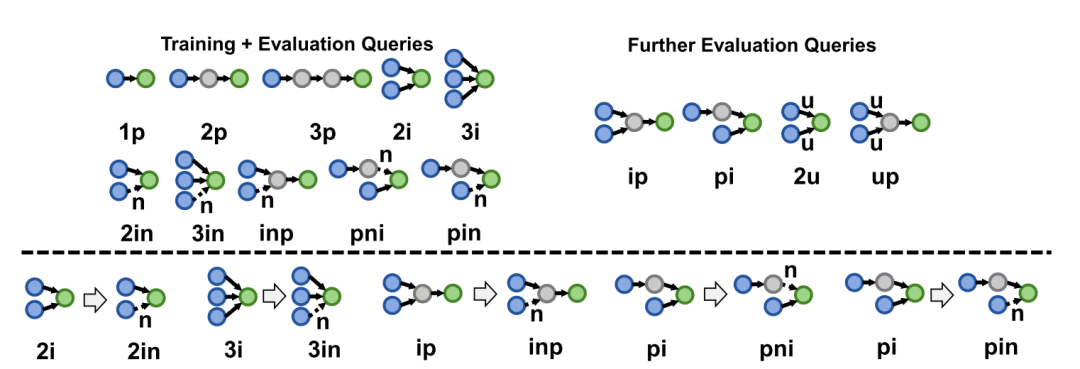
实验结果如下:
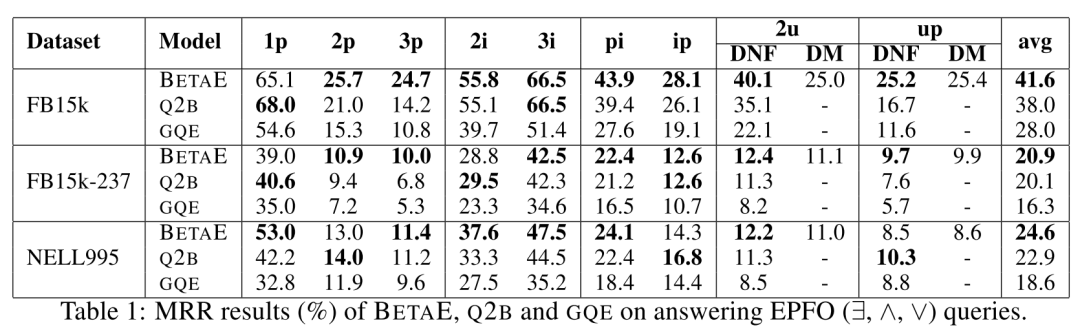
Complex Query Answering With Neural Link Prediction
发表会议:ICLR 2021
先前的文章都把重点放在如何对带有逻辑的查询进行嵌入表示,并且训练的过程中需要上百万的不同种类的逻辑查询的训练数据。本篇文章试图提出利用一种更高效的神经链接预测器(Neural Link Predictor)仅仅在单跳(1-hop)的逻辑查询e问答上进行训练学习后,进而泛化到更多的种类的复杂查询问答。
本篇文章针对的问题和前面的文章类似,针对带有存在量词( )、逻辑合取( )、逻辑析取( )的复杂逻辑查询,但并未考虑逻辑否定( )。
首先介绍方法中的两个重要概念:
Neural Link Prediction:指的是可以将一个三元组(这里也叫做原子atom)的组成部分映射到向量空间,然后对该三元组计算分数。本质上就是一个score function对三元组计算真值。这里使用的是ComplEx的方法。
T-Norms:t-norm如 是逻辑合取的一种拓展,允许将离散的逻辑操作拓展到数值上的计算,有多种不同的t-nrom,例如product t-norm 。t-conorms是t-norms的对偶形式用于逻辑析取。
接下来对于一个复杂逻辑查询表达为析取范式如下:
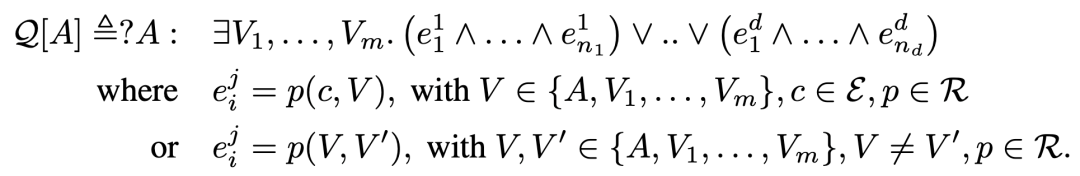
我们将其利用上面提到的neural link predictor和t-norms将其转换为一个可以优化的问题为:
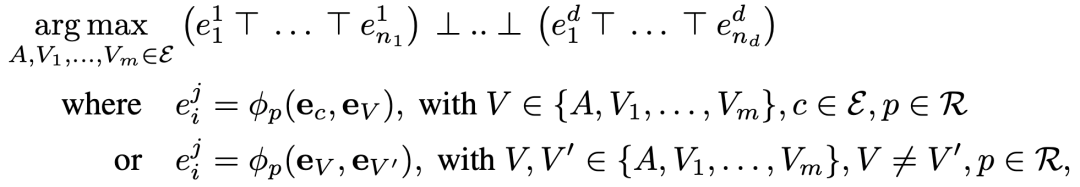
其中 和 表示t-nrom和t-conorm, 代表通过用neural link predictor计算出来的对原子
计算出来的分数。
对于上面这个优化问题,文章提出两种优化方法:
Continuous Optimization:简单来说就是找到能够让上面这个优化问题最优的 的表示,然后然后把候选的实体表示替代 的位置,找出能让查询最终分数最大化的实体最为最终的查询答案。
Combination Optimization:利用贪婪搜索的方法对每个位置进行实体替换,从而找到能让优化问题最优的答案,类似于beam search的操作。
在实验的过程中,因为该模型只需要训练一个neural link predictor,所以只需要在原子上,也就是1-hop的逻辑查询上进行训练,进而拓展到以下形式的查询

最终的实验结果如下
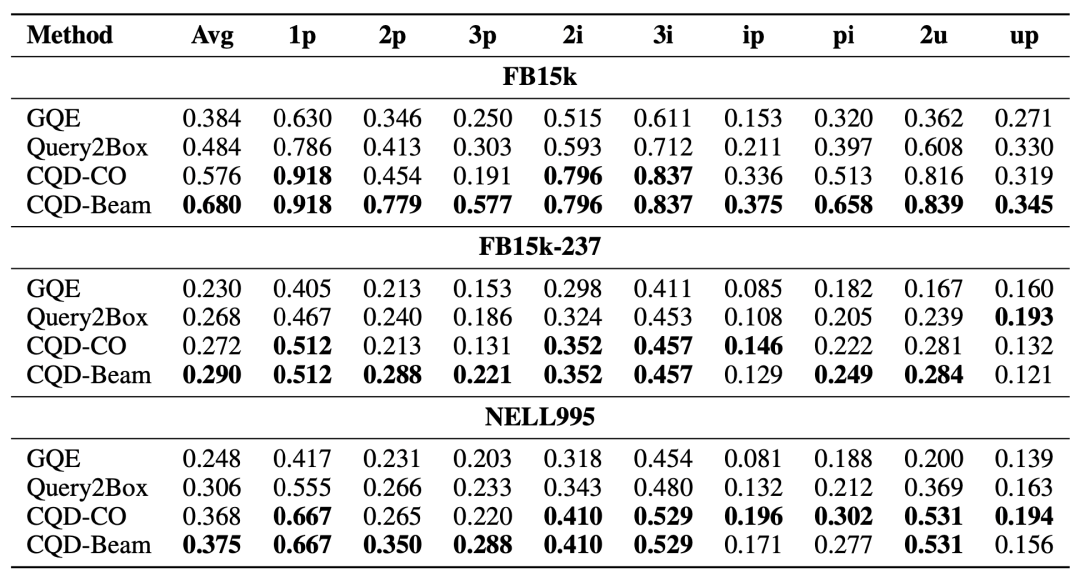
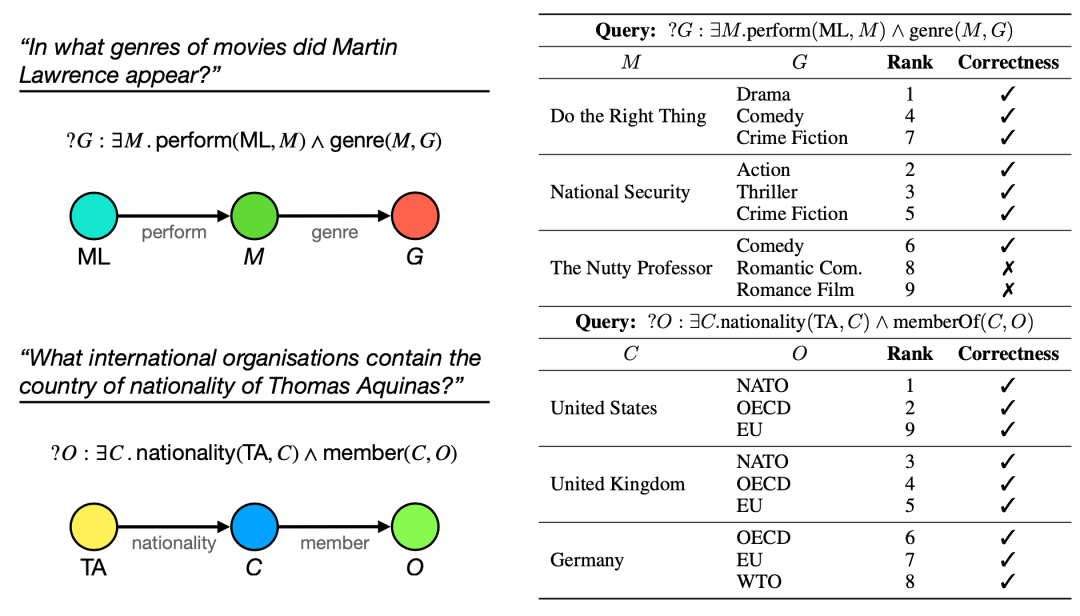
并且利用Combination Optimization的方法进行查询的话,还可以得到查询的中间答案,对最终的结果进行解释,示例如下


浙江大学知识引擎实验室
OpenKG
开放知识图谱(简称 OpenKG)旨在促进中文知识图谱数据的开放与互联,促进知识图谱和语义技术的普及和广泛应用。

点击阅读原文,进入 OpenKG 网站。