web架构师编辑器内容-使用html2canvas获取截图，并处理一些问题

html2canvas-api
为了使用html2canvas完成截图的功能，我们首先先使用一个按钮来测试一下html2canvas的截图功能。

首先在页面上创建一个img标签

<img id="test-image" :style="{ width: '300px'}"/>

创建一个button按钮，添加点击事件publish

<button @click="publish">发布</button>
const publish = () => {const el = document.getElementById('canvas-area') as HTMLElement;// 引入html2canvas, 调用html2canvas，返回一个promise对象 // 第二个参数是 html2canvas的options，先添加一下最终截图的宽度html2canvas(el, { width: 375 }).then((canvas) => {// 返回一个canvas Element,将该element显示到图片上面const image = document.getElementById('test-image') as HTMLImageElement;// toDataURL可以将canvas转换成一系列base64编码的图片资源内容image.src = canvas.toDataURL();});
};

第一个问题是没有背景图片了

在这里插入图片描述
这是因为我们页面上面的元素都是使用的是阿里云的oss，所以图片的地址会存在跨域的情况，htmlCanvas对于任何跨域的资源都不会做处理，所以就不会显示截图出现的背景图片。
解决方法：

// 在options里面，增加 useCORS来处理跨域请求。
html2canvas(el, { width: 375, useCORS: true })

在请求头里面：
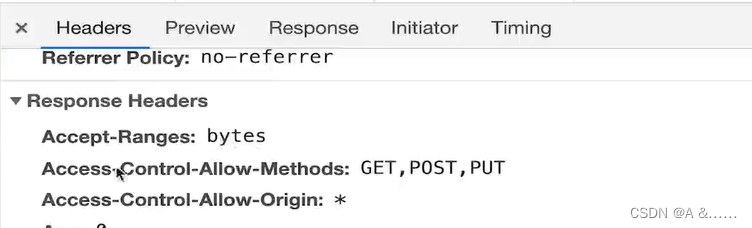
在这里插入图片描述
当然这个配置生效的前提是要在我们阿里云oss中进行跨域请求的一些配置，否则还是不会生效的。
对象存储 --> 权限管理 --> 跨域访问

第二个问题是html2canvas获取到的截图在某些机型上面得到的宽度是750px，但是我们设置的宽度是375。

主要原因是window.devicePixelRatio的值不同
window.devicePixelRatio
https://developer.mozilla.org/zh-CN/docs/Web/API/Window/devicePixelRatio
返回当前显示设备的物理像素分辨率与CSS像素分辨率之比。简单来说，它告诉浏览器应使用多少屏幕实际像素来绘制单个CSS像素。

在一个标准的显示密度下，所以在标准屏幕下，devicePixelRatio 应该为 1

特例
视网膜（Retina）显示屏，它会使用更多的屏幕像素绘制相同的对象，从而获得更清晰的图像。devicePixelRatio 为 2 。

所以虽然我们中间的元素 css 尺寸是 375px，但是因为 Apple 是视网膜屏幕，所以使用了两倍于 css 尺寸的设备像素来渲染它，这就是最后图片尺寸为 750 px 的原因。

html2canvas 的处理

https://html2canvas.hertzen.com/configuration/ 中的 scale 属性

html2canvas(el, { width: 375, useCORS: true, scale: 1 })

第三个问题是有的区域出现了灰色黑色的区域

在这里插入图片描述
出现这个原因是因为我们在进行渲染中间画布区域的时候会带上一个boxShadow属性：

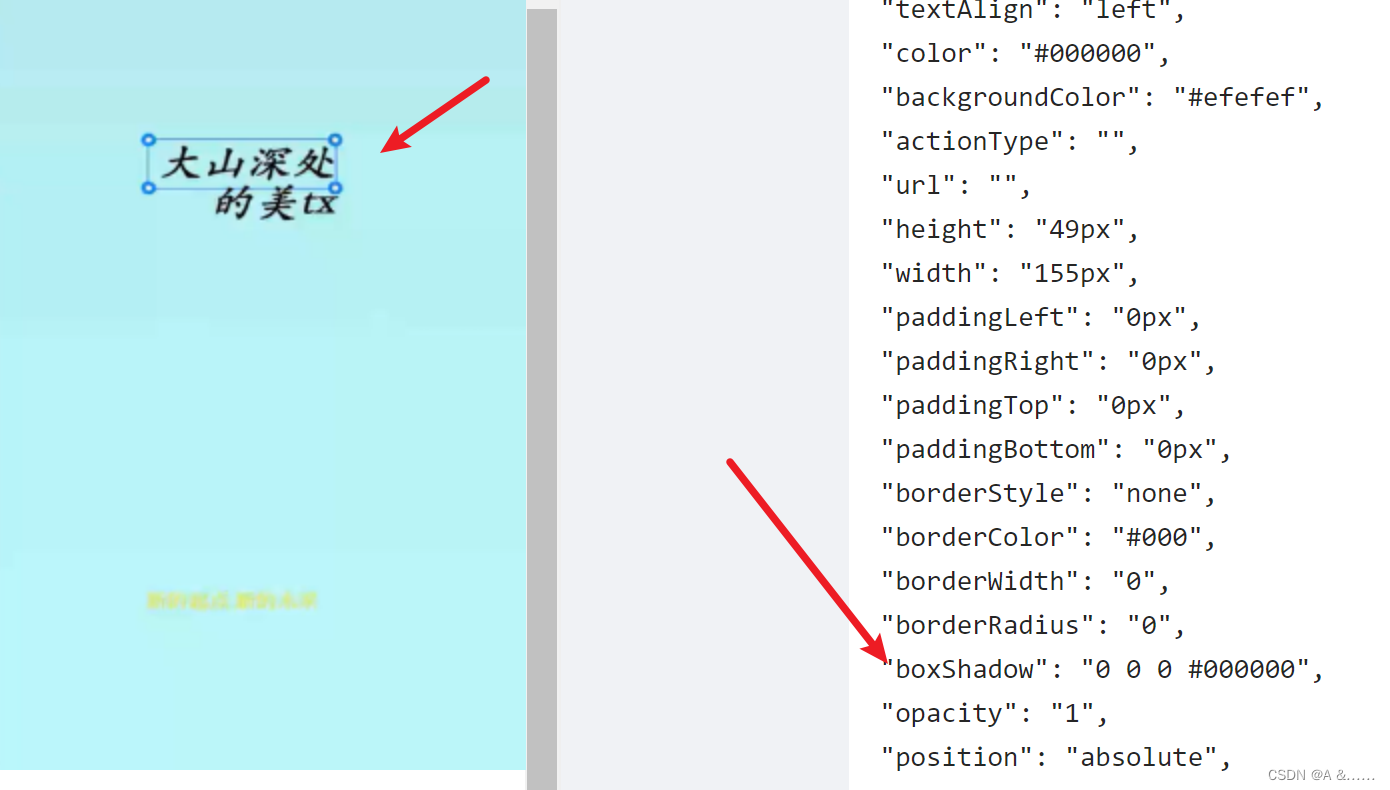
html2canvas是不支持boxShadow渲染的，一旦有这个属性就会出现这个问题。解决方法就是我们需要手动动态增加一些类名，然后去掉这个属性

    const canvasFix = ref(false)const publish = async () => {// remove select element,主要是将蓝色选中状态去掉store.commit('setActive', '');const el = document.getElementById('canvas-area') as HTMLElement;canvasFix.value = true;// 需要等dom更新后进行截图，效果才能上去。await nextTick();html2canvas(el, { width: 375, useCORS: true, scale: 1 }).then((canvas) => {const image = document.getElementById('test-image') as HTMLImageElement;image.src = canvas.toDataURL();canvasFix.value = false;});};// 通过canvasFix来动态增加类型，将box-shadow干掉.preview-list.canvas-fix .edit-wrapper > * {box-shadow: none !import;}