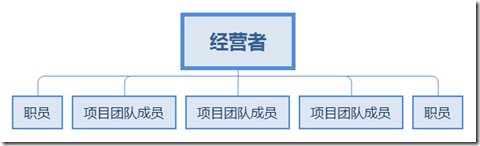
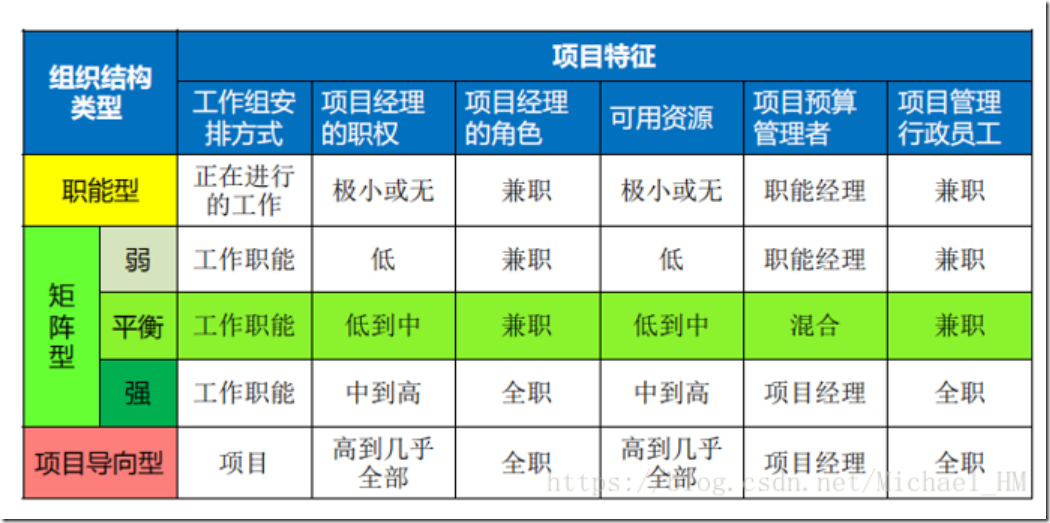
1.简单型
描述:人员并肩工作,所有者/经营者直接做出主要决定并监督执行。
PM角色:兼职(协调员)
PM权限:极少(无)
项目管理人员:极少(无)
资源可用性:极少(无)
项目预算管理人:负责人
2.职能型组织
描述:按分工原则,按职能划分部门
PM角色:兼职(协调员)
PM权限:极少(无)
项目管理人员:兼职
资源可用性:极少(无)
项目预算管理人:职能经理
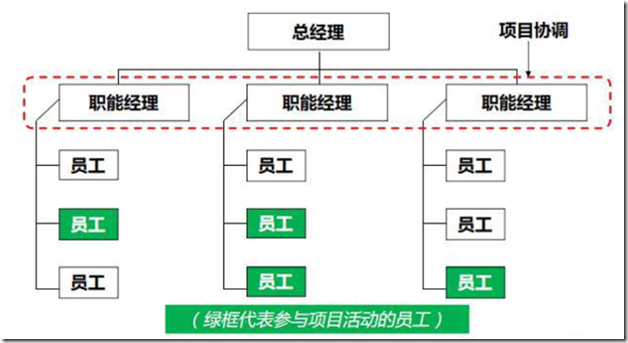
优点:清楚的上下级关系,按职能专业组织的团队易于提高专业技术
缺点:职能部门利益优于项目,项目间的跨部门沟通困难,妨碍客户参与项目。项目经理对项目没有足够的控制授权,分层级的决策影响对问题的反应速度。
3.多部门
描述:公司总部将各部门日常运营和部门决策授权给项目经理
PM角色:兼职(协调员)
PM权限:极少(无)
项目管理人员:兼职
资源可用性:极少(无)
项目预算管理人:职能经理
4.弱矩阵型组织
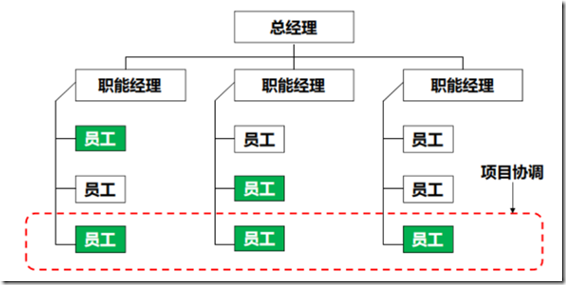
在弱矩阵中,PM是项目联络员或者协调员
项目联络员和协调员有区别:
项目联络员:联络沟通作用,没有权力,需要职能经理做决定。
项目协调员:有一定的决策权、可以向高层经理汇报,打小报告。
比起职能型组织,弱矩阵的优点是加强了部门间的沟通。
PM 兼职 权利小于职能经理
5.平衡矩阵组织
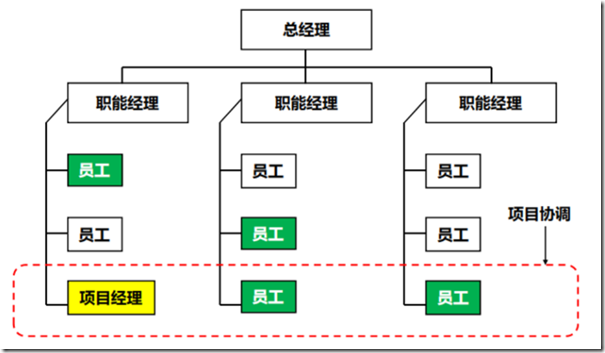
该组织为缺省组织,如果题干中没具体说明是什么组织,则默认组织为平衡矩阵
优点:资源使用率高
缺点:员工要听2个领导的
PM 全职 权利等于职能经理
6.强矩阵组织
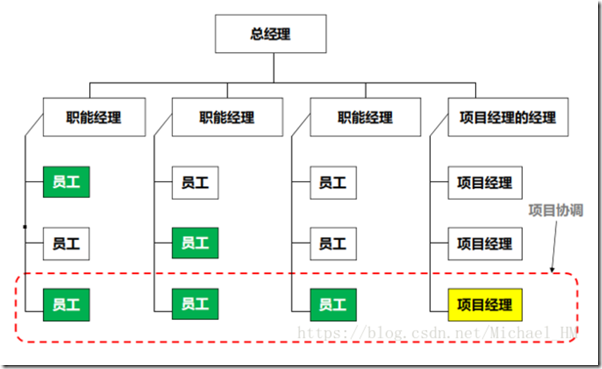
优点:兼顾项目与职能工作,资源使用率更高,比职能型组织部门间沟通更好
缺点:一个员工有 2 个汇报对象(pm 和职能经理),沟通复杂。
PM 全职 权利大于职能经理
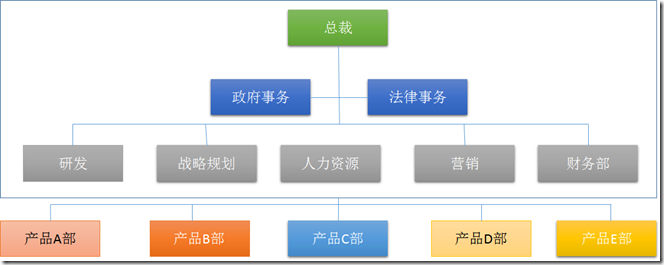
7.项目型组织
描述:以项目划分组织单元,项目完成,组织单元终结。
PM角色:全职
PM权限:高到几乎全部
项目管理人员:全职
资源可用性:高到几乎全部
项目预算管理人:项目经理
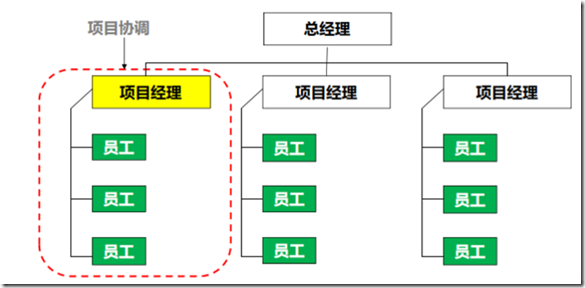
优点:pm 权力充分,团队职责清晰,沟通容易,对项目的反应速度非常快。
缺点:员工缺乏归属感、缺乏事业的连续性和保障,资源配置重复使用效率低。
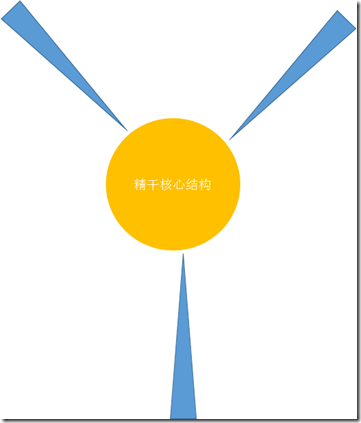
8.虚拟型
描述:只有精干核心结构,以契约关系的建立和维持为基础组织人员,实现目标的临时组织。
PM角色:全职/兼职
PM权限:低到中
项目管理人员:全职/兼职
资源可用性:低到中
项目预算管理人:混合
9.混合型
描述:二种以上组织结构混合
PM角色:混合
PM权限:混合
项目管理人员:混合
资源可用性:混合
项目预算管理人:混合
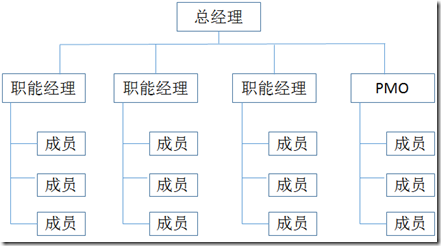
10.PMO型
描述:项目、项目集、项目组合混合
PM角色:全职
PM权限:高到全部
项目管理人员:全职
资源可用性:高到几乎全部
项目预算管理人:项目经理
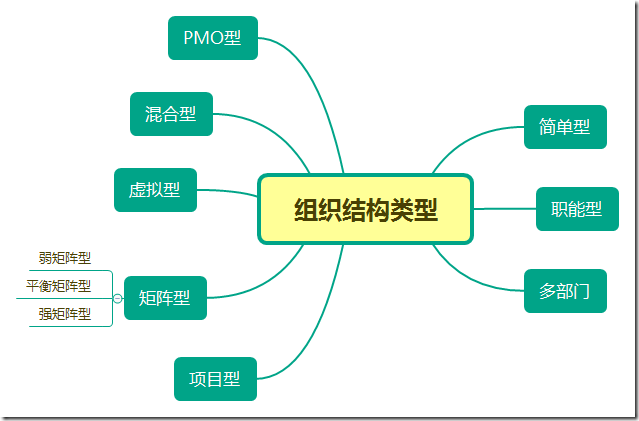
三大类组织结构总结如下:
1)职能型:适合专业技能单一、在部门内开展简单项目活动;
2)矩阵型:适合跨部门、跨专业的项目,提高资源的使用效率;
3)项目型:适合项目难度高、风险大,需要团队全身心投入,pm 最大限度的掌握项目资源。
![[Leetcode][第96题][JAVA][不同的二叉搜索树][动态规划][数学]](http://pic.xiahunao.cn/[Leetcode][第96题][JAVA][不同的二叉搜索树][动态规划][数学])

![[剑指offer]面试题第[61]题[JAVA][扑克牌中的点数][HashSet][数组]](http://pic.xiahunao.cn/[剑指offer]面试题第[61]题[JAVA][扑克牌中的点数][HashSet][数组])
![[剑指offer]面试题第[65]题[JAVA][不用加减乘除做加法][位运算]](http://pic.xiahunao.cn/[剑指offer]面试题第[65]题[JAVA][不用加减乘除做加法][位运算])
H.封印之门 最短路)
![[密码学基础][每个信息安全博士生应该知道的52件事][Bristol Cryptography][第4篇] P类复杂问题](http://pic.xiahunao.cn/[密码学基础][每个信息安全博士生应该知道的52件事][Bristol Cryptography][第4篇] P类复杂问题)


![[密码学基础][每个信息安全博士生应该知道的52件事][Bristol Cryptography][第5篇]复杂性类NP是什么意思?](http://pic.xiahunao.cn/[密码学基础][每个信息安全博士生应该知道的52件事][Bristol Cryptography][第5篇]复杂性类NP是什么意思?)


![[密码学基础][每个信息安全博士生应该知道的52件事][Bristol Cryptography][第6篇]我们怎么把NP问题解释成一组可以在多项式内证明的命题](http://pic.xiahunao.cn/[密码学基础][每个信息安全博士生应该知道的52件事][Bristol Cryptography][第6篇]我们怎么把NP问题解释成一组可以在多项式内证明的命题)


![[Leetcode][第785题][JAVA][判断二分图][BFS][DFS]](http://pic.xiahunao.cn/[Leetcode][第785题][JAVA][判断二分图][BFS][DFS])
![[剑指offer]面试题第[68-2]题[Leetcode][第236题][JAVA][二叉搜索树的最近公共祖先][递归]](http://pic.xiahunao.cn/[剑指offer]面试题第[68-2]题[Leetcode][第236题][JAVA][二叉搜索树的最近公共祖先][递归])

![[密码学基础][每个信息安全博士生应该知道的52件事][Bristol Cryptography][第7篇]随机性如何辅助计算和什么是BPP类问题](http://pic.xiahunao.cn/[密码学基础][每个信息安全博士生应该知道的52件事][Bristol Cryptography][第7篇]随机性如何辅助计算和什么是BPP类问题)

