【问题描述】[中等]

【解答思路】

1. 动态规划

第 1 步：设计状态

第 2 步：状态转移方程

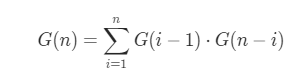
第 3 步：考虑初始化

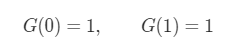
第 4 步：考虑输出

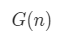
时间复杂度：O(N^2) 空间复杂度：O(N)

public int numTrees(int n) {int[] G = new int[n + 1];G[0] = 1;G[1] = 1;for (int i = 2; i <= n; ++i) {for (int j = 1; j <= i; ++j) {G[i] += G[j - 1] * G[i - j];}}return G[n];}

2. 数学公式

时间复杂度：O(N) 空间复杂度：O(1)

public int numTrees(int n) {// 提示：我们在这里需要用 long 类型防止计算过程中的溢出long C = 1;for (int i = 0; i < n; ++i) {C = C * 2 * (2 * i + 1) / (i + 2);}return (int) C;}

【总结】

1. 动态规划流程

第 1 步：设计状态
第 2 步：状态转移方程
第 3 步：考虑初始化
第 4 步：考虑输出
第 5 步：考虑是否可以状态压缩

2.卡塔兰数 C_n

​

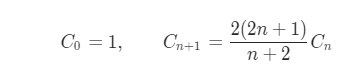
3.二叉树 找规律 动态规划 画图递归

转载链接：https://leetcode-cn.com/problems/unique-binary-search-trees/solution/bu-tong-de-er-cha-sou-suo-shu-by-leetcode-solution/