[Leetcode][第114题][JAVA][二叉树展开为链表][递归][迭代]

【问题描述】[中等]

在这里插入图片描述

【解答思路】

1. 前序遍历

将二叉树展开为单链表之后，单链表中的节点顺序即为二叉树的前序遍历访问各节点的顺序。因此，可以对二叉树进行前序遍历，获得各节点被访问到的顺序。
由于将二叉树展开为链表之后会破坏二叉树的结构，因此在前序遍历结束之后更新每个节点的左右子节点的信息，将二叉树展开为单链表。

时间复杂度：O(N) 空间复杂度：O(N)
在这里插入图片描述

递归（自上而下）

class Solution {public void flatten(TreeNode root) {List<TreeNode> list = new ArrayList<TreeNode>();preorderTraversal(root, list);int size = list.size();for (int i = 1; i < size; i++) {TreeNode prev = list.get(i - 1), curr = list.get(i);prev.left = null;prev.right = curr;}}public void preorderTraversal(TreeNode root, List<TreeNode> list) {if (root != null) {list.add(root);preorderTraversal(root.left, list);preorderTraversal(root.right, list);}}
}

迭代
时间复杂度：O(N) 空间复杂度：O(N)

class Solution {public void flatten(TreeNode root) {List<TreeNode> list = new ArrayList<TreeNode>();Deque<TreeNode> stack = new LinkedList<TreeNode>();TreeNode node = root;while (node != null || !stack.isEmpty()) {while (node != null) {list.add(node);stack.push(node);node = node.left;}node = stack.pop();node = node.right;}int size = list.size();for (int i = 1; i < size; i++) {TreeNode prev = list.get(i - 1), curr = list.get(i);prev.left = null;prev.right = curr;}}
}

2. 前序遍历和展开同时进行

在这里插入图片描述

时间复杂度：O(N) 空间复杂度：O(N）
在这里插入图片描述

class Solution {public void flatten(TreeNode root) {if (root == null) {return;}Deque<TreeNode> stack = new LinkedList<TreeNode>();stack.push(root);TreeNode prev = null;while (!stack.isEmpty()) {TreeNode curr = stack.pop();if (prev != null) {prev.left = null;prev.right = curr;}TreeNode left = curr.left, right = curr.right;//先右后左if (right != null) {stack.push(right);}if (left != null) {stack.push(left);}prev = curr;}}
}

3. 前驱节点

前两种方法都借助前序遍历，前序遍历过程中需要使用栈存储节点。有没有空间复杂度是 O(1)O(1) 的做法呢？

注意到前序遍历访问各节点的顺序是根节点、左子树、右子树。如果一个节点的左子节点为空，则该节点不需要进行展开操作。如果一个节点的左子节点不为空，则该节点的左子树中的最后一个节点被访问之后，该节点的右子节点被访问。该节点的左子树中最后一个被访问的节点是左子树中的最右边的节点，也是该节点的前驱节点。因此，问题转化成寻找当前节点的前驱节点。

步骤
对于当前节点，如果其左子节点不为空，则在其左子树中找到最右边的节点，作为前驱节点，将当前节点的右子节点赋给前驱节点的右子节点，然后将当前节点的左子节点赋给当前节点的右子节点，并将当前节点的左子节点设为空。对当前节点处理结束后，继续处理链表中的下一个节点，直到所有节点都处理结束。

时间复杂度：O(N) 空间复杂度：O(1)
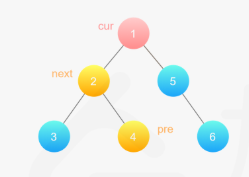
在这里插入图片描述

class Solution {public void flatten(TreeNode root) {TreeNode curr = root;while (curr != null) {if (curr.left != null) {TreeNode next = curr.left;TreeNode predecessor = next;while (predecessor.right != null) {predecessor = predecessor.right;}predecessor.right = curr.right;curr.left = null;curr.right = next;}curr = curr.right;}}
}

递归写法

    1/ \2   5/ \   \
3   4   6//将 1 的左子树插入到右子树的地方1\2         5/ \         \3   4         6        
//将原来的右子树接到左子树的最右边节点1\2          / \          3   4  \5\6//将 2 的左子树插入到右子树的地方1\2          \          3       4  \5\6   //将原来的右子树接到左子树的最右边节点1\2          \          3      \4  \5\6

递归版本
在这里插入图片描述

相应的左孩子也要置为 null，同样的也不用担心左孩子丢失，因为是后序遍历，左孩子已经遍历过了

private TreeNode pre = null;public void flatten(TreeNode root) {if (root == null)return;flatten(root.right);flatten(root.left);root.right = pre;root.left = null;pre = root;
}

【总结】

1. 解法一二自顶向下解法三自底向上

2.List接口常用方法

// 1、将指定的元素,添加到该集合中的指定位置上。
public void add(int index, E element)// 2、返回集合中指定位置的元素。
public E get(int index)// 3、移除列表中指定位置的元素,返回的是被移除的元素。
public E remove(int index)// 4、用指定元素替换集合中指定位置的元素,返回值的更新前的元素。
public E set(int index, E element)