本章记录
　1二元随机变量的定义
　2二元离散型随机变量的定义、联合概率分布律、边际分布律、条件分布律
　3二元离散型随机变量联合概率分布律函数、边际分布函数、条件分布函数
　4二元连续型随机变量的定义、联合概率密度函数、边际密度函数、条件密度函数
二元随机变量
　举例：研究入学儿童的发育情况。从一个样本（儿童）的身高、体重，两个维度研究。这用面向对象的编程角度理解类似于一个实体，有两个属性。
　再个栗子：研究炮弹着点位置。每个样本（位置）由横坐标、纵坐标确定。
　这两个例子中每个样本的两个维度不是固定不变的，而是随机变化的。入学儿童的年龄在样本空间中就几乎不变（在我们国家入学年龄7岁），入学年龄就不是随机变量。
　定义：设E是一个随机试验，样本空间S={e}，设X=X{e}，Y=Y(e)是定义在S上的随机变量，由它们构成的向量(X,Y)称为二元随机变量，也称二维随机变量。

二元离散型随机变量
　定义：若二元随机变量（X,Y）全部可能取到不同的值是有限对，或者可列无数对，则称(X,Y)是二元离散型随机变量。
　
二元离散型随机变量的概率分布律
　定义：若(X,Y)所有可能取值为$(x_i,y_j)$称$P(X=x_i,Y=y_j)=p_{ij},i,j=1,2,3...$为二元离散型随机变量(X,Y)的联合概率分布律。也可简称(X,Y)的分布律。
　性质
　1 $p_{ij} \geq 0$。
　2 $\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} p_{ij}=1$
　3 $P((X,Y) \in D)=\sum_{x_i,y_j \in D} p_{ij}$，其中$p_{ij}=P(X=x_i,Y=y_j)，i,j=1,2,3...$
　举例
　

二元离散型随机变量的边际分布律
　定义：离散型随机变量(X,Y)的边际分布律为$P(X=x_i)=\sum_{j=1}^{\infty}p(x_i,y_j)$，记为$p_{i.}$，$P(Y=y_j)=\sum_{i=1}^{\infty}p(x_i,y_j)$，记为$p_{.j}$。
　

二元离散型随机变量的条件分布律
　定义：(X,Y)是二元离散型随机变量，对于固定的$y_j$，如果$P(Y=y_j)>0$(Y的边际分布律>0)，则称$P(X=x_i|Y=y_j)=\frac{P(X=x_i,Y=y_j)}{P(Y=y_j)}=\frac{p_{ij}}{p_{.j}}$，$i=i,2,3...$，为在$Y=y_j$条件下，随机变量X的条件分布律。
　同样的，对于固定的$x_i$，如果$P(X=x_i)>0$，则称$P(Y=y_j|X=x_i)=\frac{P(X=x_i,Y=y_j)}{P(X=x_i)}=\frac{p_{ij}}{p_{i.}}$，$j=i,2,3...$，为在$X=x_i$条件下，随机变量Y的条件分布律。
　例子
　
　
　
　
　
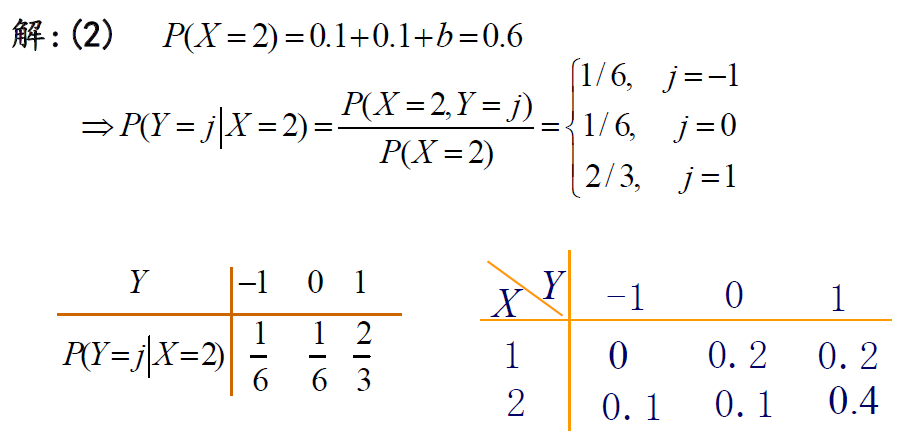
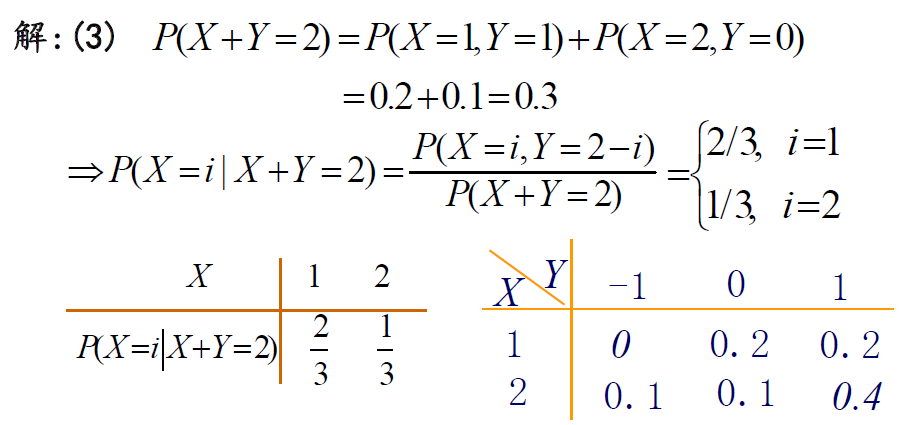
二元随机变量的联合分布函数
　定义：若(X,Y)是二元随机变量，对于任意的实数x,y二元函数$F(x,y)=P(X\leq x,Y\leq y)$，称为二元随机变量(X,Y)的联合分布函数。
　二元离散型随机变量的联合分布函数:$F(x,y)=P(X \leq x,Y\leq y)=\sum_{x_i \leq x,y_j \leq y}P(X=x_i,Y=y_j)$。
　性质：
　1 F(x,y)关于x,y单调不递减。
　2 $0 \leq F(x,y) \leq 1$，$F(-\infty,+\infty)=1$
　3 F(x,y)关于x,y右连续，即 $\lim _{\varepsilon \rightarrow 0^{+}}F\left( x+\varepsilon ,y\right)=F(x,y)$，$\lim _{\varepsilon \rightarrow 0^{+}}F\left( x ,y+\varepsilon \right)=F(x,y)$
　4 如果$x_1<x<x_2，y_1<y<y_2$则有
　$P(x_1<X\leq x_2,y_1<Y \leq y_2)=F(x_2,y_2)-F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1)$
　

二元随机变量的边际分布函数
　定义：二元随机变量(X,Y)关于X的边际分布函数记为$F_X(x)$，关于Y的边际分布函数记为$F_Y(y)$。
　$F_X(x)=P(X\leq x)=P(X\leq x,Y<+\infty)=F(x,+\infty)=lim_{y \rightarrow +\infty F(x,y)}$
　$F_Y(y)=P(Y\leq y)=P(X<+\infty,Y\leq y,)=F(+\infty,y)=lim_{x \rightarrow +\infty F(x,y)}$

二元随机变量的条件分布函数
　定义：如果$P(Y=y)>0$，则在Y=y条件下，X的条件分布函数为$F_{X|Y}(x|y)=P(X\leq x|Y= y)=\frac{P(X\leq x,Y=y)}{P(Y=y)}$，如果(X,Y)是离散型随机变量，则$P(Y=y)>0$。
　如果(X,Y)是连续型随机变量，P(Y=y)=0，但是$\varepsilon >0,P(y<Y<y+\varepsilon)>0$，则在Y=y 条件下X的条件分布函数定义为$F_{X|Y}(x|y)=lim_{\varepsilon \rightarrow 0^+}P(X\leq x|y<Y<y+\varepsilon)$

二元连续型随机变量
　定义：对于二元随机变量(X,Y)的分布函数F(x,y)，如果存在非负函数f(x,y)，使得对于任意x,y 有$F(x,y)=\int_{-\infty}^{x}\int_{-\infty}^{y} f(u,v)dudv$，称(X,Y)为二元连续型随机变量，称f(x,y)为二元随机变量(X,Y)的联合概率密度函数。
　
二元连续型随机变量联合概率密度函数
　性质
　1 f(x,y)>=0
　2 $\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f(x,y)dxdy=1$，在几何上z=f(x,y)表示空间的一个顶曲面，介于它和x0y平面的空间体积为1。
　3 概率和。设D是xoy平面上的区域，点(X,Y)落在D内的概率为$P((X,Y) \in D)=\int \int_D f(x,y)dxdy$。$P((X,Y) \in D)$等于以D为底，曲面f(x,y)为顶面的柱体体积。
　4 在f(x,y)的连续点(x,y)，有F(x,y)的二阶导=f(x,y)
　二元连续型随机变量的概率密度函数与分布函数之间就是积分与求导的关系了。

二元连续型随机变量边际概率密度函数
　定义：对于连续型随机变量(X,Y)，概率密度函数为f(x,y)，X,Y的边际概率密度函数为：
　$f_X(x)=\int_{-\infty}^{+\infty}f(x,y)dy$
　$f_Y(y)=\int_{-\infty}^{+\infty}f(x,y)dx$
　要注意 对x积分的时候，y是不变的，x的边界是：要找到 x自己的边界以及与y的关系边界的交集。对y积分的时候也一样。
二元连续型随机变量条件概率密度函数
　定义：设二元随机变量(X,Y)的概率密度为f(x,y)，(X,Y)关于Y的边际概率密度函数$f_Y(y)$，若对于固定的y，$f_Y(y)>0$且$f_Y(y)$是连续的，则在Y=y的条件下，X的条件概率密度为：$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$。
　同理，若对于固定的X=x，且$f_X(x)$连续的，在X=x的条件下，Y的条件概率密度为$f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)}$。
　
　
二元均匀分布
　定义：如果二元随机变量(X,Y)的概率密度函数在平面上的一个有界区域D内是常数，而在其他地方取值为0，则称(X,Y)在D上服从均匀分布。
　$f\left( x,y\right) =\begin{cases} \dfrac {1} {A},\left( x,y\right) \in D\\ 0,other\end{cases}$
　A=D，也就是说在D上，f(x,y)=1/面积。
　二元均匀分布的条件分布仍然是均匀分布。
二元正态分布

　二元正态分布的两个边际分布函数都是一元正态分布，并且与$\rho$没有关系。在X=x的条件下，Y的条件分布也是正态分布。