链接:https://www.zhihu.com/question/26665048/answer/157852228
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
马尔可夫链 (Markov Chain)是什么鬼
它是随机过程中的一种过程,一个统计模型,到底是哪一种过程呢?好像一两句话也说不清楚,还是先看个例子吧。
先说说我们村智商为0的王二狗,人傻不拉几的,见人就傻笑,每天中午12点的标配,仨状态:吃,玩,睡。这就是传说中的状态分布。

你想知道他n天后中午12点的状态么?是在吃,还是在玩,还是在睡?这些状态发生的概率分别都是多少? (知道你不想,就假装想知道吧~~学习真的好累~~)
先看个假设,他每个状态的转移都是有概率的,比如今天玩,明天睡的概率是几,今天玩,明天也玩的概率是几几,还是先看个图吧,更直观一些。

这个矩阵就是转移概率矩阵P,并且它是保持不变的,就是说第一天到第二天的转移概率矩阵跟第二天到第三天的转移概率矩阵是一样的。(这个叫时齐,不细说了,有兴趣的同学自行百度)。
有了这个矩阵,再加上已知的第一天的状态分布,就可以计算出第N天的状态分布了。

S1 是4月1号中午12点的的状态分布矩阵 [0.6, 0.2, 0.2],里面的数字分别代表吃的概率,玩的概率,睡的概率。
那么
4月2号的状态分布矩阵 S2 = S1 * P (俩矩阵相乘)。
4月3号的状态分布矩阵 S3 = S2 * P (看见没,跟S1无关,只跟S2有关)。
4月4号的状态分布矩阵 S4 = S3 * P (看见没,跟S1,S2无关,只跟S3有关)。
...
4月n号的状态分布矩阵 Sn = Sn-1 * P (看见没,只跟它前面一个状态Sn-1有关)。
-------------------------------------------------------------------------------------------------------------------------
总结:马尔可夫链就是这样一个任性的过程,它将来的状态分布只取决于现在,跟过去无关!
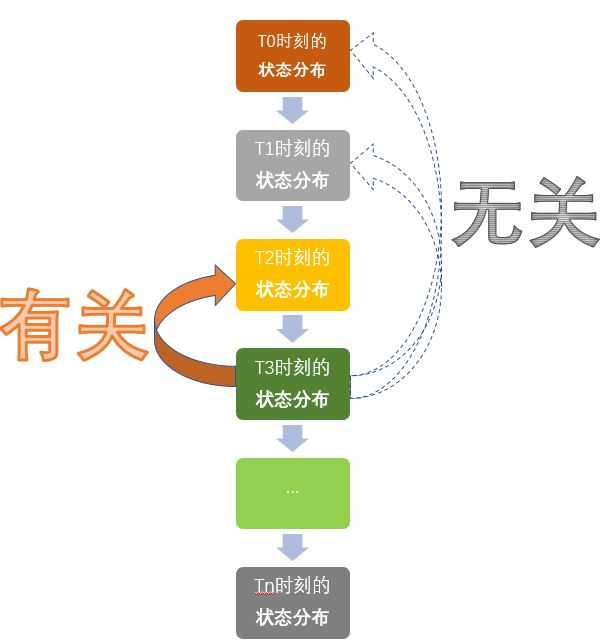
就把下面这幅图想象成是一个马尔可夫链吧。实际上就是一个随机变量随时间按照Markov性质进行变化的过程。
-----------------------------更新-------------------------------
有人问到 S2 的计算过程,那我就贴上来吧,不关心的同学可以忽略。
这是我手写的计算过程。
科学中的应用
马尔可夫链通常用来建模排队理论和统计学中的建模,还可作为信号模型用于熵编码技术,如算法编码。马尔可夫链也有众多的生物学应用,特别是人口过程,可以帮助模拟生物人口过程的建模。隐蔽马尔可夫模型还被用于生物信息学,用以编码区域或基因预测。
马尔可夫链最近的应用是在地理统计学(geostatistics)中。其中,马尔可夫链用在基于观察数据的二到三维离散变量的随机模拟。这一应用类似于“克里金”地理统计学(Kriging geostatistics),被称为是“马尔可夫链地理统计学”。这一马尔可夫链地理统计学方法仍在发展过程中。
马尔可夫链模型主要是分析一个人在某一阶段内由一个职位调到另一个职位的可能性,即调动的概率。该模型的一个基本假设就是,过去的内部人事变动的模式和概率与未来的趋势大体相一致。实际上,这种方法是要分析企业内部人力资源的流动趋势和概率,如升迁、转职、调配或离职等方面的情况,以便为内部的人力资源的调配提供依据。
它的基本思想是:通过发现过去组织人事变动的规律,以推测组织在未来人员的供给情况。马尔可夫链模型通常是分几个时期收集数据,然后再得出平均值,用这些数据代表每一种职位中人员变动的频率,就可以推测出人员变动情况。
具体做法是:将计划初期每一种工作的人数量与每一种工作的人员变动概率相乘,然后纵向相加,即得到组织内部未来劳动力的净供给量。其基本表达式为:
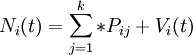
- Ni(t):t时间内I类人员数量;
- Pji:人员从j类向I类转移的转移率;
- Vi(t):在时间(t-1,t)I类所补充的人员数。
企业人员的变动有调出、调入、平调、晋升与降级五种。表3 假设一家零售公司在1999至2000年间各类人员的变动情况。年初商店经理有12人,在当年期间平均90%的商店经理仍在商店内,10%的商店经理离职,期初36位经理助理有 11%晋升到经理,83%留在原来的职务,6%离职;如果人员的变动频率是相对稳定的,那么在2000年留在经理职位上有11人(12×90%),另外,经理助理中有4人(36×83%)晋升到经理职位,最后经理的总数是15人(11+4)。可以根据这一矩阵得到其他人员的供给情况,也可以计算出其后各个时期的预测结果。假设的零售公司的马尔可夫分析,见下表:
| 1999~2000 | 商店经理 | 经理助理 | 区域经理 | 部门经理 | 销售员 | 离职 |
|---|---|---|---|---|---|---|
| 商店经理 (n=12) | 90% 11 | 10% 1 | ||||
| 经理助理 (n=36) | 11% 4 | 83% 30 | 6% 2 | |||
| 区域经理 (n=96) | 11% 11 | 66% 63 | 8% 8 | 15% 14 | ||
| 部门经理 (=288) | 10% 29 | 72% 207 | 2% 6 | 16% 46 | ||
| 销售员 (=1440) | 6% 86 | 74% 1066 | 25% 228 | |||
| 供给预测 | 15 | 41 | 92 | 301 | 1072 | 351 |