C#中字段、属性和构造函数赋值的问题

提出问题

首先提出几个问题：

1、如何实现自己的注入框架？

2、字段和自动属性的区别是什么？

3、字段和自动属性声明时的直接赋值和构造函数赋值有什么区别？

4、为什么只读字段和只读自动属性（只有get没有set访问器）都可以在构造函数中进行赋值？

5、反射可以给只读字段或者只读属性进行赋值吗？

6、自动属性和普通属性的区别？

这些问题是我在试着写自己的注入实现时遇到的问题。这些问题应该在学习C#时的第一节课就应该学到了，我看网上还有人分享说他在面试时遇到面试官问为什么只读字段和只读自动属性可以在构造函数中进行赋值，他没有回答上来，然后他写文章探讨这个问题，却没有得出一个明显的答案，实在可惜。网上关于只读属性有些是写ReadOnly特性的，读到这些文章直接跳过吧，老版本的C#现在看也没什么帮助。

给出答案

2、属性比字段多了get/set访问器；字段是在内存中声明的一个内存空间，可以实实在在的存储值；属性像字段一样使用，却可以有自己的代码段，能赋值取值，是因为访问属性就是调用属性的get/set方法对字段进行取值赋值（或者不操作字段）；在MSDN上，建议字段作为类的私有变量使用private/protected修饰，属性则往往作为共有属性使用public修饰；字段的读取和操作都是直接操作内存，属性是调用get/set访问器，所以字段比属性快。

3、准确来说，没有区别。区别仅仅是直接赋值先执行，构造函数赋值后执行。在生成的IL中间语言（C#代码先编译成IL代码，然后才编译成汇编语言）中，字段直接赋值和构造函数赋值是在同一个代码段中（构造函数中）的。

4、这个问题可以和上面的问题联合起来回答。构造函数作为实例化一个类的入口，是最先访问的。字段的直接赋值其实也是放在构造函数中执行的，所以才说直接赋值和构造函数赋值没有区别。“只读”的限制只是由C#编译器（CLR）维护的，我觉得全名应该叫做“除构造函数外只读”更加准确，这是C#语法的规则记住就行（这是当然，直接赋值其实是放在构造函数中进行赋值的，如果构造函数不能赋值那只读字段没有值和没有声明一样）；

5、这个问题又可以和上面的问题联系起来一起回答。通过反射可以给自读字段赋值但是无法给只读属性进行赋值（不相信的可以试一下）。对只读字段的赋值是因为绕过了C#编译器（CLR）的只读显示，对只读属性赋值的话是还是调用set访问器对字段进行赋值，因为没有set访问器所以允许后会报错。那么问题来了，那为什么只读自动属性没有set访问器还可以在构造函数中赋值呢？其实只读自动属性在构造函数中进行赋值，实质上是对字段进行赋值，和属性的get/set访问器没有关系。

6、区别是什么？上面一直强调自动属性，是因为自动属性和普通属性不一样，比如只读普通属性（没有set访问器）无法在构造函数中赋值。在没有自动属性之前，普通属性使用步骤是首先声明一个字段如_id，然后声明一个属性Id，在get和set访问器中做一些操作，这些操作大多数是对字段_id的操作，但是有时候和字段没有关系。普通属性可以像字段一样通过“.”的方式调用，但又像方法一样具有代码段（普通属性从来不开辟内存空间）。

但是C#3.0之后引入了自动属性，声明方式如public int id { get; set; }，C#6.0之后又有了public string FirstName { get; set; } = "Jane"。自动属性肯定开辟了内存空间然后才有了自动属性的直接赋值。其实在类中声明自动属性会在编译成IL中间语言中声明一个隐藏字段，然后生成隐藏字段的get/set方法，然后生成get/set访问器。这里可以解释为什么只读普通属性无法在构造函数中赋值（和直接赋值）而只读自动属性可以在构造函数中赋值（和直接赋值），因为不论直接赋值还是在构造函数中赋值，生成的IL代码中的构造函数中，操作的都是隐藏字段，并没有访问属性的set访问器。（注意这里只是说的类中的自动属性，接口中也是可以有自动属性的，但是接口的自动属性并不会生成隐藏字段只是定义get/set访问器）

开始解释

通过C#生成的IL中间语言代码可以知道的更清楚

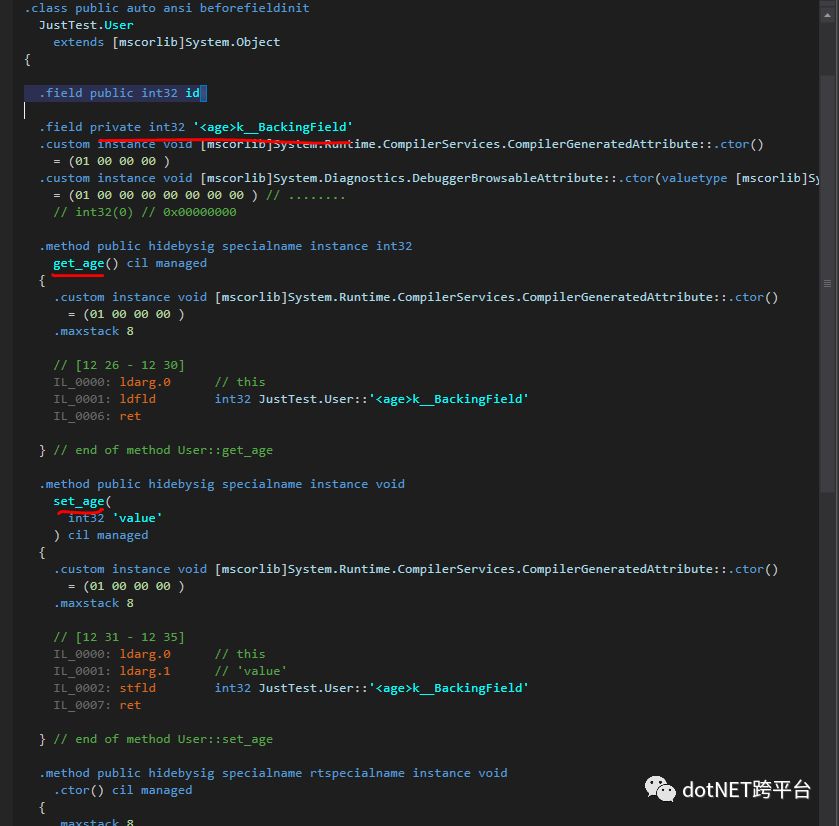
可以看到，自动属性会生成一个名称为 '<age>k__BackingField' 的隐藏私有字段+私有字段的get/set方法+属性代码段；

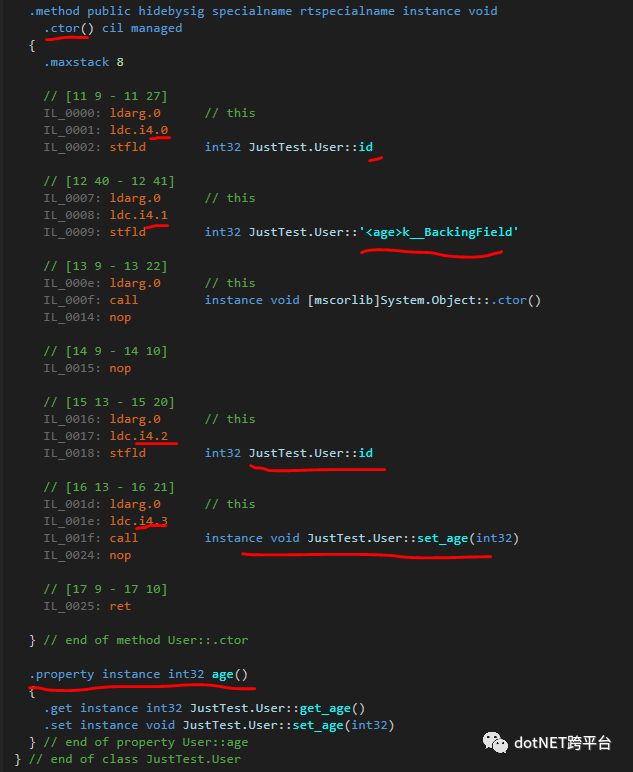
可以看到IL代码生成了User的构造函数 .ctor，ctor是构造函数（Constructor）。

不论直接赋值还是构造函数赋值，都是在.ctor中执行的，并且操作的都是字段，自动属性的赋值操作的是隐藏字段。

  public interface IUser{    int id { get; set; }}

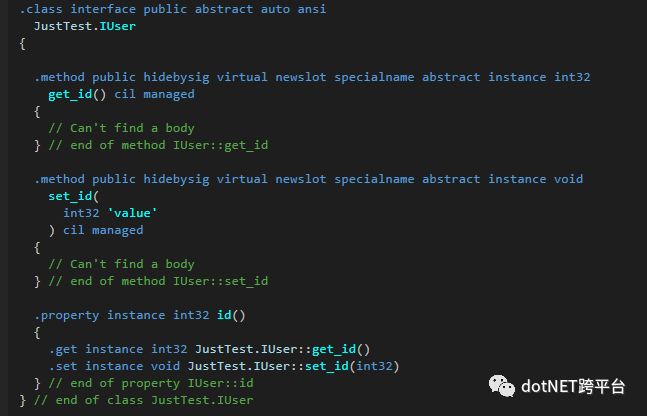
可以看到，接口中的自动属性并没有生成隐藏字段。

其他说明

1、上文中提到“反射可以给只读字段进行赋值但是无法给只读属性进行赋值”。无法给只读属性进行赋值是因为没有set访问器。但是我们已经知道了可以给字段赋值，并且只读属性会生成隐藏字段，那我们是不是可以通过给隐藏字段进行赋值间接达到给自动属性赋值的目的呢？答案是可以的！

定义User的只读自动属性

控制台的反射赋值代码：

运行

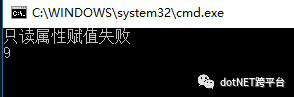
2、因为隐藏字段是私有的，所以取到隐藏字段需要  BindingFlags.NonPublic

3、只读自动属性说明不想被访问到那为什么还要给它赋值呢？这个问题……做着玩，项目中我觉得也没有什么用到的机会……

原文地址：https://www.cnblogs.com/gdpw/p/9463145.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com