牛客网
题目描述

作为体育委员，C君负责这次运动会仪仗队的训练。 仪仗队是由学生组成的N *
N的方阵，为了保证队伍在行进中整齐划一，C君会跟在仪仗队的左后方，根据其视线所及的学生人数来判断队伍是否整齐(如下图)。

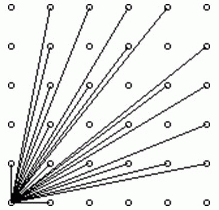
现在，C君希望你告诉他队伍整齐时能看到的学生人数。
输入描述:

共一个数N。

输出描述:

共一个数，即C君应看到的学生人数。

示例1
输入

4

输出

9

题解：
无限接近裸的欧拉函数
可以自己画图看看
我来解释下我这个图，我把n=4和5画在了一起，紫色区域是44区域，红色区域（也是整个区域）是55，左上角围成一个三角形区域，我们暂时不考虑对角线上的情况（因为对角线只能看见一个，后面的都被挡住了）。
左下角坐标是（0,0），我们发现能看的坐标（x，y），x与y为互质，如果不是互质，就一定会被挡住，（比如（2,4）会被（1,2）挡住，而1与2互质，（1,2）就不会被挡住）
我们用ans记录三角区域的情况数
就是ans=每行的情况加一起
那每行有多少种，可以用欧拉函数求
欧拉函数的ϕ(x)表示小于x的且与x互质的数有多少个
ϕ(3)=2（与3互质的有1和2，一共有两个）
特别注意ϕ(1)=1
公式法：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e4+10;
int n, phi[maxn];
// 直接求3
long long Euler( long long n ){long long res = n;for( long long i =2 ;i*i<=n;i++){if( n %i == 0 ){n/=i;res = res - res/i;}while( n % i==0)n/=i;}if( n > 1 )res = res - res/n;return res;
}int main() {scanf("%d", &n);int ans = 0;for(int i = 1; i < n; i++) ans += Euler(i);printf("%d", ans * 2 + 1);return 0;
}

筛法：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e4+10;
int n, phi[maxn];
void get_phi(int n) {phi[1] = 1;for(int i = 2; i <= n; i++) if(!phi[i]) {for(int j = i; j <= n; j += i) {if(!phi[j]) phi[j] = j;phi[j] = phi[j] / i * (i-1);}}
}
int main() {scanf("%d", &n);get_phi(n);int ans = 0;for(int i = 1; i < n; i++) ans += phi[i];printf("%d", ans * 2 + 1);return 0;
}

---

记录下欧拉函数的模板：
筛法：

/*
特性 :
1.若a为质数,phi[a]=a-1;
2.若a为质数,b mod a=0,phi[a*b]=phi[b]*a
3.若a,b互质,phi[a*b]=phi[a]*phi[b](当a为质数时,if b mod a!=0 ,phi[a*b]=phi[a]*phi[b])
*/
int m[n],phi[n],p[n],nump;
//m[i]标记i是否为素数,0为素数,1不为素数;p是存放素数的数组;nump是当前素数个数;phi[i]为欧拉函数
int calc()
{phi[1]=1;for (int i=2;i<=n;i++){if (!m[i])//i为素数{p[++nump]=i;//将i加入素数数组p中phi[i]=i-1;//因为i是素数,由特性得知    }    for (int j=1;j<=nump&&p[j]*i<n;j++)  //用当前已的到的素数数组p筛,筛去p[j]*i{m[p[j]*i]=1;//可以确定i*p[j]不是素数 if (i%p[j]==0) //看p[j]是否是i的约数,因为素数p[j],等于判断i和p[j]是否互质 {phi[p[j]*i]=phi[i]*p[j]; //特性2break;}else phi[p[j]*i]=phi[i]*(p[j]-1); //互质,特性3其,p[j]-1就是phi[p[j]]   }}
}

公式法：

//1
int eular(int n)
{int ret=1,i;for(i=2;i*i<=n;i++){if(n%i==0){n/=i,ret*=i-1;while(n%i==0) n/=i,ret*=i;}}if(n>1) ret*=n-1;return ret;
}
// 2
int Phi(int N) {int m = (int)sqrt(N + 0.5), ans = N;for(int i=2; i<=m; i++)if(N % i == 0) {ans = ans / i * (i-1);while(N % i == 0) N /= i;}if(N > 1) ans = ans / N * (N-1);return ans;
}