本文主要是对.NET Core开发日志——Middleware的补遗，但是会从看起来平平无奇的RequestDelegate开始叙述，所以以其作为标题，也是合情合理。

RequestDelegate是一种委托类型，其全貌为public delegate Task RequestDelegate(HttpContext context)，MSDN上对它的解释，"A function that can process an HTTP request."——处理HTTP请求的函数。唯一参数，是最熟悉不过的HttpContext，返回值则是表示请求处理完成的异步操作类型。

可以将其理解为ASP.NET Core中对一切HTTP请求处理的抽象(委托类型本身可视为函数模板，其实现具有统一的参数列表及返回值类型)，没有它整个框架就失去了对HTTP请求的处理能力。

并且它也是构成Middleware的基石。或者更准确地说参数与返回值都是其的Func<RequestDelegate, RequestDelegate>委托类型正是维持Middleware运转的核心齿轮。

组装齿轮的地方位于ApplicationBuilder类之内，其中包含着所有齿轮的集合。

private readonly IList<Func<RequestDelegate, RequestDelegate>> _components = new List<Func<RequestDelegate, RequestDelegate>>();

以及添加齿轮的方法：

在Startup类的Configure方法里调用以上ApplicationBuilder的Use方法，就可以完成一个最简单的Middleware。

齿轮要想变成Middleware，在完成添加后，还需要经过组装。

Build方法里先定义了最底层的零件——app，context => { 

context.Response.StatusCode = 404; 

return Task.CompletedTask; }，

这段代码意味着，如果没有添加任何Middleware的话，ASP.NET Core站点启动后，会直接出现404的错误。

接下的一段，遍历倒序排列的齿轮，开始正式组装。

在上述例子里，只使用了一个齿轮：

那么第一次也是最后一次循环后，执行component(app)操作，app被重新赋值为：

context => context.Response.WriteAsync("Hello, World!");

组装的结果便是app的值。

这个组装过程在WebHost进行BuildApplication时开始操作。从此方法的返回值类型可以看出，虽然明义上是创建Application，其实生成的是RequestDelegate。

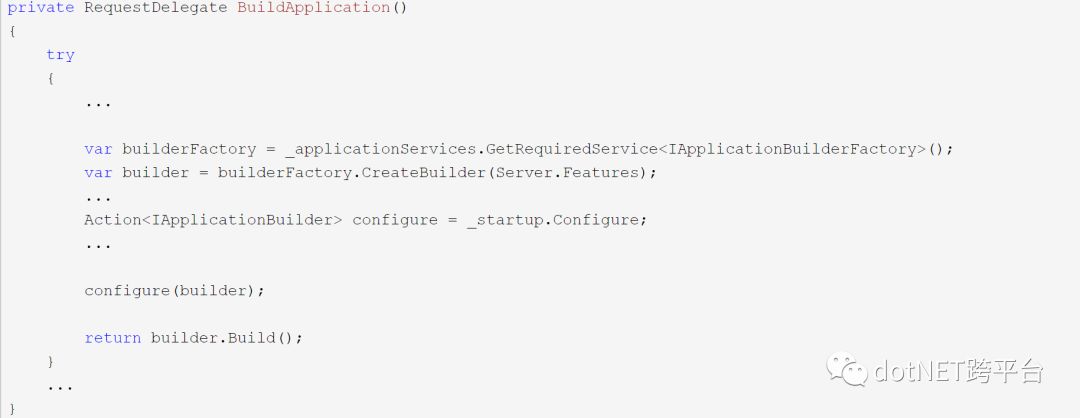
而这个RequestDelegate最终会在HostingApplication类的ProcessRequestAsync方法里被调用。

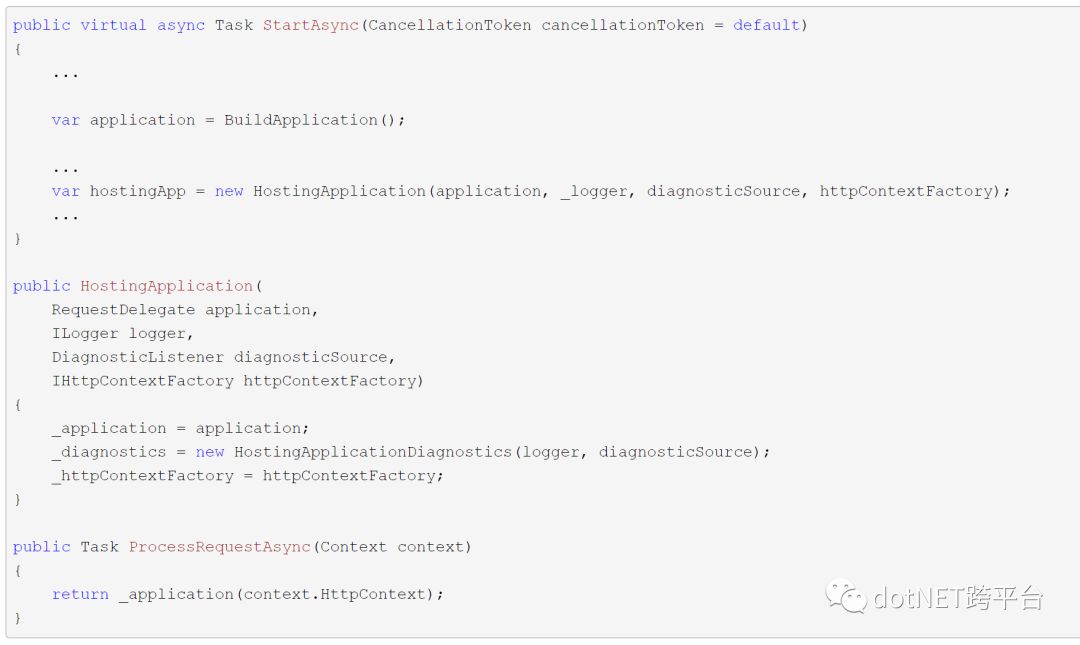
上例中的执行结果即是显示Hello, World!字符。

404的错误不再出现，意味着这种Middleware只会完成自己对HTTP请求的处理，并不会将请求传至下一层的Middleware。

要想达成不断传递请求的目的，需要使用另一种Use扩展方法。

在实际代码中可以这么写：

现在多了个Middleware，继续上面的组装过程。app的值最终被赋值为：

显示结果为：

I am a Middleware!
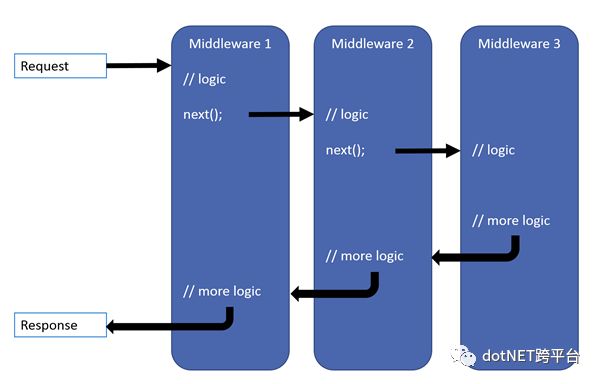
Hello, World!

下面的流程图中可以清楚地说明这个过程。

如果把await next.Invoke()注释掉的话，

上例中第一个Middleware处理完后，不会继续交给第二个Middleware处理。注意以下simpleNext的方法只被定义而没有被调用。

这种情况被称为短路(short-circuiting)。

做短路处理的Middleware一般会放在所有Middleware的最后，以作为整个pipeline的终点。

并且更常见的方式是用Run扩展方法。

所以可以把上面例子的代码改成下面的形式：

除了短路之外，Middleware处理时还可以有分支的情况。

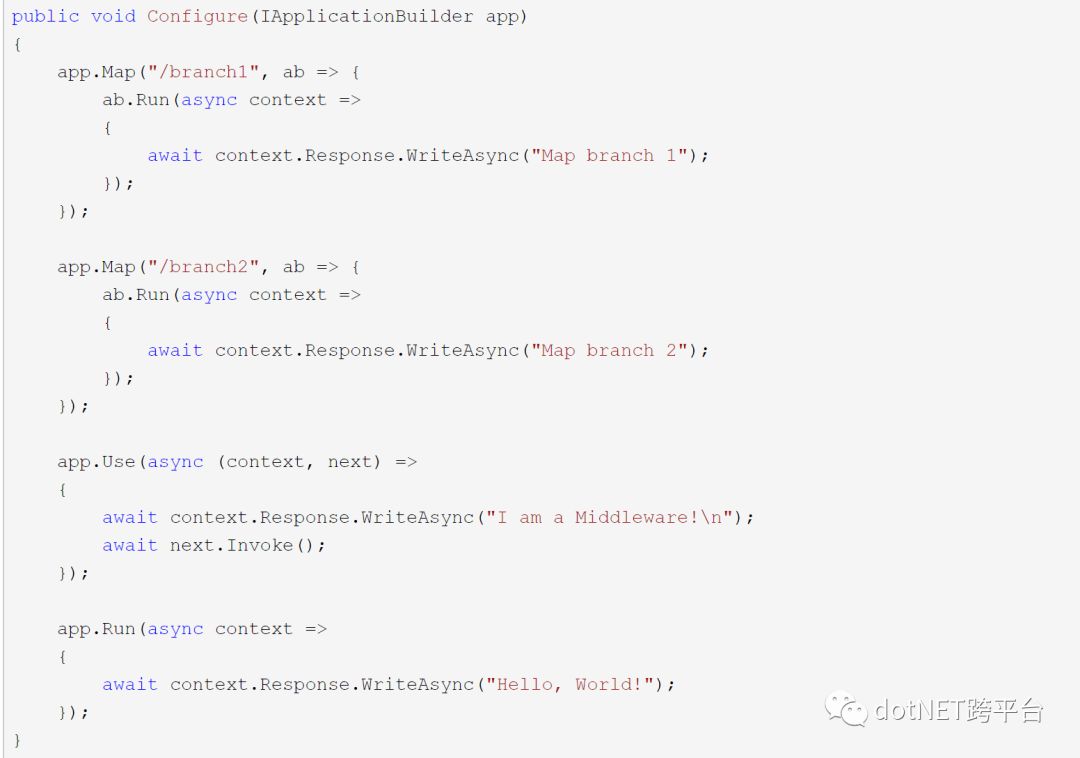
URL地址后面跟着branch1时：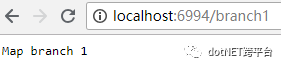

URL地址后面跟着branch2时：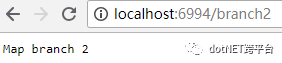

其它情况下：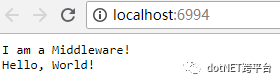

Map扩展方法的代码实现：

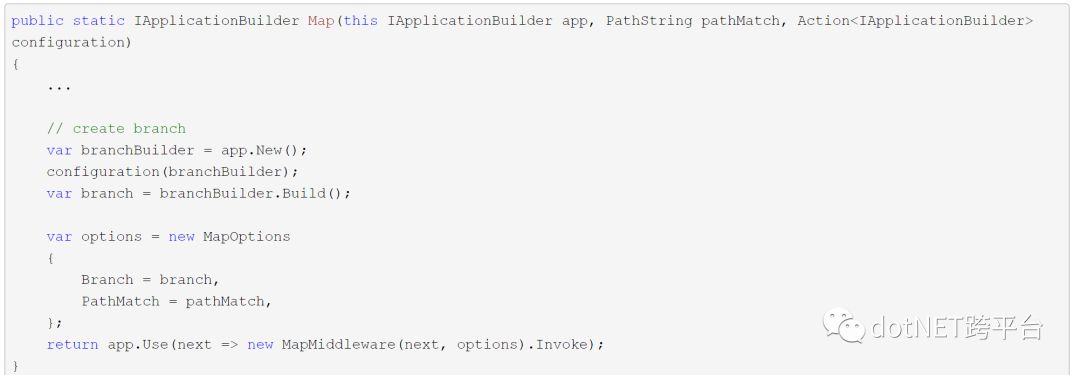
创建分支的办法就是重新实例化一个ApplicationBuilder。

public IApplicationBuilder New(){   
      return new ApplicationBuilder(this);
}

对分支的处理则是封装在MapMiddleware类之中。

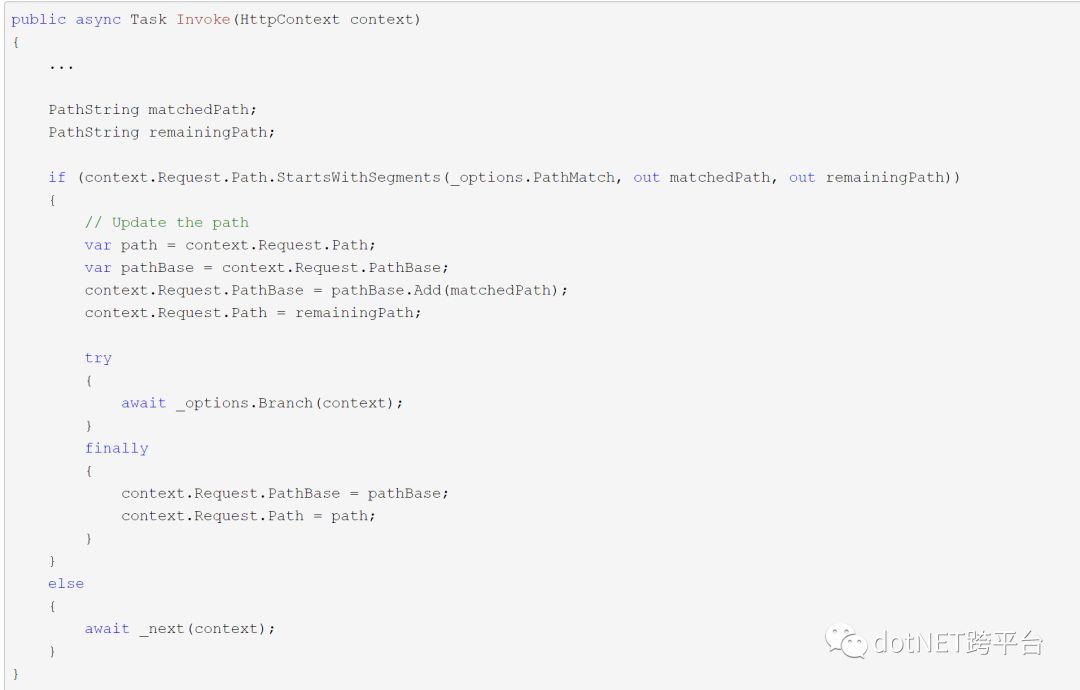
说到MapMiddleware，不得不提及各种以Use开头的扩展方法，比如UseStaticFiles，UseMvc，UsePathBase等等。

这些方法内部都会调用UseMiddleware方法以使用各类定制的Middleware类。如下面UsePathBase的代码：

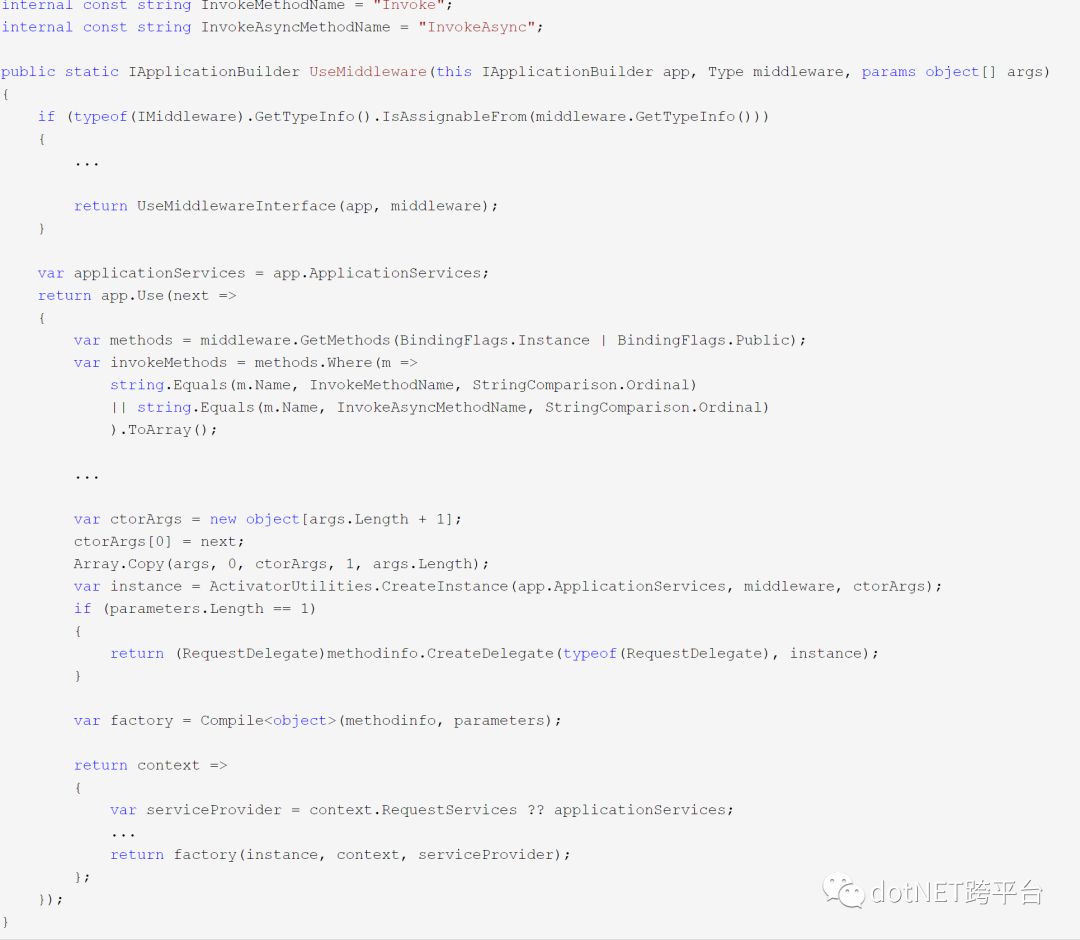
而从UseMiddleware方法中可以获知，Middleware类需满足两者条件之一才能被有效使用。其一是实现IMiddleware，其二，必须有Invoke或者InvokeAsync方法，且方法至少要有一个HttpContext类型参数(它还只能是放第一个)，同时返回值需要是Task类型。

对ASP.NET Core中Middleware的介绍到此终于可以告一段落，希望这两篇文章能够为读者提供些许助力。

原文地址：https://www.cnblogs.com/kenwoo/p/9404671.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com