一直以来,我以为 LINQ 是专门用来对不同数据源进行查询的工具,直到我看了这篇十多年前的文章,才发现 LINQ 的功能远不止 Query。这篇文章的内容比较高级,主要写了用 C# 3.0 推出的 LINQ 语法实现了一套“解析器组合子(Parser Combinator)”的过程。那么这个组合子是用来干什么的呢?简单来说,就是把一个个小型的语法解析器组装成一个大的语法解析器。当然了,我本身水平有限,暂时还写不出来这么高级的代码,不过这篇文章中的一段话引起了我的注意:
Any type which implements Select, SelectMany and Where methods supports (part of) the "query pattern" which means we can write C#3.0 queries including multiple froms, an optional where clause and a select clause to process objects of this type.
大意就是,任何实现了 Select,SelectMany 等方法的类型,都是支持类似于 from x in y select x.z 这样的 LINQ 语法的。比如说,如果我们为 Task 类型实现了上面提到的两个方法,那么我们就可以不借助 async/await 来对 Task 进行操作:

那么我们就来看看如何实现一个非常简单的 LINQ to Task 吧。
LINQ to Task
首先我们要定义一个 Select 拓展方法,用来实现通过一个 Func<TValue, TResult> 将 Task<TValue> 转换成 Task<TResult> 的功能。
static async Task<TR> Select<TV,TR>(this Task<TV> task, Func<TV, TR> selector) { var value = await task; // 取出 task 中的值return selector(value); // 使用 selector 对取出的值进行变换}这个函数非常简单,甚至可以简化为一行代码,不过仅仅这是这样就可以让我们写出一个非常简单的 LINQ 语句了:
var taskA = Task.FromResult(12);var r = from a in taskA select a * a;那么实际上 C# 编译器是如何工作的呢?我们可以借助下面这个有趣的函数来一探究竟:
void PrintExpr<T1,T2>(Expression<Func<T1, T2>> expr) {Console.WriteLine(expr.ToString());
}熟悉 LINQ 的人肯定对 Expression 不陌生,Expressing 给了我们在运行时解析代码结构的能力。在 C# 里面,我们可以非常轻松地把一个 Lambda 转换成一个 Expression,然后调用转换后的 Expression 对象的 ToString() 方法,我们就可以在运行时以字符串的形式获取到 Lambda 的源码。例如:
var taskA = Task.FromResult(12);
PrintExpr((int _) => from a in taskA select a * a);// 输出: _ => taskA.Select(a => (a * a))可以看到,Expression 把这段 LINQ 的真面目给我们揭示出来了。那么,更加复杂一点的 LINQ 呢?

如果你尝试运行这段代码,你应该会遇到一个错误——缺少对应的 SelectMany 方法,下面给出的就是这个 SelectMany 方法的实现:

这个 SelectMany 实现的功能就是,通过一个 Func<TValue, Task<TResult>> 将 Task<TValue> 转换成 Task<TResult>。有了这个之后,你就可以看到上面的那个较为复杂的 LINQ to Task 语句编译后的结果:
_ => taskA.SelectMany(a => taskB, (a, b) => (a * b))可以看到,当出现了两个 Task 之后,LINQ 就会使用 SelectMany 来代替 Select。可是我想为什么 LINQ 不像之前那样,用两个 Select 分别处理两个 Task 呢?为了弄清楚这个问题,我试着推导了一番:

结果比 LINQ 还多调用了两次 Select。仔细看的话,就会发现,我们所写的第二个 Select 其实就是 SelectMany,的第二个参数,而对于第一个 Select 来说,因为 b 是一个 Task,所以 b.Select(xxx) 的返回值肯定是一个 Task,而这又恰好符合 SelectMany 函数的第一个参数的特征。
有了上面的经验,我们不难推断出,当 from x in y 语句的个数超过 2 个的时候,LINQ 仍然会只使用 SelectMany 来进行翻译。因为 SelectMany可以被看作为把两层 Task 转换成单层 Task,例如:
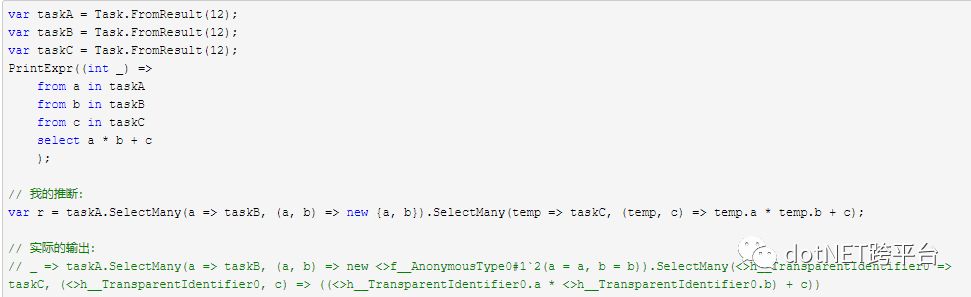
这里 LINQ 为第一个 SelectMany 的结果生成了一个匿名的中间类型,将 taskA 跟 taskB 的结果组合成了 Task<{a, b}>,方便在第二个 SelectMany 中使用。
至此,一个非常简单的 LINQ to Task 就完成了,通过这个小工具,我们可以实现不使用 async/await 就对类型进行操作。然而这并没有什么卵用,因为 async/await 确实要比 from x in y 这种语法要来的更加简单。不过举一反三,我们可以根据上面的经验来实现一个更加使用的小功能。
LINQ to Result
在一些比较函数式的语言(如 F#,Rust)中,会使用一种叫做 Result<TValue, TError> 的类型来进行异常处理。这个类型通常用来描述一个操作结果以及错误信息,帮助我们远离 Exception 的同时,还能保证我们全面的处理可能出现的错误。如果使用 C# 实现的话,一个 Result 类型可以被这么来定义:

接着仿照上面为 Task 定义 LINQ 拓展方法,为了 Result 设计 Select 跟 SelectMany:

那么 LINQ to Result 在实际中的应用是什么样子的呢,接下来我用一个小例子来说明:
某公司为感谢广大新老用户对 “5 元 30 M”流量包的支持,准备给余额在 350 元用户的以上的用户送 10% 话费。但是呢,如果用户在收到赠送的话费后余额会超出 600 元,就不送话费了。

可以看到,使用 Result 能够让我们更加清晰地用代码描述业务逻辑,而且如果我们需要向现有流程中添加新的验证逻辑,只需要在合适地地方插入 from result in validate(xxx) 就可以了,换句话说,我们的代码变得更加“声明式”了。
函数式编程
细心的你可能已经发现了,不管是 LINQ to Task 还是 LINQ to Result,我们都使用了某种特殊的类型(如:Task,Result)对值进行了包装,然后编写了特定的拓展方法 —— SelectMany,为这种类型定义了一个重要的基本操作。在函数式编程的里面,我们把这种特殊的类型统称为“Monad”,所谓“Monad”,不过是自函子范畴上的半幺群而已。
范畴(Category)与函子(Functor)
在高中数学,我们学习了一个概念——集合,这是范畴的一种。
对于我们程序员来说,int 类型的全部实例构成了一个集合(范畴),如果我们为其定义了一些函数,而且它们之间的复合运算满足结合律的话,我们就可以把这种函数叫做 int 类型范畴上的“态射”,态射讲的是范畴内部元素间的映射关系,例如:

f,g,h 都是 int 类型范畴上的态射,因为函数的复合运算是满足结合律的。
我们还可以定义一种范畴间进行元素映射的函数,例如:
Func<int, double> ToDouble = x => Convert.ToDouble(x);这里的函数 Select 实现了 int 范畴到 double 范畴的一个映射,不过光映射元素是不够的,要是有一种方法能够帮我们把 int 中的态射(f,g,h),映射到 double 范畴中,那该多好。那么下面的函数 F 就帮助我们实现了这了功能。
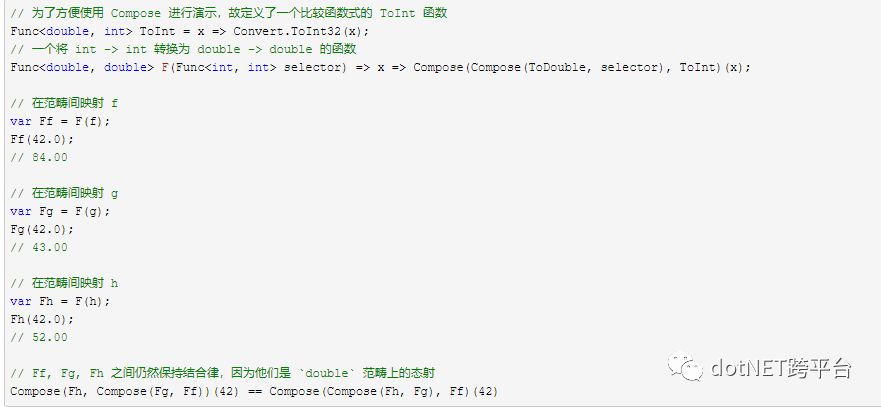
因为 F 能够将一个范畴内的态射映射为另一个范畴内的态射,ToDouble 可以将一个范畴内的元素映射为另一个范畴内的元素,所以,我们可以把 F与 ToDouble 的组合称作“函子”。函子体现了两个范畴间元素的抽象结构上的相似性。
相信看到这里你应该对范畴跟函子这两个概念有了一定的了解,现在让我们更进一步,看看 C# 中泛型与范畴之间的关系。
类型与范畴
在之前,我们是以数值为基础来理解范畴这个概念的,那么现在我们从类型的层面来理解范畴。
泛型是我们非常熟悉的 C# 语言特性了,泛型类型与普通类型不一样,泛型类型可以接受一个类型参数,看起来就像是类型的函数。我们把接受函数作为参数的函数称为高阶函数,依此类推,我们就把接受类型作为参数的类型叫做高阶类型吧。这样,我们就可以从这个层面把 C# 的类型分为两类:普通类型(非泛型)和高阶类型(泛型)。
前面的例子中,我列出的 f,g,h 能够完成 int -> int 的转换,因为它们是 int 范畴内的态射。而 ToDouble 能够完成 int -> double 的转换,那我们就可以将他看作是普通类型范畴的态射,类似的,我们还可以定义出 ToInt32,ToString 这样的函数,它们都能完成两个普通类型之间的转换,所以也都可以看作是普通类型范畴的态射。
那么对于高阶类型(也就是泛型)范畴来说,是不是也存在态射这样的东西呢?答案是肯定的,举个例子,用 LINQ 把 List<int> 转换成 List<double> :
Func<List<int>, List<double>> ToDoubleList = x => x.Select(ToDouble).ToList();不难发现,这里的 ToDoubleList 是 List<T> 类型范畴内的一个态射。不过你可能已经注意到了我们使用的 ToDouble 函数,它是普通类型范畴内的一个态射,我们仅仅通过一个 Select 函数就把普通类型范畴内的一个态射映射成了 List<T> 范畴内的一个态射(上面的例子中,是把 (int -> double) 转换成了 (List<int> -> List<double>)),而且 List<T> 还提供了能够把 int 类型转换成 List<int> 类型(type)的方法:new List<int>{ intValue },那么我们就可以把 List<T> 类(class)称为“函子”。事情变得有趣了起来。
自函子
List<T> 还有一个构造函数可以允许我们使用另一个 List 对象创建一个新的 List 对象:new List<T>(list),这完成了 List<T> -> List<T> 转换,这看起来像是把 List<T> 范畴中的元素重新映射到了 List<T> 范畴中。有了这个构造函数的帮助,我们就可以试着使用 Select 来映射 List<T>中的态射(比如,ToDoubleList):
// 这个映射后的 ToDoubleListAgain 仍然能够正常的工作Func<List<int>, List<List<double>>> ToDoubleListAgain = x => x.Select(e => ToDoubleList(new List<int>(){e})).ToList();这里的返回值类型看起来有些奇怪,我们得到了一个嵌套两层的 List,如果你熟悉 LINQ 的话,马上就会想到 SelectMany 函数——它能够把嵌套的 List 拍扁:
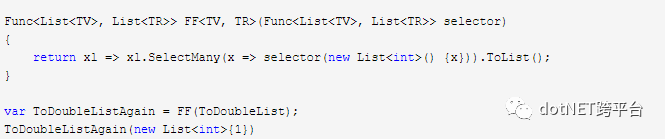
这样,我们就实现了 (List<T1> -> List<T2>) -> (List<T1> -> List<T2>) 的映射,虽然功能上并没有什么卵用,但是却实现了把 List<T> 范畴中的态射映射到了 List<T> 范畴中的功能。现在看来,List<T> 类不仅是普通类型映射到 List<T> 的一个函子,它也是 List<T> 映射到 List<T> 的一个函子。这种能够把一个范畴映射到该范畴本畴上的函子也被称为“自函子”。
我们可以发现,C# 中大部分的自函子都通过 LINQ 拓展方法实现了 SelectMany 函数,其签名是:
SomeType<TR> SelectMany<TV, TR>(SomeType<TV> source, Func<TV, SomeType<TR>> selector);List<T> 还有一个不接受任何参数的构造函数,它会创建出一个空的列表,我们可以把这个函数称作 unit,因为它的返回值在 List<T> 相关的一些二元运算中起到了单位 1 的作用。比如,concat(unit(), someList) 与 concat(someList, unit()) 得到的列表,在结构上是等价的。拥有这种性质的元素被称为“单位元”。
在函数式编程中,我们把拥有 SelectMany(也被叫做 bind),unit 函数的自函子称为“Monad”。
但是 C# 中并不是所有的泛型类是自函子,例如 Task<T>,如果我们不为它添加 Select 拓展方法,它连函子都算不上。所以如果把 C# 中全部的自函子类型放在一个集合中,然后把这些自函子类型之间用来做类型转换的全部函数(例如,list.ToArray() 等)看作是态射,那么我们就构建出来了一个 C# 中的“自函子范畴”。在这个范畴上,我们只能对 Monad 类型使用 LINQ 语法进行复合运算,例如上面的:
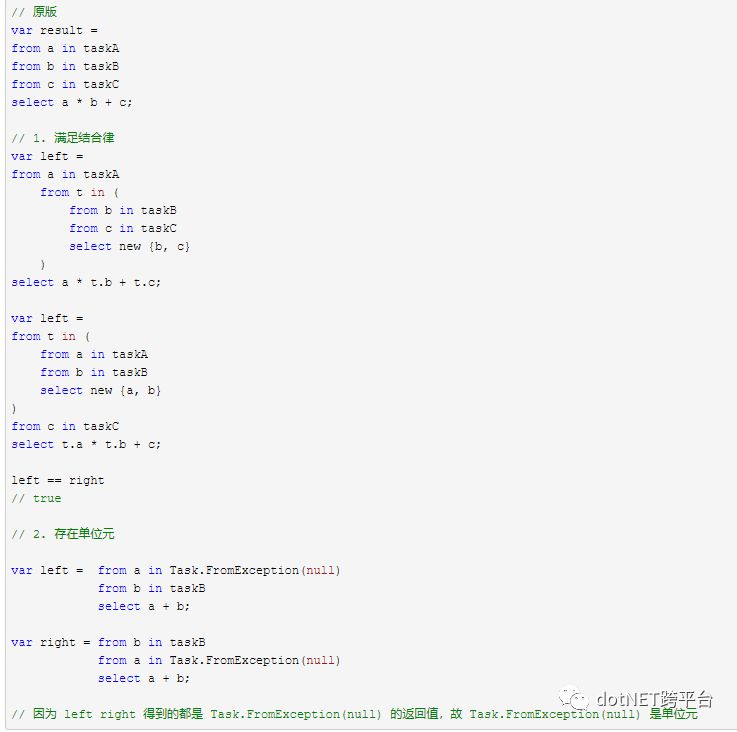
由于这种作用在两个 Monad 上面的二元运算满足交换律且 Monad 中存在单位元,与群论中幺半群的定义比较类似,所以,我们也把 Monad 称为“自函子范畴上的幺半群”。尽管这句话听起来十分的高大上,但是却并没有说明 Monad 的特征所在。就好比别人跟你介绍手机运营商,说这是一个提供短信、电话业务的公司,你肯定不知道他到底再说哪一家,不过他要是说,这是一个提供 5 元 30 M 流量包的手机运营商,那你就知道了他指的是中国移动。
个人体会
其实我一开始想写的内容只有 LINQ to Result 跟 LINQ to Task 的,但是在编写代码的过程中,种种迹象都表明着 LINQ 跟函数式编程中的 Monad 有不少关系,所以就把剩下的函数式编程这一部分给写出来了。
Monad 作为函数式编程中一种重要的数据类型,可以用来表达计算中的每一小步的功能,通过 Monad 之间的复合运算,我们可以灵活的将这些小的功能片段以一种统一的方式重组、复用,除此之外,我们还可以针对特定的需求(异步、错误处理、懒惰计算)定义专门的 Monad 类型,帮助我们以一种统一的形式将这些特别的功能嵌入到代码之中。在传统的面向对象的编程语言中 Monad 这个概念确实是不太好表达的,不过有了 LINQ 的帮助,我们可以比较优雅地将各种 Monad 组合起来。
用 LINQ 来对 Monad 进行运算的缺点,主要就是除了 SelectMany 之外的,我们没办法定义其他的能在 Query 语法中使用的函数了,要解决这个问题,请关注我的下一篇文章:“F# 函数式编程:Computational Expression”(挖坑预备)。
参考资料
https://zh.wikipedia.org/zh-hans/函子
https://en.wikipedia.org/wiki/Monad_(functional_programming)
http://hongjiang.info/understand-monad-4-what-is-functor/
原文地址: https://www.cnblogs.com/JacZhu/p/9729587.html
.NET社区新闻,深度好文,欢迎访问公众号文章汇总 http://www.csharpkit.com

)
)
![P4001-[ICPC-Beijing 2006]狼抓兔子【对偶图】](http://pic.xiahunao.cn/P4001-[ICPC-Beijing 2006]狼抓兔子【对偶图】)

 Round 1)
)

)


)


)
![P6640-[BJOI2020]封印【SAM,二分】](http://pic.xiahunao.cn/P6640-[BJOI2020]封印【SAM,二分】)

)

)
