正题
jozj 3447
题目大意
给你一个n*m的矩阵，每个位置有一个数，每一行每一列都只能选两个数，问你所选数字之和最大是多少
解题思路
对于该矩阵，我们可以建立一个网络图（如下图）
对于每一行建立建立一个点（下图第一列），连向S，费用为0，流量为2
对于每一列建立一个点（下图第二列），连向T，费用为0，流量为2
对于每个点连接相应的行和列，费用为该点的数字大小，流量为1
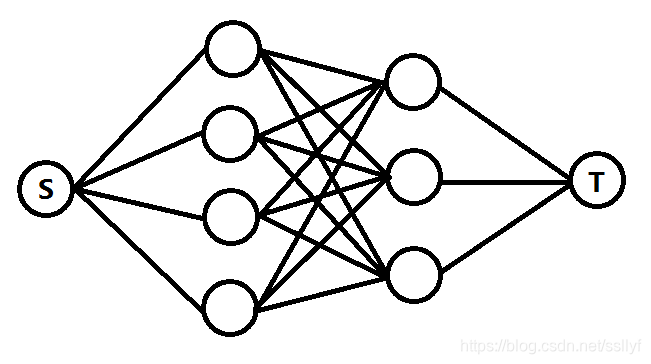
建好网络图后，跑最大费用即可（注意这里不能直接跑费用流，流量不一定最大）
该题求最大费用，如果跑反边，那么反边的边权绝对值会比上一条边大，因为会先跑费用大的，所以不存在负权回路，可以用SPFA
代码
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define N 10000
using namespace std;
const int inf = 1000000000;
int n, m, x, w, s, t, tot, ans, v[N], vv[N], p[N], b[N], ls[N], nx[N], head[N];
queue<int>d;
struct rec
{int to, next, lst, val;
}a[N];
void add(int x, int y, int z, int v)
{a[++tot].to = y;a[tot].lst = z;a[tot].val = -v;a[tot].next = head[x];head[x] = tot;a[++tot].to = x;a[tot].lst = 0;a[tot].val = v;a[tot].next = head[y];head[y] = tot;return;
}
bool spfa()
{memset(b, 127 / 3, sizeof(b));memset(p, 0, sizeof(p));memset(ls, 0, sizeof(ls));memset(nx, 0, sizeof(nx));while(!d.empty()) d.pop();p[s] = 1;b[s] = 0;ls[s] = inf;d.push(s);while(!d.empty()){int h = d.front();d.pop();for (int i = head[h]; i; i = a[i].next)if (b[h] + a[i].val < b[a[i].to] && a[i].lst){b[a[i].to] = b[h] + a[i].val;ls[a[i].to] = min(ls[h], a[i].lst);nx[a[i].to] = i;if (!p[a[i].to]){p[a[i].to] = 1;d.push(a[i].to);}}p[h] = 0;}return ls[t] > 0 && b[t] < 0;//保证费用大于0（这里建立负边跑最短路）
}
void dfs()
{int now = t;while(nx[now]){a[nx[now]].lst -= ls[t];a[nx[now]^1].lst += ls[t];now = a[nx[now]^1].to;}ans += b[t] * ls[t];return;
}
int main()
{scanf("%d%d", &n, &m);tot = 1;s = ++w;t = ++w;for (int i = 1; i <= n; ++i)//建图{v[i] = ++w;add(s, v[i], 2, 0);}for (int i = 1; i <= m; ++i){vv[i] = ++w;add(vv[i], t, 2, 0);}for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j){scanf("%d", &x);if (!x) continue;add(v[i], vv[j], 1, x);}while(spfa())dfs();printf("%d", -ans);return 0;
}
