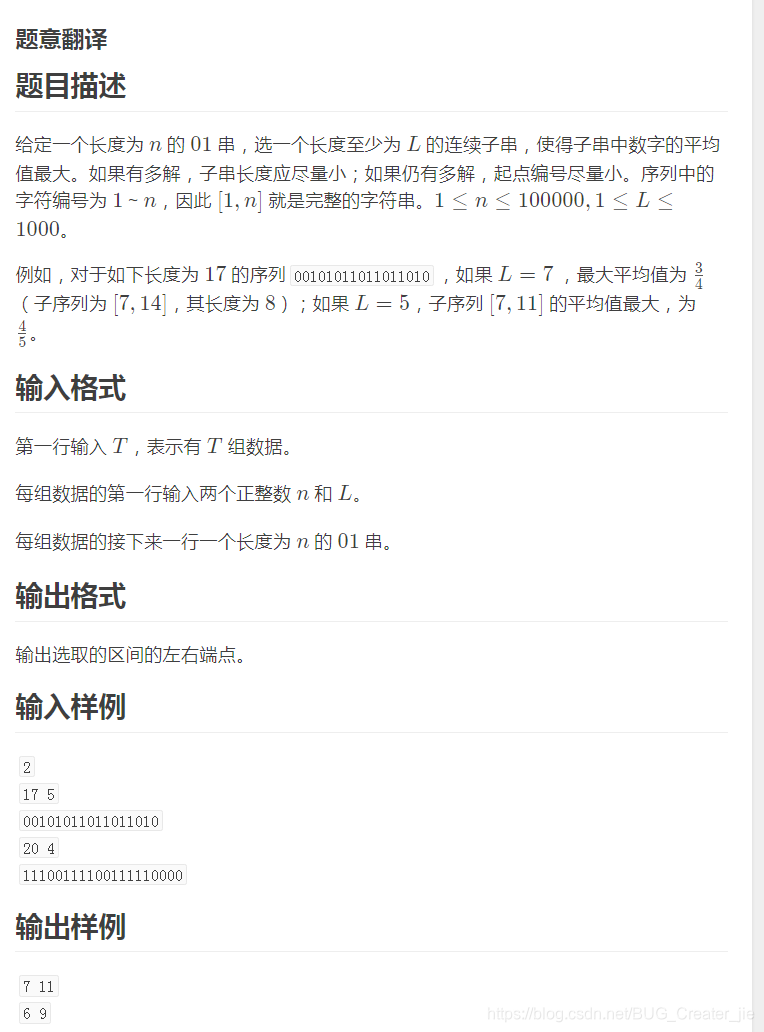
解析
这道题寻找平均值的max,答案明显具有单调性,所以采用二分算法
从0到1不断取中点mid作为平均值的可能点,看是否存在不短于l的数列均值>=mid不难得到以下代码:
double st=0,ed=1;for(int i=1;i<=10;i++){double mid=(st+ed)/2;if(check(mid)) st=mid;else ed=mid;}
现在的问题就是要解决这个check函数的写法了
因为N范围到1e5,暴力的On方肯定是会超的
我们想到可以先把数组都减mid,这样就转化为是否存在不短于L的数列加和大于等于0的问题
我们用s[i]表示1到i的加和
那么a到b的和可以转化为s[b] - s[a-1](其中b-a+1 >=l)
要使s[b] - s[a-1]最大,就要使s[a-1]取的是s[0]到s[b-l+1]的最大值
而随着b从l循环到n,每次s[a-1]只加入了一个可能取的元素,故只需与该新值取min,不必遍历
代码如下:
double mn=M;for(int i=l;i<=n;i++){mn=min(mn,s[i-l]);if(s[i]-mn>=0) return true;//只要存在就返回true }return false;
这样check函数的时间复杂度就为O(n)
AC快乐~~~~~~
代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int M = 2e9;
int n,l,t;
int zuo,you;
int f[100500];
bool check(double x){double s[100500]={ };s[1]=f[1] - x;for(int i=2;i<=n;i++){s[i] = s[i-1] + f[i] -x;//求减完x的前缀和 }double mn=M;for(int i=l;i<=n;i++){mn=min(mn,s[i-l]);if(s[i]-mn>=0) return true;//只要存在就返回true }return false;
}
int main(){scanf("%d",&t);for(int k=1;k<=t;k++){scanf("%d%d",&n,&l);for(int i=1;i<=n;i++){scanf("%1d",&f[i]);}double st=0,ed=1;for(int i=1;i<=10;i++){double mid=(st+ed)/2;if(check(mid)) st=mid;else ed=mid;}double x=st;double s[100500]={ };s[1]=f[1] - x;for(int i=2;i<=n;i++){s[i] = s[i-1] + f[i] -x;}int a,flag=0;double mn=M;for(int i=l;i<=n;i++){if(mn>s[i-l]){mn=s[i-l];a=i-l;}if(s[i]-mn>=0){if(flag==0){zuo=a+1;you=i;flag=1;}else if(you-zuo>i-a){zuo=a+1;you=i;}}}printf("%d %d\n",zuo,you);}return 0;
}


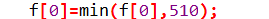


![二分:[BJWC2008]秦腾与教学评估](https://img-blog.csdnimg.cn/20210126180055799.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0JVR19DcmVhdGVyX2ppZQ==,size_16,color_FFFFFF,t_70)




![hash:奶牛看地图(洛谷P3405 [USACO16DEC]Cities and States S)](https://img-blog.csdnimg.cn/20210128211531142.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0JVR19DcmVhdGVyX2ppZQ==,size_16,color_FFFFFF,t_70)

