容器是应用走向云端之后必然的发展趋势，因此笔者非常乐于和大家分享我们这段时间对容器的理解、心得和实践。

本篇教程持续编写了2个星期左右，只是为了大家更好地了解、理解和消化这个技术，能够搭上这波车。

你可以关注我们的公众号“magiccodes”给我们留言，也可以加入我们的QQ群（85318032）一起讨论，我们希望能够多多交流，多多分享。

如果觉得不错，请多多点赞或者请我们喝杯咖啡，你们的支持是我们前进的最大动力！

目

录

目

录

前言

随着生产力的发展尤其是弹性架构的广泛应用（比如微服务），许多一流开发者都将应用托管到了应用容器上，比如Google、微软、亚马逊、腾讯、阿里、京东和新浪。

从未来的发展方向来看，容器引擎将会越来越成为主流，哪怕不是弹性架构，托管到应用容器也将是一种趋势——因为更低的开发运维和托管成本以及对服务器的资源的优化配置。而且未来一个很大的趋势是——无服务器计算服务。

因为相对于软件、硬件在本地设备中的分裂，云计算的一大特性就是将服务构建在云上，供多种设备同时无缝调用。但事实上，云服务在发展的过程中还没能实现共融共通的理想——比如，各家的云服务是相对割裂的，开发者基于Google云服务构建的软件拿到亚马逊的AWS上也许就不能用了，阿里云的应用迁移到腾讯云可能就存在问题了；在任务执行层面，为防止互相干扰，云服务厂商在同一台服务器上执行多个任务时也会将它们隔离进行。很明显，这样的实际情况和云服务的初始理念相去甚远。而利用容器技术，软件可以快速在各类云服务和基础设施上转换。而且，当割裂问题被解决之后，软件也有望在瞬间获取大量的计算能力。

而Docker，就是容器引擎中的佼佼者，并且已经得到了广泛的实践和应用。有了Docker之后，软件的开发工作将会变得更加容易。比如，开发者们在笔记本电脑上写完一个软件后，可以将它转移到云服务上运行而无需做出更改；无论是自己的服务器、数据中心还是Google、微软、阿里云的云计算服务器，开发人员都可以按自己的想法在任何基础设施之间转移自己的软件。这也是未来的一个愿景——机器和基础设施是可以互相替代的，整个互联网就是一个巨大的计算机。

Docker是如此令人向往和引人深入，但是在国内，开发者普遍迁移到云端基本上也都是只用到了虚拟机等基础设施，其实大家都听说过Docker，但是总是有一道门槛挡在大家面前导致大家无法逾越或者产生了一些偏见：

• 缺乏完整的系统的教程和实践，开发者普遍认为使用Docker很麻烦，只有大公司能用，门槛很高；

• 云端容器服务产品用户体验不够，对于初学者门槛太高——这个太高指的是消化这些概念和理念，并且能够掌握和可控；

• 对容器服务的认知还不够，对它的好处以及吸引之处还不太了解；

• 认为对现有系统、架构改造太大，成本太高；

• 认为Docker只是一种单纯的相对先进的技术，并不能给现有的开发带来什么改变；

什么是Docker

Docker 是一个开源的应用容器引擎，可以轻松的为任何应用创建一个轻量级的、可移植的、自给自足的容器。开发者在本地编译测试通过的容器可以批量地在生产环境中部署，包括VMs（虚拟机）、bare metal、OpenStack 集群和其他的基础应用平台。

简单的理解，Docker类似于集装箱，各式各样的货物，经过集装箱的标准化进行托管，而集装箱和集装箱之间没有影响。也就是说，Docker平台就是一个软件集装箱化平台，这就意味着我们自己可以构建应用程序，将其依赖关系一起打包到一个容器中，然后这容器就很容易运送到其他的机器上进行运行，而且非常易于装载、复制、移除，非常适合软件弹性架构。

因此，就像船只、火车或卡车运输集装箱而不论其内部的货物一样，软件容器充当软件部署的标准单元，其中可以包含不同的代码和依赖项。 按照这种方式容器化软件，开发人员和 IT 专业人员只需进行极少修改或不修改，即可将其部署到不同的环境。

总而言之，Docker 是一个开放平台，使开发人员和管理员可以在称为容器的松散隔离的环境中构建镜像、交付和运行分布式应用程序。以便在开发、QA 和生产环境之间进行高效的应用程序生命周期管理。

Docker和虚拟机的区别

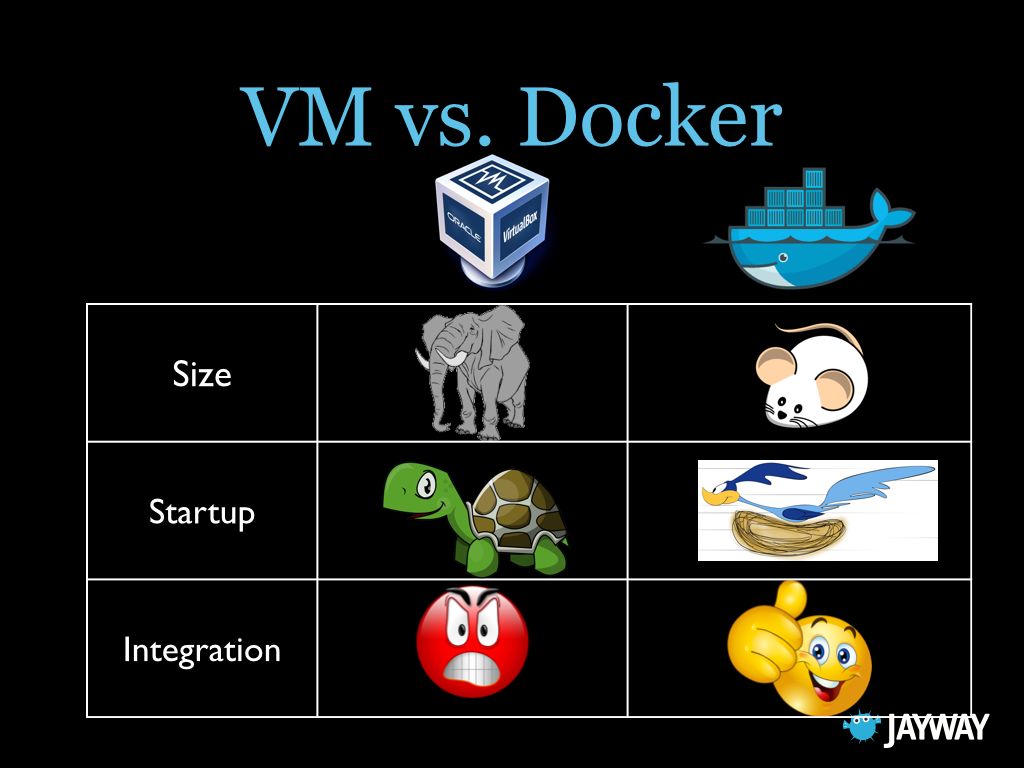
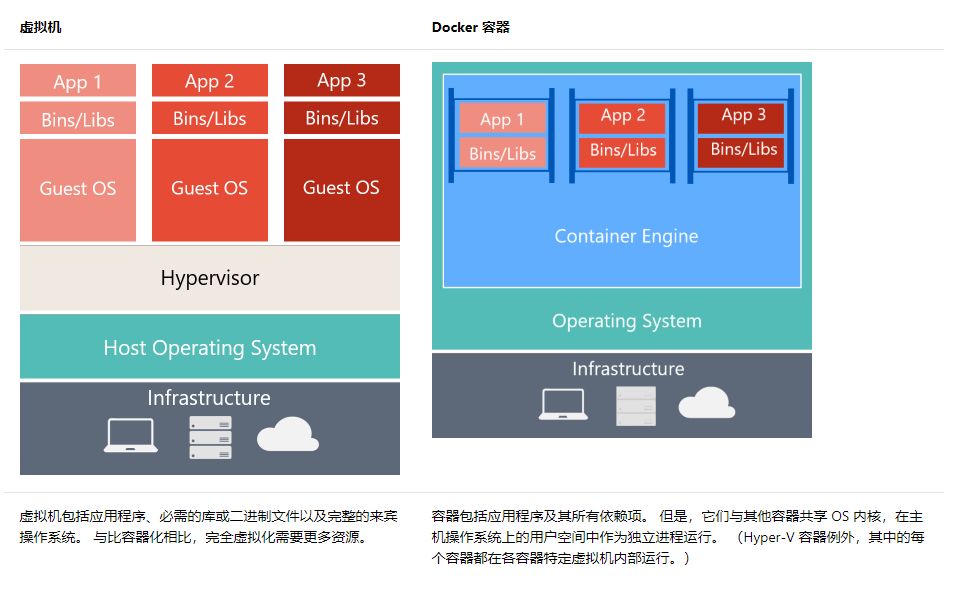
如上图所示，由于容器所需的资源要少得多（例如，它们不需要一个完整的 OS），所以它们易于部署且可快速启动。这使你能够具有更高的密度，也就是说，这允许你在同一硬件单元上运行更多服务，从而降低了成本。

在同一内核上运行的副作用是，你获得的隔离比 VM 要少。

镜像的主要目标是使环境（依赖项）在不同的部署中保持不变。 也就是说，可以在计算机上调试它，然后将其部署到保证具有相同环境的另一台计算机上。

借助容器镜像，可打包应用或服务并采用可靠且可重现的方式对其进行部署。可以说 Docker 不只是一种技术，还是一种原理和过程。

在使用Docker之前，我们经常会听到，“这个问题在开发环境是正常的！”。而在使用 Docker 后，你不会听到开发人员说：“为什么它能在我的计算机上使用却不能用在生产中？”。开发人员只需说“它在 Docker 上运行”，因为打包的 Docker 应用程序可在任何支持的 Docker 环境上执行，而且它在所有部署目标（例如，开发、QA、暂存和生产）上都按预期运行。

基本概念

镜像：一个特殊的文件系统

操作系统分为内核和用户空间。对于 Linux 而言，内核启动后，会挂载 root 文件系统为其提供用户空间支持。而 Docker 镜像（Image），就相当于是一个 root 文件系统。

Docker 镜像是一个特殊的文件系统，除了提供容器运行时所需的程序、库、资源、配置等文件外，还包含了一些为运行时准备的一些配置参数（如匿名卷、环境变量、用户等）。

镜像不包含任何动态数据，其内容在构建之后也不会被改变。

Docker 设计时，就充分利用 Union FS 的技术，将其设计为分层存储的架构。 镜像实际是由多层文件系统联合组成。

镜像构建时，会一层层构建，前一层是后一层的基础。每一层构建完就不会再发生改变，后一层上的任何改变只发生在自己这一层。

比如，删除前一层文件的操作，实际不是真的删除前一层的文件，而是仅在当前层标记为该文件已删除。

在最终容器运行的时候，虽然不会看到这个文件，但是实际上该文件会一直跟随镜像。

因此，在构建镜像的时候，需要额外小心，每一层尽量只包含该层需要添加的东西，任何额外的东西应该在该层构建结束前清理掉。

分层存储的特征还使得镜像的复用、定制变的更为容易。甚至可以用之前构建好的镜像作为基础层，然后进一步添加新的层，以定制自己所需的内容，构建新的镜像。

容器：镜像运行时的实体

镜像（Image）和容器（Container）的关系，就像是面向对象程序设计中的类和实例一样，镜像是静态的定义，容器是镜像运行时的实体。容器可以被创建、启动、停止、删除、暂停等 。

容器的实质是进程，但与直接在宿主执行的进程不同，容器进程运行于属于自己的独立的命名空间。前面讲过镜像使用的是分层存储，容器也是如此。

容器存储层的生存周期和容器一样，容器消亡时，容器存储层也随之消亡。因此，任何保存于容器存储层的信息都会随容器删除而丢失。

按照 Docker 最佳实践的要求，容器不应该向其存储层内写入任何数据 ，容器存储层要保持无状态化。

所有的文件写入操作，都应该使用数据卷（Volume）、或者绑定宿主目录，在这些位置的读写会跳过容器存储层，直接对宿主（或网络存储）发生读写，其性能和稳定性更高。

数据卷的生存周期独立于容器，容器消亡，数据卷不会消亡。因此， 使用数据卷后，容器可以随意删除、重新 run，数据却不会丢失。

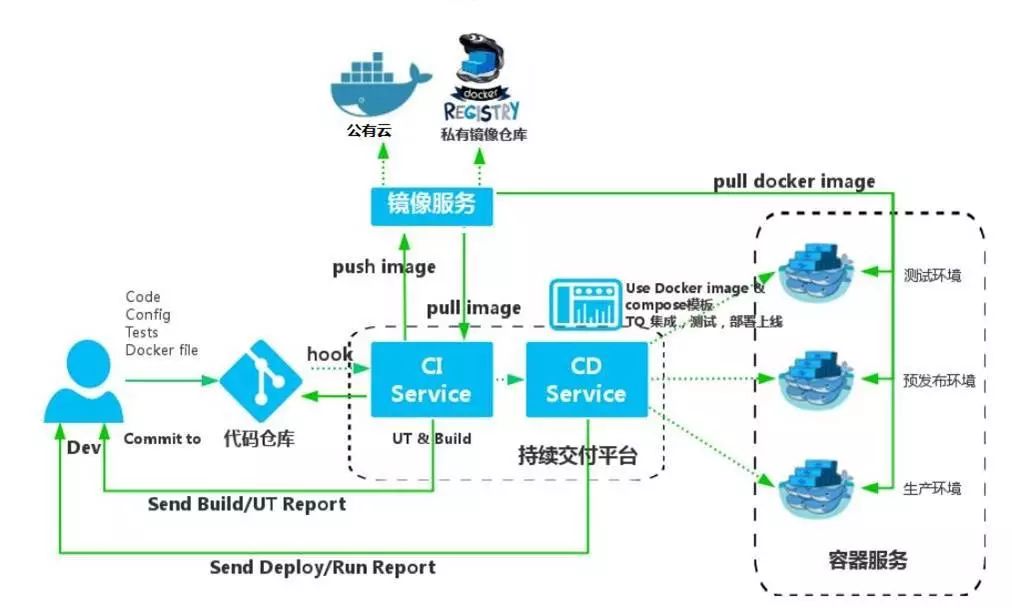
注意：

容器在整个应用程序生命周期工作流中提供以下优点：隔离性、可移植性、灵活性、可伸缩性和可控性。 最重要的优点是可在开发和运营之间提供隔离。

仓库：集中存放镜像文件的地方

镜像构建完成后，可以很容易的在当前宿主上运行，但是， 如果需要在其他服务器上使用这个镜像，我们就需要一个集中的存储、分发镜像的服务，Docker Registry 就是这样的服务。

一个 Docker Registry 中可以包含多个仓库（Repository）；每个仓库可以包含多个标签（Tag）；每个标签对应一个镜像。

所以说，镜像仓库是 Docker 用来集中存放镜像文件的地方，类似于我们之前常用的代码仓库。

通常，一个仓库会包含同一个软件不同版本的镜像，而标签就常用于对应该软件的各个版本 。

我们可以通过<仓库名>:<标签>的格式来指定具体是这个软件哪个版本的镜像。如果不给出标签，将以 latest 作为默认标签。

这里补充一下 Docker Registry 公开服务和私有 Docker Registry 的概念：

Docker Registry 公开服务是开放给用户使用、允许用户管理镜像的 Registry 服务。

一般这类公开服务允许用户免费上传、下载公开的镜像，并可能提供收费服务供用户管理私有镜像。

最常使用的 Registry 公开服务是官方的 Docker Hub ，这也是默认的 Registry，并拥有大量的高质量的官方镜像，网址为：hub.docker.com/ 。

在国内访问 Docker Hub 可能会比较慢，国内也有一些云服务商提供类似于 Docker Hub 的公开服务。

除了使用公开服务外，用户还可以在本地搭建私有 Docker Registry 。Docker 官方提供了 Docker Registry 镜像，可以直接使用做为私有 Registry 服务。

开源的 Docker Registry 镜像只提供了 Docker Registry API 的服务端实现，足以支持 Docker 命令，不影响使用。但不包含图形界面，以及镜像维护、用户管理、访问控制等高级功能。

长按识别二维码，了解后续精彩内容

如果喜欢作者的文章，请关注“magiccodes”订阅号以便第一时间获得最新内容。本文版权归作者和湖南心莱信息科技有限公司共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。

QQ群：

编程交流群<85318032> 

产品交流群<897857351>