点击蓝字

关注我

碧点公司（Green Dot）是仔细聆听消费者心声，以消费者为导向的金融科技创新公司，致力于为大众带来高效、便捷与体验舒适的个人银行业务。Green Dot创造了预付借记卡产业，也是美国最大的可增值预付借记卡和现金充值业务服务供应商。

在2018年11月23日-24日举办的GreenDot Hackathon活动上，来自Web团队的四名开发人员 Edi Wang、Eric Wang、Emon Zan 和Jimmy Yang 组成的 “TBD” 小组，将微软智慧云Azure的人工智能服务与公司客服业务紧密结合，实现了人工智能赋能客服机器人的效果。该机器人能够理解人类自然语言，并在实时聊天中使用语音或文字准确回答用户提问，这将极大缓解人工客服的压力。

传统客服经常需要面对复杂的用户提问，而这些提问可以总结为几个常见问题，我们称之为FAQ。这不仅大量占用时间和精力，还可能造成人工座席持续繁忙，其他用户等待时间过长，甚至造成流失用户的严重后果。如果将这些FAQ交给聊天机器人去回答，只让人工处理机器人解答特定的复杂问题，能够大大提高人工客服的利用率与价值。

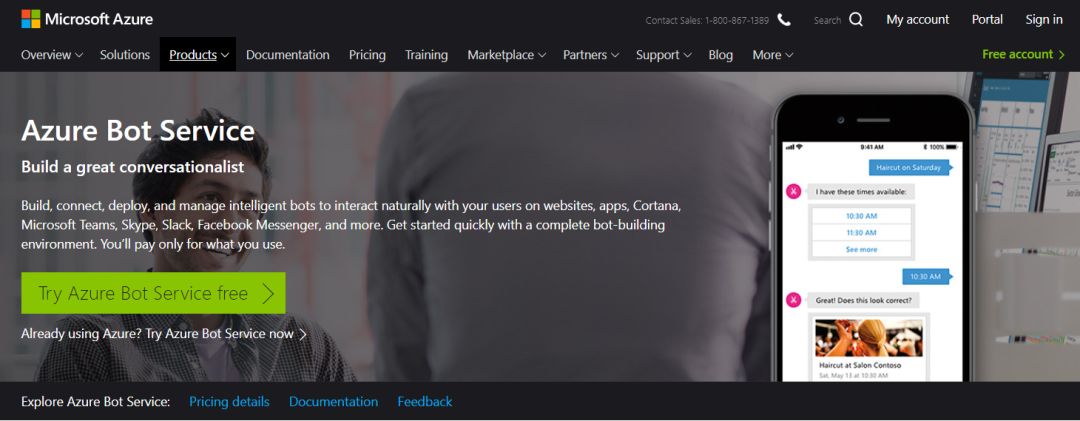
微软Azure的目标是让人工智能（Artificial Intelligence, AI）平民化，即让开发者在无需了解AI原理、算法和模型训练等复杂细节的前提下，就能够便捷的享用AI服务。Azure上的 “QnA Maker” 则对Bot Framework进行一站式包装，让开发者能够根据公司已有的FAQ数据，在短短几分钟内，生成一个完整可用的FAQ聊天机器人。整个过程中，我们没有自己选择及编写算法，也没有自己进行模型训练与API编写，更没有自建数据索引，甚至连工程代码都是Azure全自动完成，智能水平让人震惊到合不拢嘴！

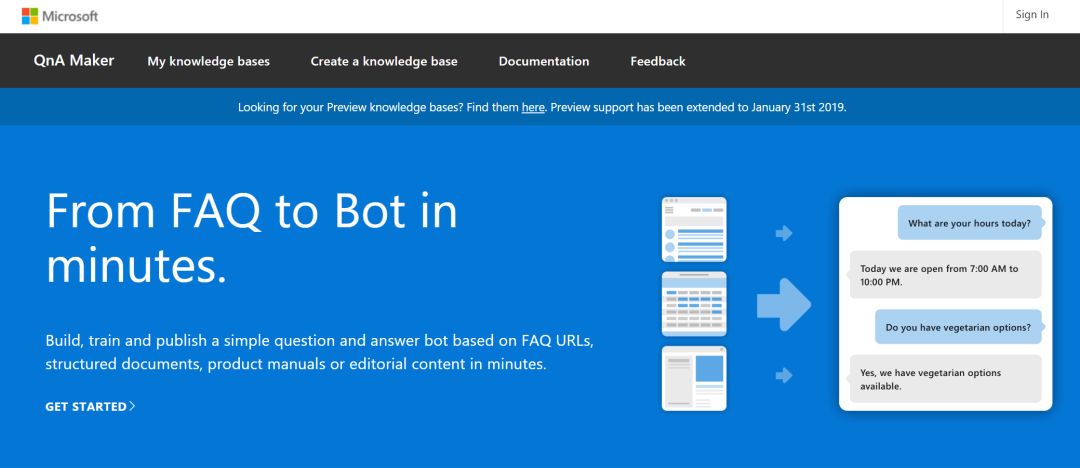
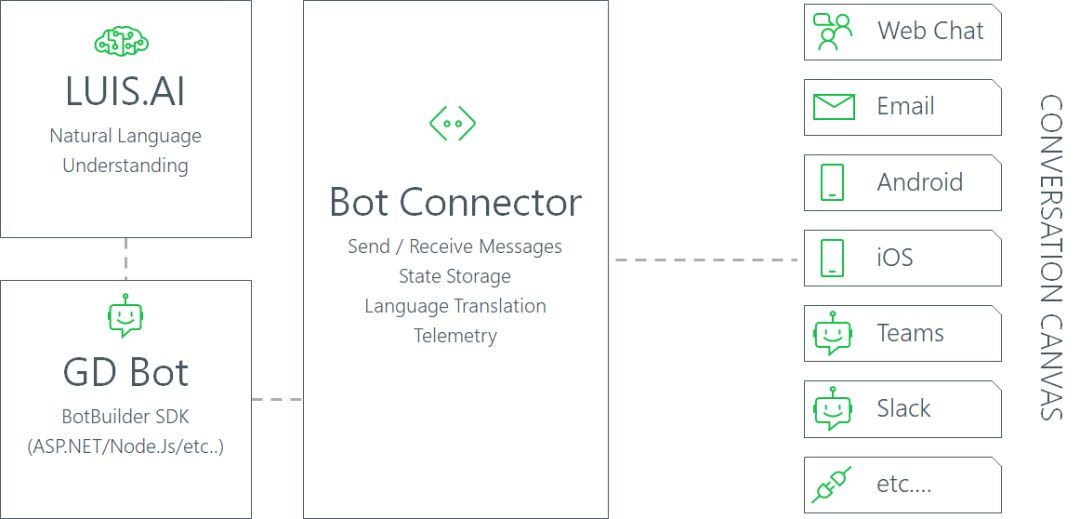
QnA机器人可以通过Bot Connector直接整合到Green Dot的现有产品中，如官网页面、手机App以及Teams、Slack等聊天工具。如今，在萨提亚·纳德拉先生带领下，微软开源开放，不再局限于自家技术，而是海纳百川、开放胸怀迎接各类先进技术接入，因此我们可以用任何语言、任何平台完成云服务的整合。

TBD小组成员Emon Zan使用微软的ASP.NET Core 2.1及谷歌的Angular 6在短短几小时内，完成了机器人到公司官网的整合。结合Green Dot配色与icon，达到了用户体验的高度一致。值得一提的是，通过整合微软的语音API，该机器人能够方便地实现语音输入及语音回复。

Emon之前没有接触过Azure，也并不了解认知服务，而她在短短几个小时内就能完成AI服务的整合，足以证明该平台的易用性。微软将极端复杂的人工智能变得触手可及，就像几十年前微软将复杂的计算机变得人人都能用那样。

Azure Bot Service提供了极易整合的JavaScript库，几行代码就能直接嵌入聊天窗口。同时也照顾到要求高度自定义的用户，提供了REST API，以便企业灵活实现客户端界面。

诚然，机器人并不能解答所有用户提问，人工客服必不可少。但是如果让用户与人工客服另起一次对话，用户需要再次向客服人员阐述问题背景，显然非常重复与麻烦。TBD小组基于微软QnA机器人的代码及模拟器，进行二次开发，整合了SignalR实时Web通讯框架，一旦机器人遇到无法回答的问题，客服人员可以直接在后台看到用户之前与机器人的全部会话，并直接在后台回复，这个过程对用户来说非常透明，在不需要切换页面的情况下，直接在当前窗口与客服人员对话。

机器人的代码更新也十分方便，微软Azure中的DevOps服务可以一键配置生产环境到代码托管服务的整个编译、测试、发布流程。线上的机器人后台也能够通过Application Insight以实时图表的方式来监控运行情况，让运维人员对引用健康了如指掌。

另外，微软的认知服务（Cognitive Services）是世界上唯一一款可以通过容器技术部署到本地数据中心运行的人工智能服务，即使在没有到公有云连接的边缘环境也能拥有一定的AI能力，对于Green Dot这样注重信息安全的银行来说，显得尤为重要。

微软智慧云Azure帮助Green Dot在极短时间内实现了一个可用的解决方案，在这个竞争激烈的世界里，快速推向市场是企业成功的关键。作为微软MVP，很高兴能帮助企业使用微软技术获得成功，一起见证 “予力全球每一人，每一组织，成就不凡” 的使命！

了解更多Azure Bot Service特性，请戳链接：https://azure.microsoft.com/en-us/services/bot-service

(部分图片来源于网络)