前言

什么是分布式系统?关于这点其实并没有明确且统一的定义。在我看来,只要一个系统满足以下几点就可以称之为分布式系统

• 系统由物理上不同分布的多个机器节点组成

• 系统的多个节点通过网络进行通信,协调彼此之间的工作。

• 系统作为整体统一对外提供服务,其分布式细节对客户端透明。

要想更好的理解分布式系统,并正确使用甚至构建分布式系统,需要理解其中的两个关键概念——分布式系统的数据一致性和分布式系统的幂等性。

1. 分布式系统的数据一致性

对于分布式系统,数据可能存在于不同的物理节点上,节点之间只能通过网络进行通信来协调彼此之间的状态,而网络通信需要时间并且其本身并不十分可靠,因而如何保持数据一致性成为了分布式系统的难题。对于不同的分布式系统,其一致性语义以及面对的一致性难题可能略有差别

1.1 分布式存储系统中的一致性问题

在分布式存储系统中,为了保持系统的高可用,同时增加读操作的并发性,同一份数据会有多份副本,不同的副本存储于不同的节点上,如下图所示

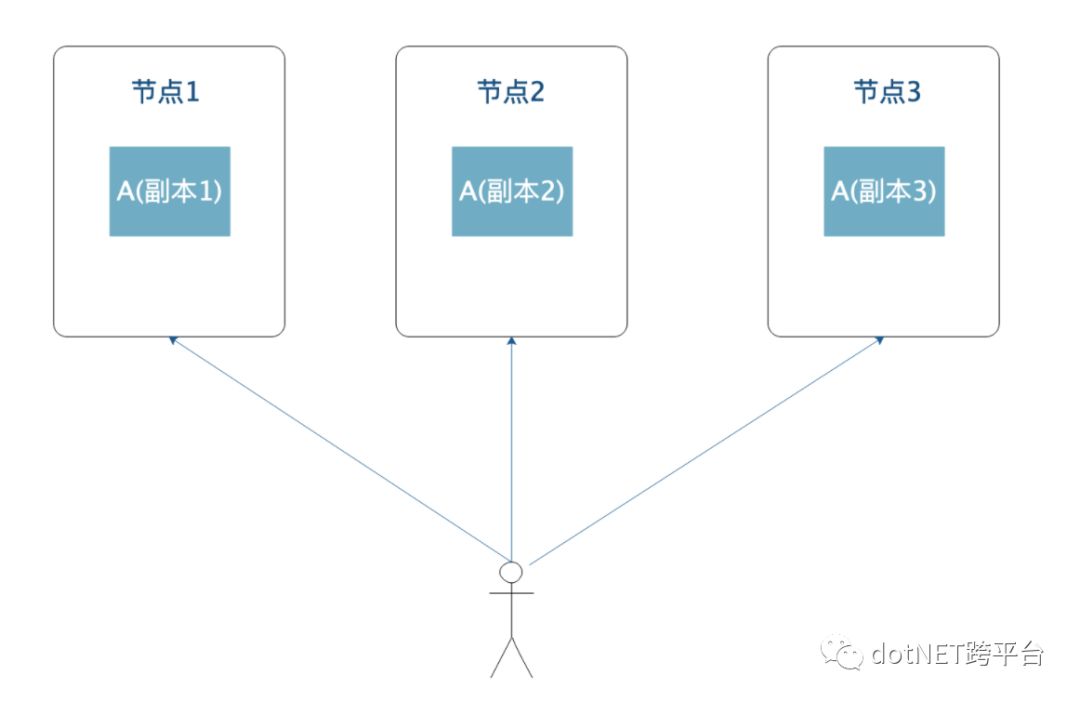
在并发环境下,因为存在多个客户端同时读取同一数据在不同节点上的副本,因而如何维护数据的一致性视图就非常重要,即对于使用该分布式系统的客户端而言,对于多副本数据的读写其表现应该和单份数据一样,通常系统是通过数据复制的方式来达到这一点的,

• 客户端将节点1中的副本A修改为10,系统将通过网络通信的方式将节点2和节点3中的副本A也更新为10。然而网络通信是需要时间的,假设在系统还未将节点1中的A值同步到节点2和节点3,此时另一个客户端访问了节点2和节点3,这个时候系统怎么办？

• 甚至,考虑更极端的场景,节点之间的网络被断开,不同节点无法感知到彼此的存在,当然也就无法保持多副本数据的同一视图,那么这个时候系统又该怎么办？

1.2 微服务应用的分布式一致性问题

微服务架构下,原有的单体应用按功能被拆分成一个个微服务应用,每个微服务应用被部署在不同的机器节点上,只完成原有单体应用的某一部分功能,操作属于该业务功能的数据库或表。彼此之前通过网络通信的方式协调彼此之间的工作,作为整体共同对外提供服务,因而一个业务功能的实现,可能会涉及到多个微服务的调用,操作物理上不同的多个数据库或表。比如对于下单并支付这个业务功能而言,需要调用下单微服务和支付微服务来共同完成。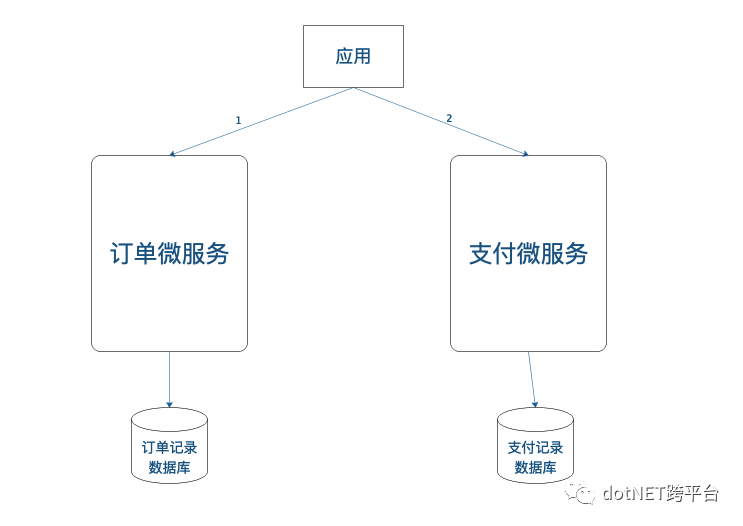

对于下单并支付这一业务功能,应用先调用订单微服务,在订单数据库中添加一条订单记录,成功后再调用支付微服务添加相应的支付记录,只有这两个微服务都调用成功,该业务功能才算执行成功。这个过程可能存在以下的问题:

• 订单微服务调用成功,订单记录已落地,但是支付微服务由于各种原因迟迟得不到响应,此时用户通过订单号查询只能查到订单记录而查不到支付记录,这对于已经成功付款的用户而言肯定是无法接受的,这种情况该怎么办？

• 订单微服务调用成功,订单记录已落地,但是支付微服务调用失败,此时订单记录和支付记录所对应的业务状态不一致,这时候系统该怎么办?

1.3 对于一致性的正确理解

分布式存储系统的一致性问题,主要在于如何维持多副本的一致性视图上,即如何使多份数据对外表现的和一份数据一样。而微服务架构下的分布式应用系统,其一致性问题主要在于如何使不同微服务的数据对同一业务状态的描述保持一致,比如对于下单并支付这一业务操作而言,下单和支付要么同时成功,要么应该同时失败,而不应该一个成功一个失败,并且在这个过程中,某部分已经成功或失败的数据是否应该对客户端可见。在联系一下本地事务ACID中的一致性,我们可能会产生一定的混乱:它们讲的一致性是一个东西吗？先说下我的个人理解:不管是ACID的一致性还是不同分布式系统中的一致性,它们本质上讲的是一件事:数据的一致性,在于正确的反应现实世界,对发生于现实世界的事情的正确描述。这就要求,一致性的数据至少要满足以下两个条件:

• 1.符合系统本身具有的约束条件,比如数据库中的数据要遵循主码,外码,check约束。

• 2.与特定业务有关的所有数据,它们对业务执行状态的描述应该保持一致。比如从A账户转账100元到B账户这一业务操作,不管A账户和B账户是否在一个数据库,也不管这一业务操作是否执行成功,两个账户的总金额应该保持不变;如果有关账户金额的数据存储在分布式系统的多个不同的副本,则这些副本的数据应该一样。

从这个意义上,不管是单机数据库还是分布式存储系统还是微服务架构下的分布式应用,对一致性的追求本质上是一样的:在满足系统本身约束的前提下,对于发生的业务操作及其执行状态的一致性描述。只不过由于分布式系统数据的分布式存储以及网络通信状况的复杂,使得分布式系统要保持数据一致性相比单机应用要考虑更多复杂的因素,实现也要困难的多。很多文章把它们做了严格的区分,个人觉得很没有必要,也不利于对于一致性的正确理解,从哲学的角度看,是割裂了事物共性和个性之间的联系。

2.分布式一致性模型

就好像单机数据库中为事务的隔离性设置了不同的级别,分布式系统中对数据的一致性级别也有分类。总的来说可以分为强一致性和弱一致性两大类,弱一致性中又可以继续细分为最终一致性,因果一致性,会话一致性,单调读一致性和单调写一致性等多种,不过弱一致性中只有最终一致性比较重要,其他的可以暂时忽略。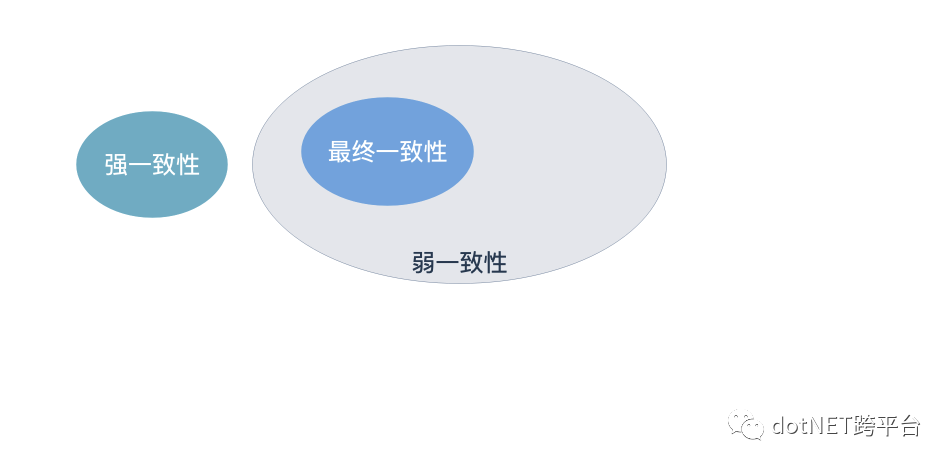

• 强一致性
  以带多副本的分布式存储系统为例,所有连接到分布式系统的客户端看到的某一数据的值都是一样的。当某个客户端修改了这个值,后续的所有客户端都能读取到这个更新的值,并且所有的更新操作都在这个新的值的基础上进行,直到这个值被再次修改,如下图所示,在A修改X前所有客户端都能读取到X的值为1,在A将X修改为2之后,所有客户端都能读取到这个更新后的值。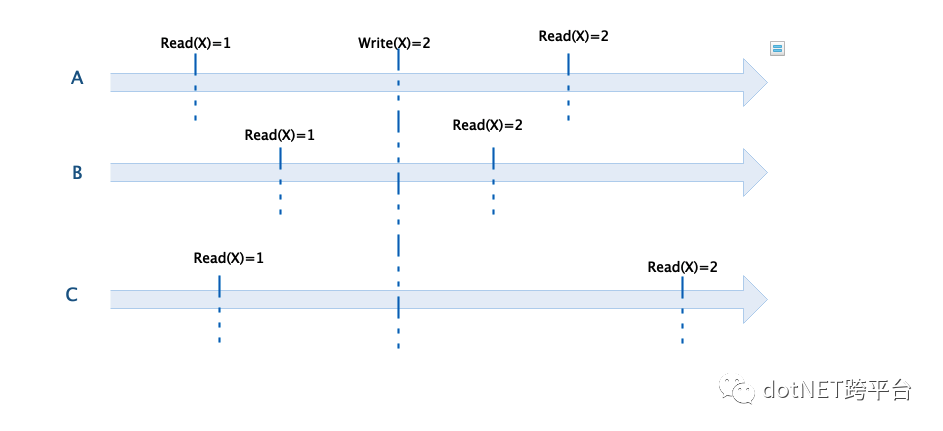
  

• 最终一致性
  所有不能满足强一致性要求的都称为弱一致性,而最终一致性是其中比较强的一种。在最终一致性模型下,当数据项X被修改后,客户端并不一定能马上看到这个更新后的值(有些可能读取到了新值,有些读取到的可能还是旧值),但是在一段时间后,所有客户端都能读取到这个更新后的值并进行相关操作。最终一致性模型下,分布式数据最终能达到一致,但是需要经过一段时间,这段时间称为不一致窗口。
  如下图所示,在A将X修改为2后,在不一致窗口内只有B能读取到X=2,其他客户端读取到的依旧是X=1。但是在不一致窗口后,所有客户端都能读取到X=2。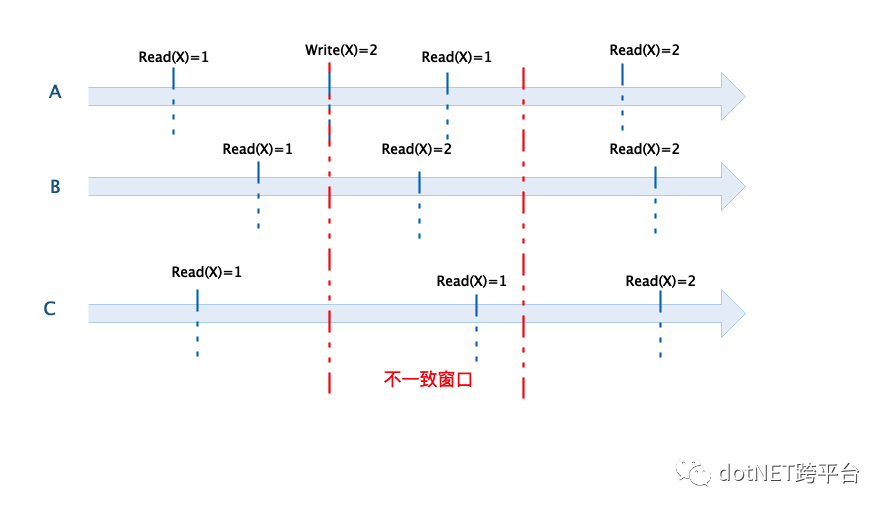
  

3. 追求强一致性的约束——CAP定理

严格意义上来讲,真正的一致性模型只有一种——强一致性,这也是一种理想化的模型。它为分布式数据维护了完全一致的视图,使得一旦修改了数据后,所有客户端能够马上看到这个更新后的值并基于这个新值进行后续的操作,使得我们操作分布式数据和操作本地数据一样。在分布式系统中要实现一致性需要考虑其他因素,比如可用性和分区容忍性,而这些因素相互有制约,这种制约关系在CAP定理中被很好的进行了描述。

CAP是"Consistency","Availabilty","Partition Tolerance"的简称,分别代表了:强一致性,可用性和分区容忍性,它们的含义分别如下:

• 强一致性:在分布式系统同一份数据有多副本的情况下,对于数据的操作效果和只有单份数据一样。

• 可用性:客户端在任何时刻对数据的读/写操作都应该保证在时限内完成。

• 分区容忍性:当分布式系统出现网络分区,不同分区间的机器无法进行网络通信时,系统仍然能够继续工作。

CAP定理的内容:对于一个分布式系统,无法同时实现强一致性,可用性和分区容忍性,即CAP三要素不可兼得。

3.1 如何理解CAP三要素不可兼得

由于网络的不可靠性,网络分区的情况不可避免的会发生,当出现网络分区时,不同分区的机器无法进行通信。分布式系统必须能够在出现网络分区的情况下继续工作,因而对于分布式系统而言,P即分区容忍性是必须要具备的要素,那么问题就转化为了,在系统满足分区容忍性的前提下,为什么强一致性和可用性不可兼得。
假设数据项A的三个副本分别存储在不同的物理节点,在某一时刻,系统状态如下图所示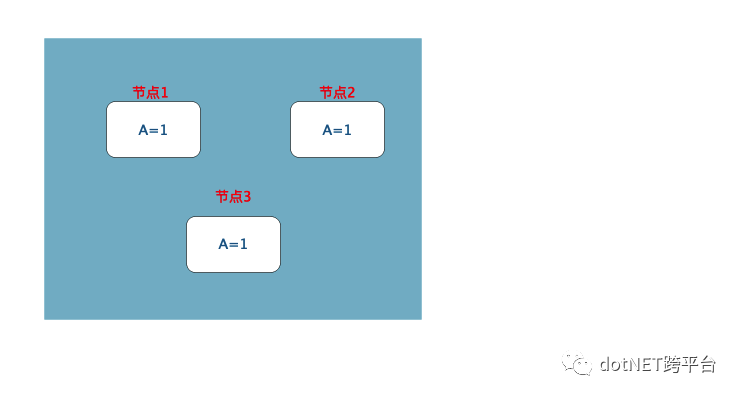

当客户端将节点1上的A修改为2后,系统出现了网络分区,其中节点1和节点2在一个网络分区中,而节点3在另一个分区中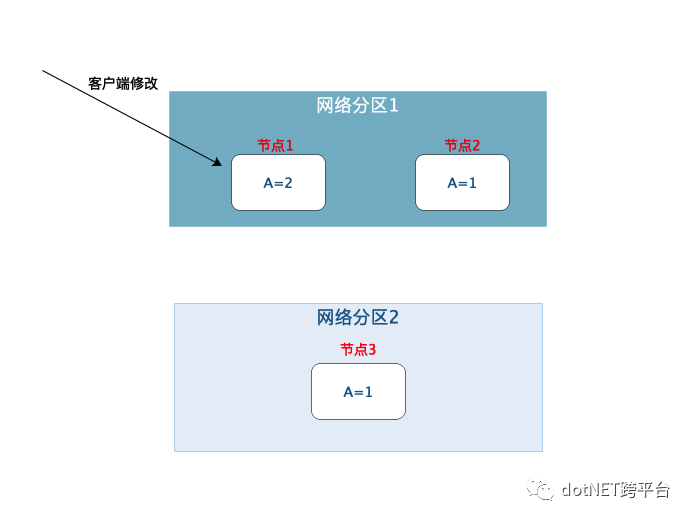

当有客户端尝试读取节点3上的A值时,系统将面临两难困境

• 系统等待节点3从节点1同步A的值,待数据一致后再返回客户端响应,但是因为节点3和节点1不在一个分区中,双方无法进行通信,导致系统无法在限定时间内给客户端返回读取结果,这明显不符合可用性的要求。

• 系统立即返回一个A=1的旧值给客户端,由于A的值在不同节点上不一样,导致一致性的条件被破坏。

因而,对于满足分区容错性的系统而言,强一致性和可用性的要求难以同时被满足。其实这是很容易理解的,即使没有网络分区,因为不同节点上的数据需要经过网络通信来保持一致性,这个过程本身就比较花时间,当需要在给定很短的时限内基于客户端响应时,对于一致性的保证自然就比较弱。

3.2 如何正确理解CAP定理

• 对于分布式系统而言CAP三要素不可兼得,但并不意味着在任何时刻都必须从中做出取舍,或者在构建分布式系统之初就选择其中两个而放弃另一个,这种看法具有片面性。

• 由于网络分区出现的可能性非常小,系统在正常运行的情况下还是应该兼顾AC两者,在进入网络分区模式后才需要对P进行保证,从A和C中选择牺牲一个。

• A和C并不是一个硬币的两面,只能选择其中一个;A和C应该看成天平,系统可以选择向哪边倾斜,但另一边也应该一定程度的保留。

• 对于A和C之间的选择,不应该粗粒度的整个系统级别进行选取,而应该针对系统中的不同子系统,针对性的采取不同的取舍策略。

4. 一致性的妥协——最终一致性和Base原则

由CAP定理可知,在分布式系统中过于追求数据的强一致性将导致可用性一定程度被牺牲,这意味着系统将不能很好的响应用户的请求,这会一定程度影响用户体验。因而对于大部分布式系统而言,应当在保证系统高可用的前提下去追求数据的一致性,BASE原则正是对这一思想的描述。

• BA(Basically Available)
  基本可用:系统在绝大部分时间应处于可用状态,允许出现故障损失部分可用性,但保证核心可用。

• S(Soft State)
  软状态:数据状态不要求在任何时刻都保持一致,允许存在中间状态,而该状态不影响系统可用性。对于多副本的存储系统而言,就是允许副本之间的同步存在延时,并且在这个过程中系统依旧可以响应客户端请求。

• E(Eventual Consistency)
  最终一致性:尽管软状态不要求分布式数据在任何时刻都保持一致,但经过一定时间后,这些数据最终能达到一致性状态。

BASE理论的核心思想是:把分布式系统的可用性放在首位,放弃CAP中对数据强一致性的追求,只要系统能保证数据最终一致。

4.1 CAP,BASE以及ACID的关系

CAP描述了对于一个分布式系统而言重要的三要素:数据一致性,可用性,分区容错性之间的制约关系,当你选择了其中的两个时,就不得不对剩下的一个做一定程度的牺牲。BASE和ACID都可以看做是对CAP三要素进行取舍后的某种特殊情况

• BASE强调可用性和分区容错性,放弃强一致性,这是大部分分布式系统的选择,比如NoSQL系统,微服务架构下的分布式系统

• ACID是单机数据的事务特性,因为不是分布式系统无需考虑分区容错,故而是选择了可用性和强一致性后的结果。
  它们之间的关系如下所示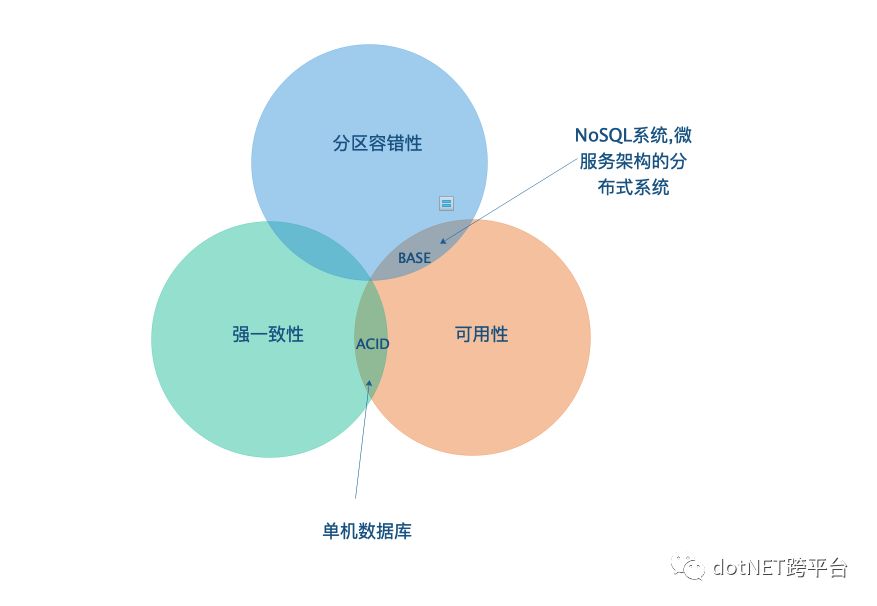
  

5. 分布式系统的幂等性

幂等的概念来自于抽象代数,比如对于一元函数来说,满足以下条件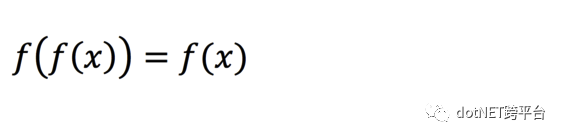

即可称为满足幂等性。在计算机科学中,一个操作如果多次执行产生的影响与一次执行的影响相同,这样的操作即符合幂等性。在分布式系统中,服务消费方调用服务提供方的接口,多次调用的结果应该与一次调用的结果一样,这正是分布式环境下幂等性的语义。为什么幂等性对分布式系统而言如此重要？因为在分布式环境下,服务的调用一般采用http协议或者rpc的方式,即双方需要通过网络进行通信,而因为网络故障或者消息超时的存在,可能服务消费方已经成功调用了服务提供方的服务接口,但是消费方并没有收到来自对方的成功响应,导致消费方以为服务调用失败从而再次进行调用,也就是说网络的不可靠性导致了服务接口被多次调用的可能。分布式系统必须保证在这种情况下,即使接口被多次调用,它对系统产生的影响应该与该接口只被调用一次的结果一样。

6.微服务架构的分布式一致性和幂等性问题

6.1 微服务架构下的分布式一致性问题

微服务架构下,处理一个业务请求可能需要调用多个微服务进行处理,以前面的下单并支付场景为例,完成该业务请求需要先后调用订单微服务的下单接口和支付微服务的支付接口,只有这两个接口都调用成功,该业务操作才算执行成功。那么微服务架构中是如何保证同属于一个业务单元的多个操作的原子性以及保证分布式数据一致性的?——答案是分布式事务。

分布式事务是指事务的参与者、支持事务的服务器、资源服务器以及事务管理器分别位于不同的分布式系统的不同节点之上

并且根据遵循的一致性原则不同,可以分为刚性分布式事务和柔性分布式事务两大类。

• 遵循ACID原则的刚性事务
  刚性事务追求数据的强一致性,比如基于两阶段提交和三阶段提交的分布式事务就属于刚性事务,通过分布式事务,客户端可以看到描述业务执行状态的多个数据的一致性视图,比如下单并支付这个业务操作,客户端要么能够同时查询到下单和支付成功的信息,要么能够同时查询到下单和支付失败的信息,其他不一致的情况对于客户端而言都是不可见的。比如下单成功,支付还在处理;下单成功,支付失败,下单记录正在回滚。也就是说,当订单数据和支付数据不一致时,对于客户端的访问请求应该予以拒绝。
  

这当然导致了系统可用性的降低,加上刚性事务实现时会导致同步阻塞的问题,锁定资源等问题,会极大的影响系统的吞吐量和设计弹性,所以实际上微服务架构不太会采用刚性事务。

• 遵循BASE原则的柔性事务
  柔性事务只对数据的最终一致性进行保证,允许系统存在一定时间的数据不一致,比如订单记录已经被更新但是支付记录还没落地时,又比如订单记录更新成功但是支付失败订单记录回滚的过程。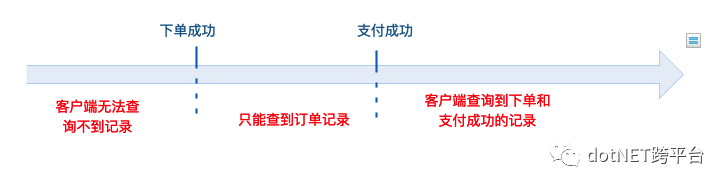
  

在这个不一致窗口内,系统允许客户端对不一致的数据进行访问,因而系统的可用性相比而言会更好,加上其扩展性良好以及吞吐量的优势,一般微服务架构下都会采用柔性事务。柔性事务有多种不同的实现方式,比如基于可靠事件的模式,基于补偿的模式,基于Sagas长事务的模式等,具体的实现原理以及优缺点对比就放到下一篇在详解解释。

6.2 微服务架构下的幂等性问题

6.2.1 幂等性场景

在微服务架构下,不同微服务间会有大量的基于http,rpc或者mq消息的网络通信,接口的重复调用以及消息的重复消费可能会经常发生,比如以下这些情况

• 调用订单创建接口,第一次调用超时,调用方又尝试了一次,但其实第一次调用已经成功,只是调用方没有及时收到响应。

• 订单支付完成后,需要向MQ发送一条消息,但该消息重复发送了两条。

• 网络波动导致服务提供方的接口被调用了两次。

• 用户在使用产品时,无意地触发多笔交易。

• 某些未关闭的重试机制。

微服务架构应该具有幂等性,当接口被重复调用时,消息被重复消费时,对系统的产生的影响应该和接口被调用一次,消息被消费一次时一样。

6.2.2 CRUD操作的幂等性分析

• 新增请求:不具备幂等性

• 查询请求:重复查询不会影响系统状态,查询天然具备幂等性

• 基于主键的更新请求
  要更新的值依赖于前值,不具备幂等性。比如update goods set number=number-1 where id=1
  要更新的值不依赖于前值,具备幂等新。比如update goods set number=newNumber where id=1

• 删除请求
  基于主键的物理删除(delete)删除具备幂等性
  基于主键的逻辑删除(update)也具有幂等性

总结:通常只需要对新增请求和更新请求作幂等性保证。

6.2.3 如何解决幂等性问题

• 全局唯一ID
  根据业务生成一个全局唯一ID,在调用接口时会传入该ID,接口提供方会从相应的存储系统比如Redis中去检索这个全局ID是否存在,如果存在则说明该操作已经执行过了,将拒绝本次服务请求;否则将相应该服务请求并将全局ID存入存储系统中,之后包含相同业务ID参数的请求将被拒绝。

• 去重表
  这种方法适用于在业务中有唯一标识的插入场景。比如在支付场景中,一个订单只会支付一次,可以建立一张去重表,将订单ID作为唯一索引。把支付并且写入支付单据到去重表放入一个事务中,这样当出现重复支付时,数据库就会抛出唯一约束异常,操作就会回滚。这样保证了订单只会被支付一次。

• 多版本并发控制
  适合对更新请求作幂等性控制,比如要更新商品的名字,这是就可以在更新的接口中增加一个版本号来做幂等性控制

boolean updateGoodsName(int id,String newName,int version);

数据库更新的SQL语句如下

update goods set name=#{newName},version=#{version} where id=#{id} and version<${version}

• 状态机控制
  适合在有状态机流转的情况下,比如订单的创建和付款,订单的创建肯定是在付款之前。这是可以添加一个int类型的字段来表示订单状态,创建为0,付款成功为100,付款失败为99,则对订单状态的更新就可以这样表示

update order set status=#{status} where id=#{id} and status<#{status}

• 插入或更新
  在MySQL数据库中，如果在insert语句后面带上ON DUPLICATE KEY UPDATE 子句，而要插入的行与表中现有记录的惟一索引或主键中产生重复值,则对旧行进行更新;否则执行新纪录的插入。
  我们可以利用该特性防止记录的重复插入,比如good_id和category_id构成唯一索引,则重复执行多次该SQL,数据库中也只会有一条记录。

insert into goods_category (goods_id,category_id,create_time,update_time) values(#{goodsId},#{categoryId},now(),now()) on DUPLICATE KEY UPDATEupdate_time=now()

7. 参考资料

《大数据日知录》
《微服务设计原理与架构》
如何保证微服务接口的幂等性

原文地址:https://www.cnblogs.com/takumicx/p/10021538.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com