传送门.

解析

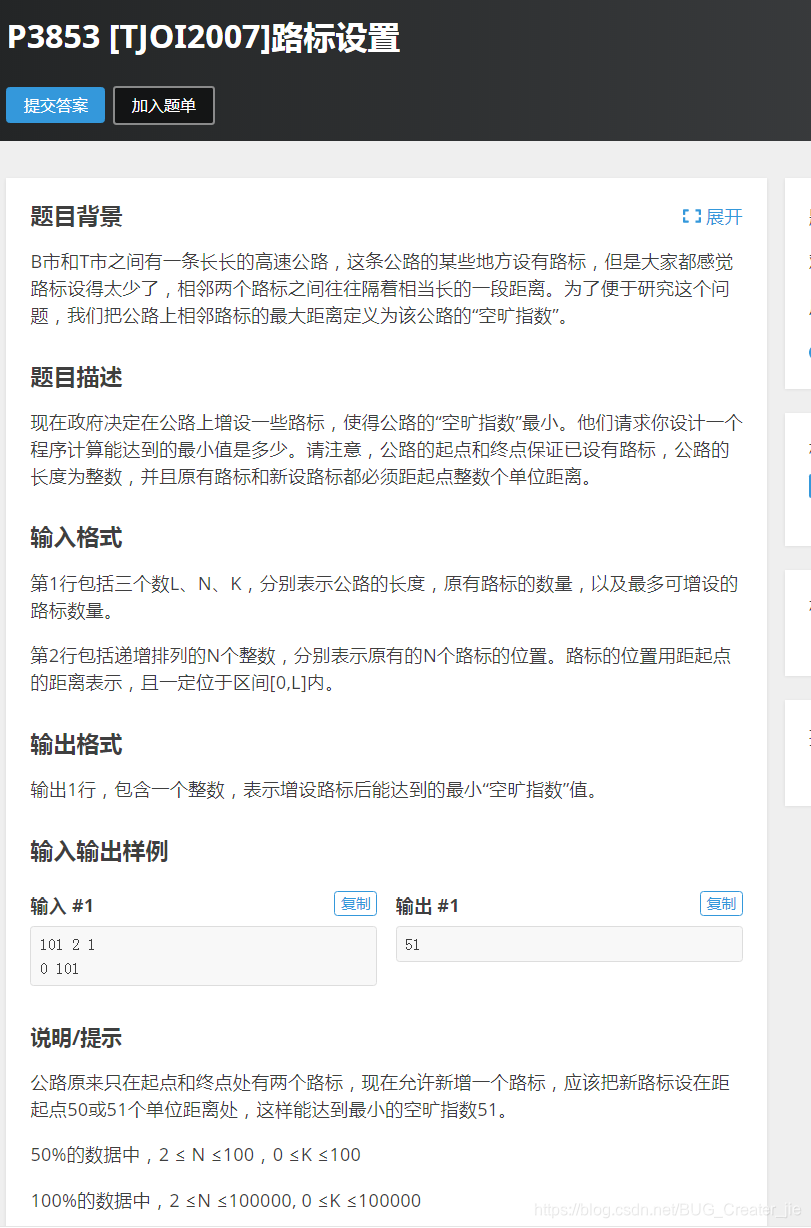
只需二分枚举空旷指数即可
对于单次判断的check函数，可以相当于n个路标把路面分成n+1个间隔，而对于每个间隔[l,r]和空旷指数x（边界已有路标），所需路标应为：

(r-l-1)/x

（比如[2,5],x=3,显然不用，所以需减1）
这样每段复杂度为O（1）
check复杂度则为O（N）
可以得到解决

update on 2022.3.17

感谢 @沉迷小说 提出的关于二分上界的问题，只需要赋值为 $l$ 即可，已经修正

代码

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<string>
#include<queue>
#include<vector>
using namespace std;
const int M=1e9;
int l,n,k;
int a[100500]={ },d[100500];
bool check(int x){int num=0;for(int i=1;i<=n+1;i++){num+=(d[i]-1)/x;}return num<=k;
}
int main(){scanf("%d%d%d",&l,&n,&k);a[0]=1;for(int i=1;i<=n;i++){scanf("%d",&a[i]);d[i]=a[i]-a[i-1];//记录每段间隔长度}d[n+1]=l-a[n];int st=0,ed=l;while(st<ed){int mid=(st+ed) >> 1;if(check(mid)) ed=mid;else st=mid+1;}printf("%d",st);return 0;
}

AC快乐！！！