P2486 [SDOI2011]染色

题意：

题解：

与一般的树链剖分相比，不同点在于查询的不是路径上颜色的数量而是颜色段的数量
对于两个颜色段，112和221，两个颜色段数量都是2
如果合在一起颜色段的数量就是3，因为左边颜色段的右侧和右边颜色段的左侧是一样的颜色，合在一起后就成一段
所以本题其实就是将常规的区间求和改成这种特殊情况，在求完和的基础上，对左区间的最后一个颜色和右区间的第一个颜色进行判断，如果一样就减一

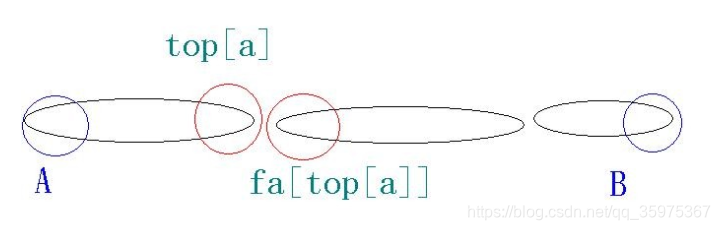
树剖中是把两点之间剖成了若干条链，所以我们还要解决不同的链之间的颜色重复问题，解决top[a]与fa[top[a]]颜色重复问题即可（如图）

总结一下：
就是判断所有接口处颜色是否一样

代码：

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define lid (id << 1)
#define rid (id << 1) | 1
using namespace std;
int read(){int out = 0,flag = 1;char c = getchar();while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}return flag * out;}
const int maxn = 100019;
int num,na,nume,cnt;
int head[maxn];
struct Node{int v,nxt;
}E[maxn * 2];
void add(int u,int v){E[++nume].nxt = head[u];E[nume].v = v;head[u] = nume;}
int size[maxn],wson[maxn],dep[maxn],fa[maxn],top[maxn],pos[maxn],ori[maxn];
int col[maxn];
void dfs1(int id,int F){size[id] = 1;for(int i = head[id];i;i = E[i].nxt){int v = E[i].v;if(v == F)continue;dep[v] = dep[id] + 1;fa[v] = id;dfs1(v,id);size[id] += size[v];if(size[v] > size[wson[id]])wson[id] = v;}
}
void dfs2(int id,int TP){top[id] = TP;pos[id] = ++cnt;ori[cnt] = id;if(!wson[id])return ;dfs2(wson[id],TP);for(int i = head[id];i;i = E[i].nxt){int v = E[i].v;if(v == fa[id] || v == wson[id])continue;dfs2(v,v);}
}
int lc[maxn << 2];
int rc[maxn << 2];
struct sag_tree{int l,r;int sum,c;//区间颜色总数，叶子颜色int lazy;//儿子的颜色
}tree[maxn << 2];
void pushup(int id)
{tree[id].sum = tree[lid].sum + tree[rid].sum;if(rc[lid] == lc[rid])tree[id].sum -= 1;//如果连接处颜色一样，减一 lc[id] = lc[lid];rc[id] = rc[rid];
} 
void build(int id,int l,int r){tree[id].l = l;tree[id].r = r;if(l == r){tree[id].c = col[ori[l]];//赋值：叶子颜色lc[id] = rc[id] = col[ori[l]];//赋值：区间左颜色和区间右颜色tree[id].sum = 1;//颜色数为1return ;}int mid = l + r >> 1;build(lid,l,mid);build(rid,mid + 1,r);pushup(id);
}
void pushdown(int id){if(tree[id].lazy != 0 && tree[id].l != tree[id].r){int c = tree[id].lazy;tree[lid].lazy = tree[rid].lazy = c;//粉刷tree[lid].c = tree[rid].c = c;lc[lid] = rc[lid] = lc[rid] = rc[rid] = c;//更新左右tree[lid].sum = tree[rid].sum = 1;//粉刷完以后只有一种颜色了tree[id].lazy = 0;}
}
void update(int id,int c,int l,int r){pushdown(id);if(tree[id].l == l && tree[id].r == r){tree[id].c = c;//更新颜色 tree[id].lazy = c;tree[id].sum = 1;//此时区间内只有一种颜色  lc[id] = rc[id] = c;return ;}int mid = tree[id].l + tree[id].r >> 1;if(mid < l){update(rid,c,l,r);}else if(mid >= r){update(lid,c,l,r);}else{update(lid,c,l,mid);update(rid,c,mid + 1,r);}pushup(id);
}
int query(int id,int l,int r)//查询区间颜色数量 
{pushdown(id);if(tree[id].l == l && tree[id].r == r){return tree[id].sum;}int mid = tree[id].l + tree[id].r >> 1;if(mid < l){return query(rid,l,r);}else if(mid >= r){return query(lid,l,r);}else{int ret = query(lid,l,mid) + query(rid,mid + 1,r);if(rc[lid] == lc[rid])ret -= 1;//如果连接处颜色一样 return ret;}
}
int Qc(int id,int l,int r){//查询单点的颜色pushdown(id);if(tree[id].l == l && tree[id].r == r){return tree[id].c;}int mid = tree[id].l + tree[id].r >> 1;if(mid < l)return Qc(rid,l,r);else return Qc(lid,l,r);
}
void uprange(int x,int y,int c){while(top[x] != top[y]){if(dep[top[x]] < dep[top[y]])swap(x,y);update(1,c,pos[top[x]],pos[x]);x = fa[top[x]];}if(dep[x] > dep[y])swap(x,y);update(1,c,pos[x],pos[y]);
}
int Qsum(int x,int y){int ans = 0,Cson,Cfa;//儿子的颜色，爸爸的颜色while(top[x] != top[y]){if(dep[top[x]] < dep[top[y]])swap(x,y);ans += query(1,pos[top[x]],pos[x]);Cson = Qc(1,pos[top[x]],pos[top[x]]);Cfa = Qc(1,pos[fa[top[x]]],pos[fa[top[x]]]);if(Cson == Cfa)ans -= 1;x = fa[top[x]];}if(dep[x] > dep[y])swap(x,y);ans += query(1,pos[x],pos[y]);return ans;
}
int main(){num = read();na = read();for(int i = 1;i <= num;i++)col[i] = read();int u,v;for(int i = 1;i <= num - 1;i++){u = read();v = read();add(u,v);add(v,u);}dfs1(1,-1);dfs2(1,1);build(1,1,num);char ask;int c;for(int i = 1;i <= na;i++){cin>>ask;if(ask == 'Q'){u = read();v = read();printf("%d\n",Qsum(u,v));}else{u = read();v = read();c = read();uprange(u,v,c);}}return 0;}