T1：一个简单的询问

题目

给你一个长度为 N 的序列 ai ,1≤i≤N，和 q 组询问，每组询问读入 l1,r1,l2,r2，需输出
$\infty$
$\sum get(l1,r1,x)\cdot get(l2,r2,x)$
$x=0$
get(l,r,x) 表示计算区间 [l,r] 中，数字 x 出现了多少次。

输入格式
第一行，一个数字 N，表示序列长度。
第二行，N 个数字，表示 a1∼aN
第三行，一个数字 Q，表示询问个数。
第 4∼Q+3 行，每行四个数字 l1,r1,l2,r2，表示询问。
输出格式
对于每组询问，输出一行一个数字，表示答案。

输入输出样例
输入
5
1 1 1 1 1
2
1 2 3 4
1 1 4 4
输出
4
1
说明/提示
对于20% 的数据，1≤N,Q≤1000；
对于另外 30% 的数据，1≤ai≤50；
对于 100% 的数据，N,Q≤50000，1≤ai≤N，1≤l1≤r1≤N，1≤l2≤r2≤N

答案有可能超过 int 的最大值

题解

首先对于一个区间，我们考虑对它进行转化，使用差分
$get(l,r,x)=get(1,r,x)-get(1,l-1,x)$
那么答案也就可以转化为
$$\sum _{x=0}^{\infty }get(l1,r1,x)\cdot get(l2,r2,x)$$
$$\Downarrow$$
$$\sum _{x=0}^{\infty }[get(1,r1,x)-get(1,l1-1,x)]\ast [get(1,r2,x)-get(1,l2-1,x)]$$
$$\Downarrow$$
$$\sum _{x=0}^{\infty }get(1,r1,x)\ast get(1,r2,x)-get(1,r1,x)\ast get(1,l2-1,x)$$
$$-get(1,l1-1,x)\ast get(1,r2,x)+get(1,l1-1,x)\ast get(1,l2-1,x)$$

---

之后我们把它拆成四个询问块，再用一个sign记录前面的符号±
1.$get(1,r1,x)\ast get(1,r2,x)(+)$
2.$get(1,r1,x)\ast get(1,l2-1,x)(-)$
3.$get(1,l1-1,x)\ast get(1,r2,x)(-)$
4.$get(1,l1-1,x)\ast get(1,l2-1,x)(+)$

---

最后我们来考虑算法以及转移过程
因为这个并没有要求强制在线，其次它只有多个区间查询，并没有涉及到更新
所以莫队就相较于线段树更加适合，线段树有点大材小用了
$$get(1,r,x)\ast get(1,l+1,x)=get(1,l,x)\ast get(1,r,x)+sum$$
sum表示a[l]在[1,r]区间出现的次数
为森么是这样的呢？？
我们思考除开a[l]，其它值出现次数并未发生改变，所以对答案的影响也并没有改变
当l+1，就意味着多加了一个get(1,r,x)，即
$$get(1,r,x)\ast get(1,l+1,x)=[get(1,l,x)+get(l+1,l+1,x)]\ast get(1,r,x)$$
那么同理r进行移动的时候，就要加减a[r]在[1,l]区间内出现的次数

故，我们用两个cntl[i]，cntr[i]分别表示i在[1,l]出现的次数和i在[1,r]出现的次数

---

这里用的莫队算法，跟平常不太一样，平时是用于维护[l,r]区间，
而这里我们维护是是[1,l]和[1,r]

代码实现

#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
#define MAXN 50005
struct node {int id, l, r, sign, num;
}query[MAXN << 2];
int n, q, tot, sum;
int a[MAXN], cntl[MAXN], cntr[MAXN];
int result[MAXN];bool cmp ( node x, node y ) {return x.num == y.num ? x.r < y.r : x.num < y.num; 
}int main() {scanf ( "%d", &n );for ( int i = 1;i <= n;i ++ )scanf ( "%d", &a[i] );scanf ( "%d", &q );int T = ( int ) sqrt ( double ( n ) );for ( int i = 1;i <= q;i ++ ) {int l1, r1, l2, r2;scanf ( "%d %d %d %d", &l1, &r1, &l2, &r2 );query[++ tot] = ( node ) { i, r1, r2, 1, r1 / T };query[++ tot] = ( node ) { i, l1 - 1, r2, -1, ( l1 - 1 ) / T };query[++ tot] = ( node ) { i, l2 - 1, r1, -1, ( l2 - 1 ) / T };query[++ tot] = ( node ) { i, l1 - 1, l2 - 1, 1, ( l1 - 1 ) / T };}sort ( query + 1, query + tot + 1, cmp );int curl = 0, curr = 0;for ( int i = 1;i <= tot;i ++ ) {int l = query[i].l, r = query[i].r;while ( l < curl ) {cntl[a[curl]] --;sum -= cntr[a[curl]];curl --;}while ( l > curl ) {curl ++;cntl[a[curl]] ++;sum += cntr[a[curl]];}while ( r < curr ) {cntr[a[curr]] --;sum -= cntl[a[curr]];curr --;}while ( curr < r ) {curr ++;cntr[a[curr]] ++;sum += cntl[a[curr]];}result[query[i].id] += sum * query[i].sign;}for ( int i = 1;i <= q;i ++ )printf ( "%d\n", result[i] );return 0;
} 

T2：愤怒的小鸟

题目

Kiana 最近沉迷于一款神奇的游戏无法自拔。
简单来说，这款游戏是在一个平面上进行的。
有一架弹弓位于 (0,0) 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如 y=ax^2+bx的曲线，其中 a,b是Kiana 指定的参数，且必须满足 a < 0,a,b 都是实数。
当小鸟落回地面（即 x 轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有 n 只绿色的小猪，其中第 i 只小猪所在的坐标为(xi,yi)
如果某只小鸟的飞行轨迹经过了(xi,yi)，那么第 i 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；
如果一只小鸟的飞行轨迹没有经过 (xi,yi)，那么这只小鸟飞行的全过程就不会对第 i 只小猪产生任何影响。
例如，若两只小猪分别位于 (1,3)和 (3,3)，Kiana 可以选择发射一只飞行轨迹为 y=-x^2+4x的小鸟，这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对 Kiana来说都很难，所以Kiana还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。
假设这款游戏一共有 TT 个关卡，现在 Kiana想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

输入格式
第一行包含一个正整数 T，表示游戏的关卡总数。
下面依次输入这 T 个关卡的信息。每个关卡第一行包含两个非负整数 n,m，分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 n 行中，第 i行包含两个正实数xi,yi表示第 i 只小猪坐标为 (xi,yi)数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果 m=0，表示Kiana输入了一个没有任何作用的指令。
如果 m=1，则这个关卡将会满足：至多用⌈n/3+1⌉ 只小鸟即可消灭所有小猪。
如果 m=2，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少⌊n/3⌋ 只小猪。
保证1≤n≤18，0≤m≤2，0 <xi,yi < 100输入中的实数均保留到小数点后两位。

上文中，符号⌈c⌉ 和⌊c⌋ 分别表示对 c 向上取整和向下取整，例如：⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。
输出格式
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

输入输出样例
输入
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00
输出
1
1

输入
3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00
输出
2
2
3

输入
1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99
输出
6

说明/提示
【样例解释1】
这组数据中一共有两个关卡。
第一个关卡与【问题描述】中的情形相同，2只小猪分别位于(1.00,3.00)和 (3.00,3.00)，只需发射一只飞行轨迹为y = -x^2 + 4x的小鸟即可消灭它们。
第二个关卡中有5只小猪，但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6x上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【数据范围】

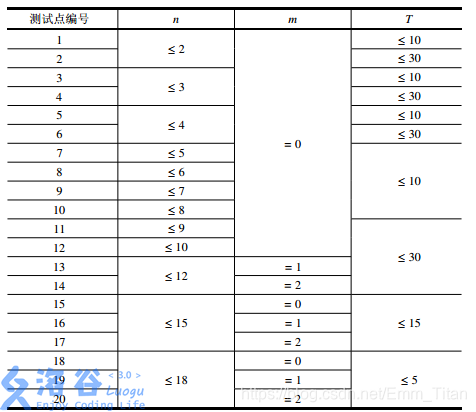
暴搜题解

首先就是计算两个点的抛物线解析式（在状压题解中我就不再阐释）
y1=a1*x²+ b1*x
y2=a2*x²+b2*x
可以先把a算出来，也就得把b1，b2消掉，那么方程式分别乘上另一个方程式b的系数
再两式一减，把x移过去就可以了，即
b2*y1=a1*b2*x²+ b1*b2*x
b1*y2=a2*b1*x²+b1*b2*x

---

暴力的思路就是遍历每一只猪，在当前状态下已经用了多少只鸟（抛物线）
有多少只猪猪是一只猪孤单的死去
那么答案就是用的鸟的个数加上单独的猪的个数
1.猪猪可以多个匹配被一只鸟一次性杀死
2.猪太特殊了，只能单独找一鸟抵着它杀

那我们就枚举每一个猪猪的状态，单独被杀，或者和前后面的某些猪一起被杀

---

部分阐释在代码中有呈现

暴搜代码实现

#include <cmath>
#include <cstdio>
#define MAXN 20
int T, n, m, result;
double x[MAXN], y[MAXN];
double tx[MAXN], ty[MAXN];
double pwxa[MAXN], pwxb[MAXN];bool check ( double a, double b ) {return fabs ( a - b ) < 1e-7;
}void dfs ( int pig, int used, int alone ) {if ( used + alone >= result )//最优性剪枝，因为在这样下去//1.抛物线的个数+1，少了一只单独的猪-1，并不会使答案变小//2.猪仔之前与别的猪一起被一条抛物线经过了，就掠过它，答案也没有变//3.猪单独被一条抛物线经过+1，答案反而大了//所以这种时候往下搜索最多就是保持不变，一定大于当前最佳答案，就没有必要搜索了return;if ( pig > n ) {result = used + alone;return;}bool flag = 0;for ( int i = 1;i <= used;i ++ ) {//判断之前构造的抛物线有没有一条经过了这只猪if ( check ( pwxa[i] * x[pig] * x[pig] + pwxb[i] * x[pig], y[pig] ) ) {dfs ( pig + 1, used, alone );flag = 1;break;}}if ( ! flag ) {//看能不能把这只猪和单身的猪组个队一起死for ( int i = 1;i <= alone;i ++ ) {//特殊判断，如果x相同意味着，这是一条常函数，是不可能一起死的if ( check ( tx[i], x[pig] ) )continue;double a = ( y[pig] * tx[i] - ty[i] * x[pig] ) / ( x[pig] * x[pig] * tx[i] - tx[i] * tx[i] * x[pig] );double b = ( y[pig] - x[pig] * x[pig] * a ) / x[pig];if ( a < 0 ) {//要小于零才是匹配的组队pwxa[used + 1] = a;pwxb[used + 1] = b;double Ai = tx[i], Bi = ty[i];//这只猪已经和本层循环的猪配对了，就要把它踢出单身狗群体for ( int j = i;j < alone;j ++ ) {tx[j] = tx[j + 1];ty[j] = ty[j + 1];}dfs ( pig + 1, used + 1, alone - 1 );//回溯后，这只猪重获单身for ( int j = alone;j > i;j -- ) {ty[j] = ty[j - 1];tx[j] = tx[j - 1];}tx[i] = Ai;ty[i] = Bi;}}//本层循环的猪也加入单身行列tx[alone + 1] = x[pig];ty[alone + 1] = y[pig];dfs ( pig + 1, used, alone + 1 );}
}int main() {scanf ( "%d", &T );while ( T -- ) {result = 0x7f7f7f7f;scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ )scanf ( "%lf %lf", &x[i], &y[i] );dfs ( 1, 0, 0 );printf ( "%d\n", result );}return 0;
} 

状压DP题解

n≤18，在暴搜基础上我们就可以考虑状压DP
0表示这只猪还活着，1表示这只猪仔已经被鸟干死了

---

首先我们还是暴力跑个n²，去求出以任意两只猪构造一条抛物线，一次性能杀死多少猪
接着就是常规的状态转移了$DP[s]$表示当状态为s时，所用的最少抛物线个数
当s状态时枚举每一条抛物线与s进行或运算，有可能开始s就已经杀了某只猪
而这条抛物线让猪猪重复死亡了罢了
$$DP[s|pwx[i][j]]=min(DP[s|pwx[i][j],DP[s]+1)$$

---

此处还可以有一个优化
我们想一想如果pwx能打1，2，4，7，它会傻着先把后面的4,7杀了再跑回来搞1,4？
肯定是一路上不走回头路，不打回头猪啊！
所以我们就开一个数组记录当状态为s时最先打到的猪仔是谁

状压DP代码实现

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define eps 1e-7
#define MAXN 20
int n, m, T;
double x[MAXN], y[MAXN];
int pwx[MAXN][MAXN], dp[1 << MAXN];
int lowcount[1<< MAXN];bool check ( double u, double v ) {return fabs ( u - v ) < eps;
}void count ( double &a, double &b, double x1, double y1, double x2, double y2 ) {a = ( y1 * x2 - y2 * x1 ) / ( x1 * x1 * x2 - x2 * x2 * x1 );b = ( y1 - x1 * x1 * a ) / x1;
}int main() {for ( int i = 0;i < ( 1 << 18 );i ++ ) {int j = 1;while ( ( i & ( 1 << ( j - 1 ) ) ) && j <= 18 )j ++;lowcount[i] = j;}scanf ( "%d", &T );while ( T -- ) {scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ )scanf ( "%lf %lf", &x[i], &y[i] );memset ( dp, 0x7f, sizeof ( dp ) );memset ( pwx, 0, sizeof ( pwx ) );dp[0] = 0; for ( int i = 1;i <= n;i ++ ) {for ( int j = 1;j <= n;j ++ ) {if ( x[i] == x[j] )continue;double a, b;count ( a, b, x[i], y[i], x[j], y[j] );if ( a >= 0 ) continue;for ( int k = 1;k <= n;k ++ )if ( check ( a * x[k] * x[k] + b * x[k], y[k] ) )	pwx[i][j] |= ( 1 << ( k - 1 ) );}}for ( int i = 0;i < ( 1 << n );i ++ ) {int j = lowcount[i];dp[i | ( 1 << ( j - 1 ) )] = min ( dp[i | ( 1 << ( j - 1 ) )], dp[i] + 1 );for ( int k = 1;k <= n;k ++ )dp[i | pwx[j][k]] = min ( dp[i | pwx[j][k]], dp[i] + 1 );}printf ( "%d\n", dp[( 1 << n ) - 1] );} return 0;
} 

走了，如有疑问欢迎评论，欢迎指出错误