CF468C Hack it!
题意:
令 \(F(x)\) 表示 \(x\) 的各个位上的数字之和,如 \(F(1234)=1+2+3+4=10\) 。
给定 \(a(a\le 10^{18})\) ,请求出任意一组 \(l,r(l,r\le 10^{200})\) ,要求满足:
输出 \(l,r\) 。
$\texttt{solution}$
注意到,若 \(F(x)=p\) ,那么 \(F(x+10^{18})=F(x)+1=p+1\) 。
那么可以发现,若 \(\sum_{i=0}^{10^{18}-1}F(i)=p\) ,那么有:
因此发现 \(l=a-p,r=a-p+10^{18}-1\) 时恰好能够成立。
因此考虑求出 \(p\) 。
之后带入式子就可以啦!
typedef unsigned long long ll;
ll a,l,r,p,inf=1e18;
int main()
{a=rd(),p=inf%a*9llu%a*9llu%a;printf("%llu %llu\n",a-p,a-p+inf-1llu);return 0;
}CF1491F Magnets
交互、二分。
早苗有 \(n\) 块磁石,编号为 \(1,2,\cdots,n\)。每块磁石的磁极可能是正极,负极,也可能没有磁性。她希望你能帮她找出所有没有磁性的磁石。
万幸的是,你有一台磁力检测仪。你每次可以将每个磁石放在这台机器的左托盘,右托盘或者不放。
机器将会返回此时的磁力强度。设托盘左边有 \(n_1\) 个磁石为正极,\(s_1\) 个磁石为负极,托盘右边中有 \(n_2\) 磁石为正极,\(s_2\) 个磁石为负极,则返回的磁力强度为 \(n_1n_2+s_1s_2-n_1s_2-n_2s_1\)。
如果一次测试中磁力强度的绝对值大于 \(n\),这台机器就会坏掉。
你需要在 \(n+\lfloor\log_2n\rfloor\) 次测试内找到所有没有磁性的磁石的编号,同时不能弄坏机器。
保证存在至少 \(2\) 块磁石有磁性且至少 \(1\) 块磁石没有磁性。
$\texttt{solution}$
先化简式子发现交互的返回值就是 \((n_1-s_1)(n_2-s_2)\)。
由于正负极石头放在一起会导致 \(n,s\) 会都大于 \(0\) ,使问题变得更为困难。
那么考虑每次查询只对一块石头与其他一堆石头之间进行询问。
那么如果我们已经知道了一块有磁性的此时,就可以非常容易的知道其他所有的此时是否有磁性。
之后考虑如何才能找出有磁性的石头,直接枚举肯定是不行的,最坏都会到 \(O(n^2)\) 。
我们可以从 \(1\) 向 \(n\) 开始枚举 \(i\),询问 \([1,i-1]\) 与 \(i\)。若询问结果不为 \(0\),则 \([1,i-1]\) 中必然有一块有磁性的石头,而 \(i\) 也一定是有磁性的。因此可以找出一块有磁性的石头。
之后我们是否可以 \(O(n)\) 检查所有石头了呢?还是不行。。。
考虑到答案不能超过 \(n+\log n\),所以我们只能将上面第二块石头之后,也就是 \([i+1,n]\) 中的石头判断一遍。这样到现在为止总共用了 \(n-1\) 次操作。
而 \([1,i-1]\) 中只有 \(1\) 快有磁性的石头,所以我们可以二分出这块石头的位置,找出这最后一块有磁性的石头。那么我们就做完啦。
int T,n,Last,pos,cnt;
int ans[Maxn];
inline int query(int nl,int nr,int k)
{printf("? %d %d\n",nr-nl+1,1);for(int i=nl;i<=nr;i++) printf("%d%c",i,(i==nr)?'\n':' ');printf("%d\n",k);fflush(stdout);return rd();
}
inline void print()
{printf("! %d ",cnt);for(int i=1;i<=cnt;i++) printf("%d%c",ans[i],(i==cnt)?'\n':' ');fflush(stdout);
}
int main()
{T=rd();while(T--){n=rd(),pos=-1,cnt=0;for(int i=2;i<=n && pos==-1;i++)if(query(1,i-1,i)) pos=i;for(int i=pos+1;i<=n;i++) if(!query(i,i,pos)) ans[++cnt]=i;int nl=1,nr=pos-1;while(nl<=nr){int mid=(nl+nr)>>1;if(query(1,mid,pos)) Last=mid,nr=mid-1;else nl=mid+1;}for(int i=1;i<pos;i++) if(i!=Last) ans[++cnt]=i;print();}return 0;
}CF1586F Defender of Childhood Dreams
给定一张竞赛图(点数 \(\le 1000\)),对于所有 \(a<b\),都有一条由 \(a\) 到 \(b\) 的有向边,并且每一条边都有一个颜色。现在要求所有长度大于等于 \(k\) 的路径上都有 \(\ge 2\) 中颜色。求出整张图中出现最少出现颜色的数量与边的染色方案。
$\texttt{solution}$
考虑将序列分为许多长度不超过 \(k\) 个块,在块与块间连接相同颜色的边。这样可以保证在块与块间转移的边不会形成 \(\ge k\) 长度的路径。
在每一个块内部再进行同样的拆分(但在块内的颜色要与块外的颜色不同),递归进行即可。
#define Maxn 1005
int n,k,ans;
int col[Maxn][Maxn];
void solve(int l,int r,int c)
{if(l==r) return;int len=(r-l+k)/k,tot=(r-l+len)/len;for(int i=1,x,y;i<tot;i++)for(int j=i+1;j<=tot;j++)for(int p=1;p<=len;p++)for(int q=1;q<=len;q++){x=l+(i-1)*len+p-1,y=l+(j-1)*len+q-1;if(y>r) break;col[x][y]=c;}for(int i=1;i<=tot;i++) solve(l+(i-1)*len,min(l+i*len-1,r),c+1);
}
int main()
{n=rd(),k=rd();solve(1,n,1);for(int i=1;i<n;i++) for(int j=i+1;j<=n;j++) ans=max(ans,col[i][j]);printf("%d\n",ans);for(int i=1;i<n;i++) for(int j=i+1;j<=n;j++) printf("%d ",col[i][j]);printf("\n");return 0;
}CF715D Create a Maze
有一个 \(n\times m\) 的迷宫,每一格都是一个房间,每两个相邻的房间之间有一扇门。
在所有门中,有 \(k\) 扇是锁着的,不能通行,其余没有限制。
现在你在 \((1,1)\),需要走到 \((n,m)\),只能向下或向右走。
设总共的行走方案有 \(T\) 种。
现在给出 \(T\),要求设计出一个迷宫满足行走方案为 \(T\)。
要求:\(n,m\le 50,k\le 500,T\le 10^{18}\)。
$\texttt{solution}$
这一题需要按照 \(T\) 的进制来解决问题。
首先考虑用二进制,那么我们可以这样设计方案:

这样我们就可以用二进制来表示出任何 \(\le 2^{49}\) 的 \(T\) 啦!
然而我们发现如果我们将我们的以 \(2\times 2\) 改为 \(3\times 3\),可以将前面的二进制变为六进制!!
之后构造就比较类似,我们只要改为两路 \(1\) 和中间的 \(3\times 3\) 即可。
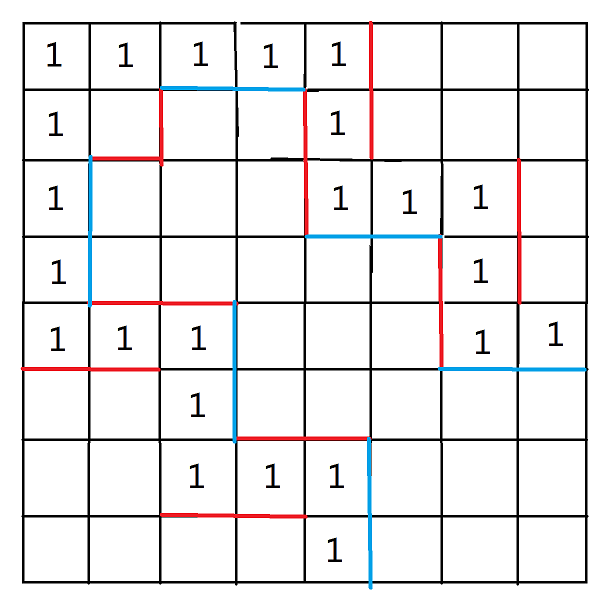
这样最大可以表示 \(6^{24}>10^{18}\),可以解决这道题啦!

![Star Way To Heaven (prim最小生成树) // [ NOIP提高组 2014]飞扬的小鸟(DP)](http://pic.xiahunao.cn/Star Way To Heaven (prim最小生成树) // [ NOIP提高组 2014]飞扬的小鸟(DP))


)
![【做题记录】[NOIP2011 提高组] 观光公交](http://pic.xiahunao.cn/【做题记录】[NOIP2011 提高组] 观光公交)
![[2019 牛客CSP-S提高组赛前集训营4题解] 复读数组(数论)+ 路径计数机(数上DP)+ 排列计数机(线段树+二项式定理)](http://pic.xiahunao.cn/[2019 牛客CSP-S提高组赛前集训营4题解] 复读数组(数论)+ 路径计数机(数上DP)+ 排列计数机(线段树+二项式定理))
哈希)
)




![[C++]试一试结构体struct node的构造函数](http://pic.xiahunao.cn/[C++]试一试结构体struct node的构造函数)


![[多校联考-西南大学附中]切面包(线段树/概率与期望)+ Slow Path Finding Algorithm(拓扑排序/DP)+ 分数转化(数论)](http://pic.xiahunao.cn/[多校联考-西南大学附中]切面包(线段树/概率与期望)+ Slow Path Finding Algorithm(拓扑排序/DP)+ 分数转化(数论))
![P3992 [BJOI2017]开车](http://pic.xiahunao.cn/P3992 [BJOI2017]开车)
)
