前言

前几年一直在写类似dubbo，Spring Cloud的微服务框架辗辗转转重复了多次，也重构推翻了很多次，其中诞生了“Rabbit.Rpc”,”Go”,”RabbitCloud”等开源项目。

其中不乏他人对这些项目的完善。很高兴自己的开源项目能够给他人提供思路和复用代码。

关于Rabbit.Rpc相关的文章：

《.NET轻量级RPC框架：Rabbit.Rpc》

《拥抱.NET Core，跨平台的轻量级RPC：Rabbit.Rpc》

挫折

但无一不被推翻。为什么呢？是因为没有耐心？喜新厌旧吗？

回顾经历，鄙人一直在互联网类型的公司就职，用户量和请求量都不算低，而自己造的轮子在具体应用上多多少少存在一些问题。

为什么不去解决遇到的问题呢？

一个人的精力有限，越深入越发现一个微服务框架需要考虑的事情太多，而不是简简单单写点代码达到展示可用。

真正用在生产上会遇到很多奇奇怪怪的需求，有技术正确的也有业务需要的。

而且每一个项目对微服务框架的需求也不尽一样。经常遇到某些功能在A处可用，在B处就没那么流利了。

是能力不足代码太low吗？

也存在这个可能。个人觉得微服务框架需要大量的微服务实践经验。或许是本人的实践经验还不够。

站在巨人的肩膀上

这时候我发现了一个项目“SteeltoeOSS”这是Spring Cloud团队在.NET下的实现。这时我准备拥抱开源，放弃自己造核心轮子的想法。利用社区的经验衍生出更方便的使用方式。

然而SteeltoeOSS因为创建不久，无法完全对标Java Spring Cloud的实现，缺少了一些快速上手的能力，比如feign（声明式API请求客户端），Hystrix的集成，ribbot（负载均衡服务器），只有基于eureka的服务发现。

这样的情况便萌生了我补缺的想法，我基于SteeltoeOSS添加了三个新的项目，分别是：steeltoe-extensions（Steeltoe.Discovery.Consul.Client，基于consul的服务发现），ribbon和feign（简单可用）。其中feign属于简单可用，耦合的比较紧，目前feign还在ribbon的git仓库。

为什么要这么做？

“.NET不缺乏轮子，而是缺乏稳定生产可用的轮子。”

目前这套解决方案只在前段时间"福州首届.NET开源社区线下技术交流会"上公开宣讲过。

这套解决方案也用于生产,不是满足私欲的花瓶框架。

下面是生产环境的相关情况：

最大峰值：80W/min

日请求量：2亿

微软官方实地勘察调研，并作为案例向社会推广.NET Core。

看看效果

首先准备2个server（服务提供方）

这边大家意会就可以了，后续会写详细的文章来一步一步完成和解释这些步骤。

配置如下：

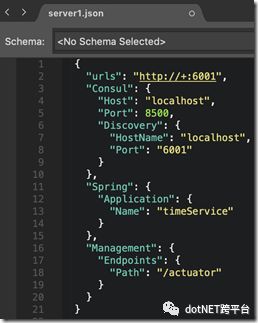
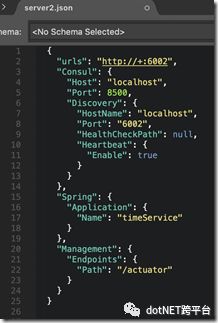
大概的意思是：

本地绑定的服务端口分别是 6001和6002

配置Consul的地址和注册到Consul上的服务地址

其中server2关闭了url健康检查（consul定时向server1请求，返回200代表健康），启用了心跳检查（定时向consul报告我还活着）。

设置服务的名称

添加actuator端点（提供健康检查等能力，来自SteeltoeOSS）

Program如下：

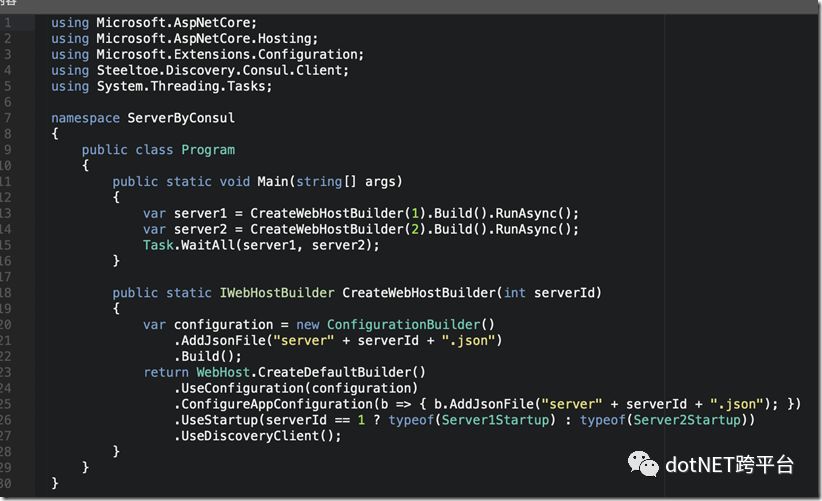
大概的意思是：

根据不同的serverId加载不同的配置文件并且创建对应的WebHost

其中UseDiscoveryClient是启用发现客户端的意图

Startup如下：

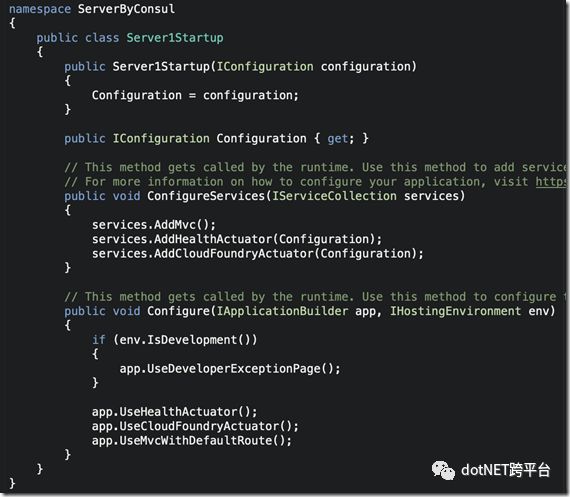
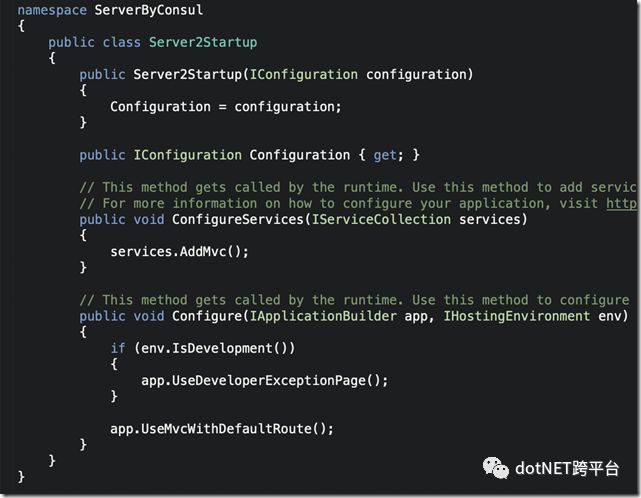
大概的意思是：

server1启用mvc，健康检查端点和CloudFoundry端点（url健康检查）

server2只启用mvc（心跳检查）

Controller如下：

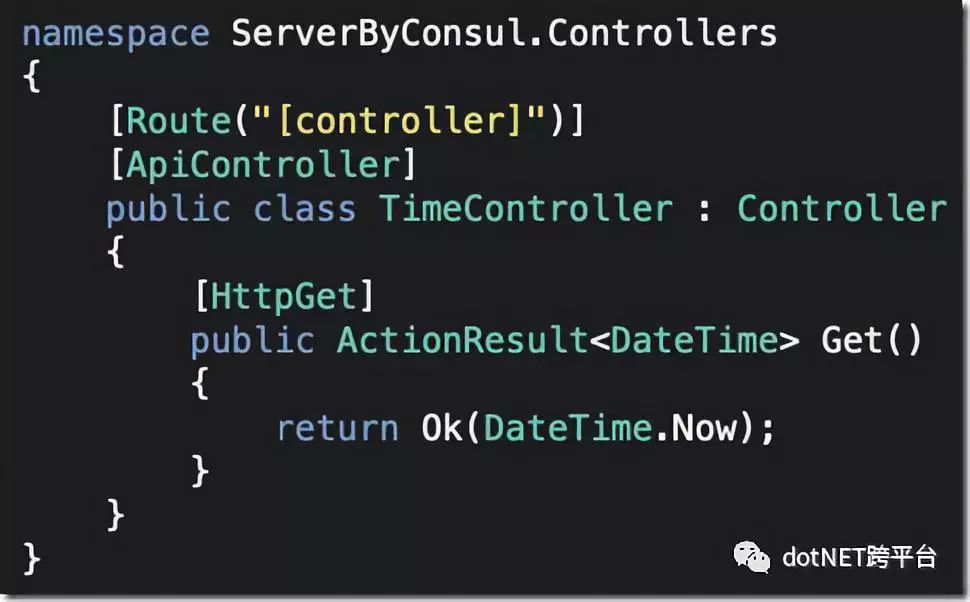
大概的意思：返回当前时间

看看Consul

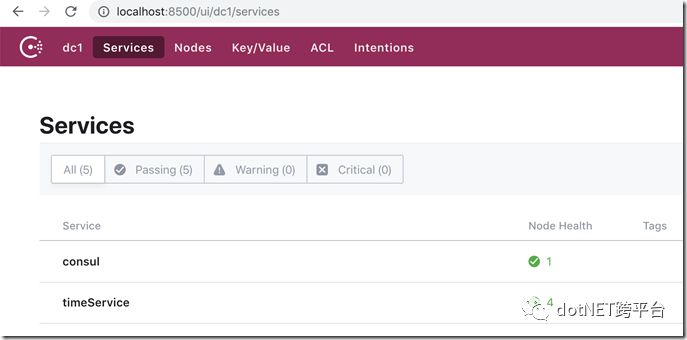
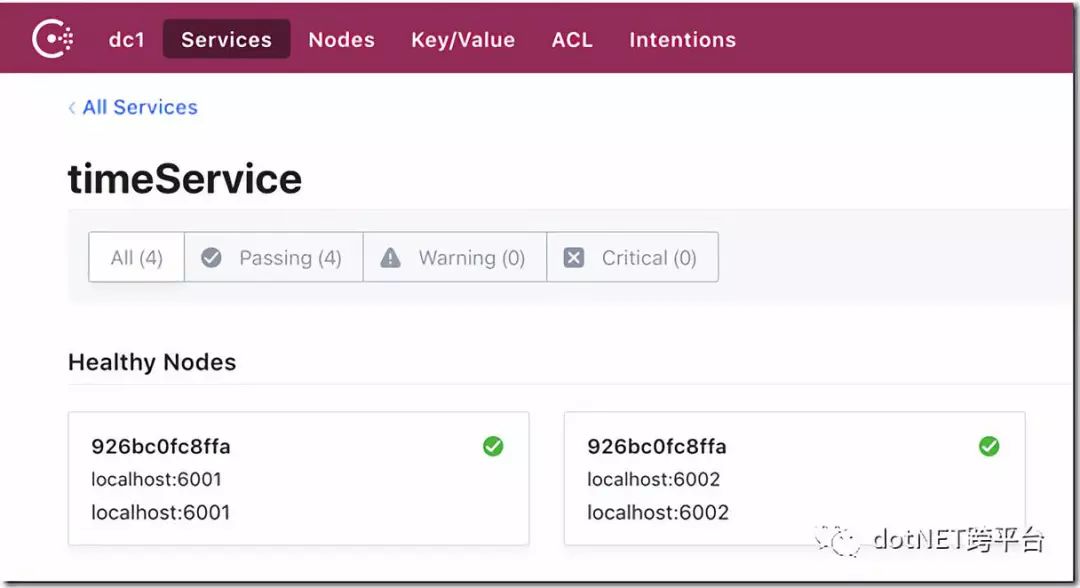
我们可以发现Consul上注册了一个timeService，并且有两个健康的节点，分别是：localhost:6001和localhost:6002。

这样我们就完成了同一个服务两个实例的环境，下一步就是如何调用这些服务。

编写客户端（服务调用方）

配置文件

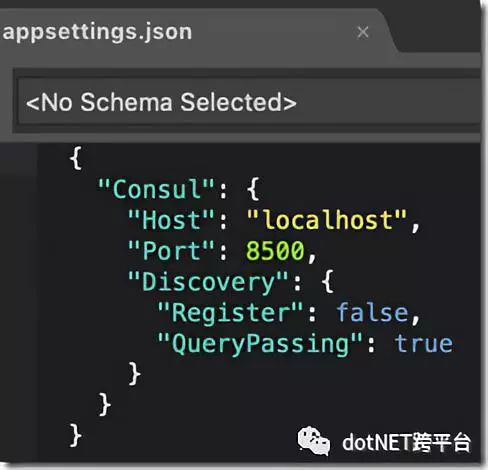
大概的意思是：

配置Consul的地址

当前程序不注册到Consul上（目前只是调用方无需注册到Consul）

只查询健康的服务信息（不健康的节点不会返回）

使用feign调用

定义接口

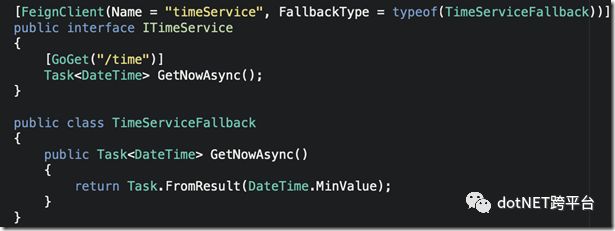
大概的意思是：

定义了一个ITimeService接口，里面有个方法叫GetNowAsync。

在接口定义上添加FeignClientAttribute，指定这个接口对应的服务名称是：timeService（server端的服务名称：Spring:Application:Name），定义一个回退类型（当服务不可用时返回一个可控值，DateTime的最小时间）

初始化和调用

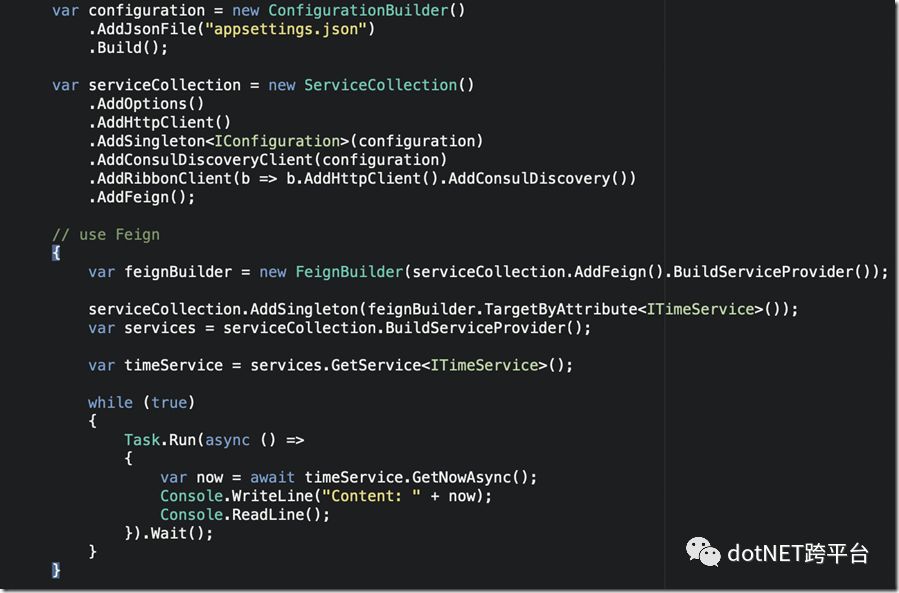
运行

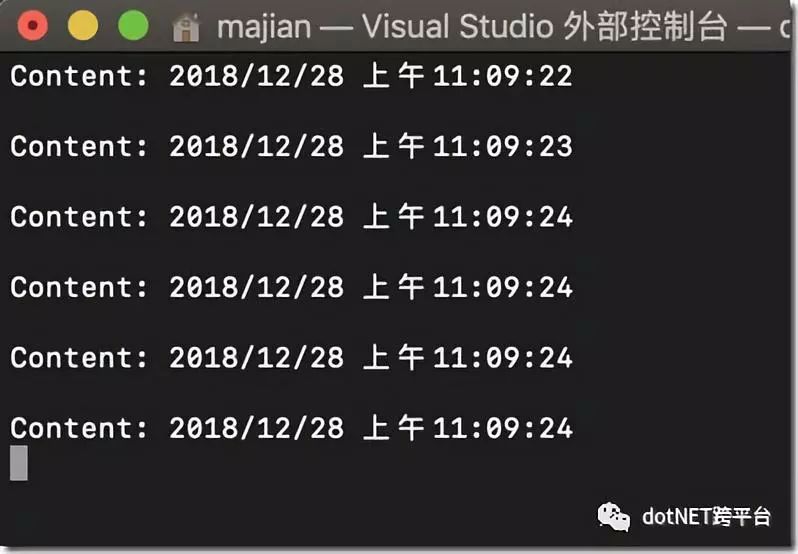
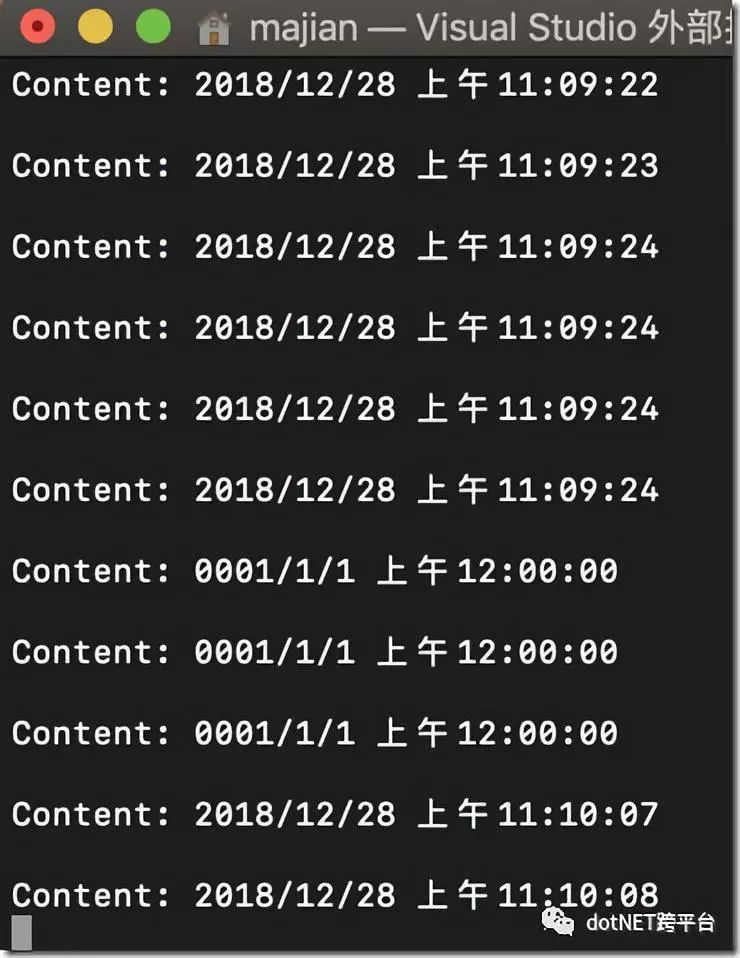
关掉server试试？

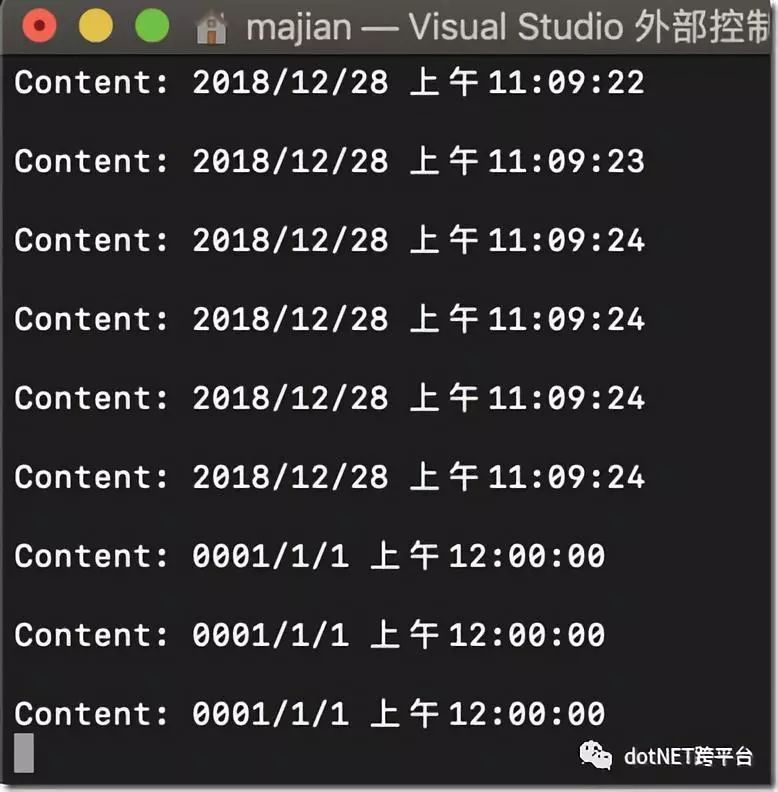
在开启server？

使用HttpClientFactory调用

初始化和调用

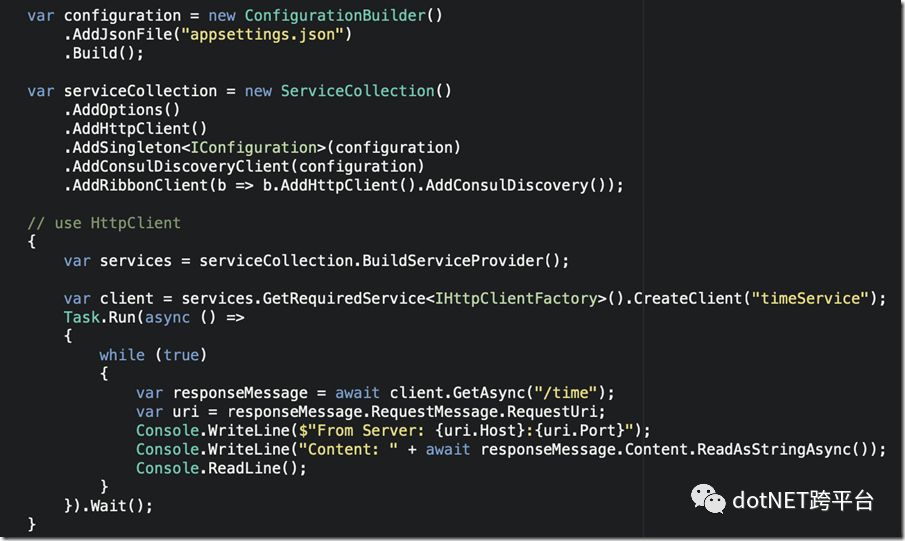
运行

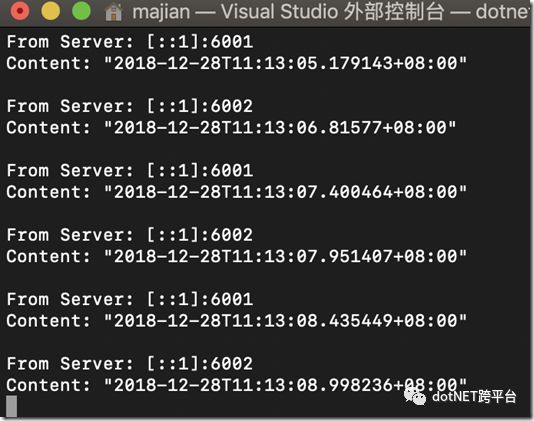
可以看到6001和6002在交替请求，证明采用的策略是轮询。

写在最后

本篇属于开篇，后续会单独介绍ribbon、feign、Steeltoe.Discovery.Consul.Client。

开源的地址如下：

https://github.com/majian159/ribbon

https://github.com/RabbitTeam/steeltoe-extensions

.NET技术栈QQ群：384413261（点击加入 .NET Group）

原文地址: https://www.cnblogs.com/ants/p/10189440.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com