基本概念

无向图：边没有方向(或者称为双向)的图
连通图：如果一个图至少有两个点，那么图任意两个点可以互相到达
子图：如果图G’的点集是图G的点集的子集，且图G’的边集是图G的边集的子集，称G’是G的子图
连通子图：如果G的子图G’是连通图，那么G’就是G的一个连通子图
极大连通子图：如果图G’是G的连通子图，并且不存在图G的另一个连通子图G’‘使得G’是G’‘的子图，称G’为G的极大连通子图，又叫连通分量
极小连通子图：如果图G’是G的连通子图，并且不存在图G的另一个连通子图G’‘使得G’不是G’'的子图，称G’为G的极小连通子图

如果无向图G是连通图，那么G只有一个极大连通子图(连通分量)即它本身，
同时G一定有极小连通子图即它的最小生成树并可能有多个

如果无向图G不是连通图，那么G有多个极大连通子图(连通分量)，
同时G没有极小连通子图。

极大和极小是指集合上的(会不会被其他集合包含)而不是单纯指点或边的数量
好好理解吧实在看不懂其实也无所谓，这种死概念在这里插入图片描述

割点以及点双连通分量

割点：如果去掉无向连通图G中一点x，并去掉所有与x相邻的边，余下的点和边构成的子图G’不再是连通图，那么称x是G的一个割点
点双连通图：如果一个连通图不存在割点，那么可以称之为点双连通图
点双连通分量：如果一个连通分量不存在割点，那么可以称之为点双连通分量
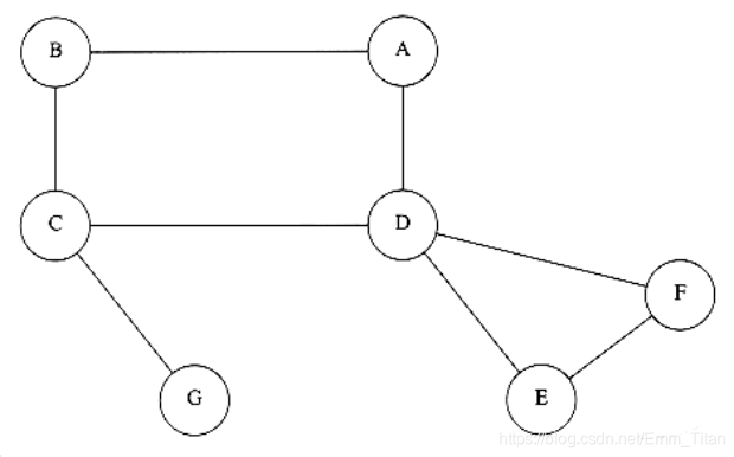
在这里插入图片描述
如图中，c和d就是割点，如果去掉c以及c所对应的所有边，意味着G无法与其他的点联通

A,B,C,D构成了一个点双连通分量;D,E,F也是一个；任意去掉一个点，剩下的点还是连通
C,G并没有构成一个点双连通分量，因为一旦去掉C或者G，就只剩下一个点了，显然并不符合连通图的定义

Tarjan法求割点

推导过程

我们选择图中任意一点u为起点进行dfs，形成一颗搜索树，显然u是搜索树的根
如果x是图的割点，我们考虑x要满足哪些条件：
1.如果x是u，那么x至少有两个子节点
2.如果x不是u，那么x有子节点，
x存在子节点无法在不经过x的情况下到达以x为根的子树外
也就是说至少存在一个点如果要找到一个不属于x的子树的点，必须经过x
那么x就是一个割点，一旦被删掉，那个点无法走到外面的点

解决方案如下：
情况1：我们很容易判断
情况2：我们可以借助tarjan算法中的dfn和low信息来判断
dfn：表示i点在搜索树上的搜索序
low：表示i通过各种边能达到的整棵树深度最小的点

首先我们知道，如果x的某个子节点y能在不经过x的前提下到达以x为根的子树外的点z，那么z的dfn一定小于x
如果low[y]小于dfn[x]，就能说明点y能不通过x到达以x为根的子树外
如果存在任意一个y不满足，就说明x是割点
在这里插入图片描述

代码实现

fa是搜索树上u的父节点，cnt是当前的时间戳，child是搜索树上u的子节点数量，
vec是记录了u邻边的vector，isCut[i]表示i是否是割点。
注意当v是已访问过的点时，是取v的dfn更新u的low

void tarjan ( int u, int fa ) {low[u] = dfn[u] = ++ cnt;int child = 0;for ( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if ( ! dfn[v] ) {child ++;tarjan ( v, u );if ( low[v] >= dfn[u] )//v能走到的深度最小的点都比u大//说明v无法不经过u到达除开u子树外的点isCut[u] = 1;low[u] = min ( low[v], low[u] );//更新能到达的最小的深度的点}else if ( dfn[u] > dfn[v] && v != fa )///v一定不能是u的父亲//v的深度如果比u小，意味着v先被遍历，v就变成了u祖先级别//属于除开u所在子树外的点，证明u可以不经过自己的父亲直接到达vlow[u] = min ( dfn[v], low[u] );}if ( fa < 0 && child == 1 )//这棵树根只有一个儿子 是会被误判成割点的isCut[u] = 0;
}

Tarjan法求点双连通分量

推导过程

根据点双连通分量的定义，我们可以很简单的想到以下方法来求点双连通分量：
1.我们将点按照访问顺序入栈
2.当我们确定x是割点，即x的某个子节点y满足low[y]≥dfn[x]时，
我们将栈中的点依次弹出，直到栈顶为x，
x和我们弹出的这些点构成了一个点双连通分量
注意：x不能弹出，因为x可能属于多个点双连通分量
3.如果x是根，即使不是割点也作如上处理

代码实现

st是按访问顺序储存点的栈，cntd是点双连通分量的数量，vecd[i]是储存第i个点双连通分量里点的vector

void tarjan ( int u, int fa ) {low[u] = dfn[u] = ++ cnt;int child = 0;st.push ( u ); for ( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if ( ! dfn[v] ) {child ++;tarjan ( v, u );if ( low[v] >= dfn[u] ) {isCut[u] = 1;cntd ++;vecd[cntd].push_back ( u );while ( st.top() != u ) {vecd[cntd].push_back ( st.top() );st.pop();}}low[u] = min ( low[v], low[u] );}else if ( dfn[u] > dfn[v] && v != fa )low[u] = min ( dfn[v], low[u] );}if ( fa < 0 && child == 1 ) isCut[u] = 0;if ( fa < 0 && child == 0 ) {//这棵树只有根节点cntd ++;vecd[cntd].push_back ( u );}
}

在这里插入图片描述

有向图的Tarjan缩点

我一般都是这么写的，还挺不错的

void tarjan ( int u ) {dfn[u] = low[u] = ++ cnt;sta.push ( u );for ( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if ( ! dfn[v] ) {tarjan ( v );low[u] = min ( low[u], low[v] );}else if ( ! sccno[v] )low[u] = min ( low[u], dfn[v] );}if ( low[u] == dfn[u] ) {int v;scc ++;do {v = sta.top();sta.pop();sccno[v] = scc;//顺便标记了v属于哪一个强连通分量vecd[scc].push_back( v );}while ( v != u );}
}

桥与边双连通分量

割边：如果去掉无向连通图G中一条边w，余下的点和边构成的子图G’不再是连通图，那么称w是G的一条割边，也成为桥
边双连通图：如果一个连通图不存在桥，那么可以称之为边双连通图
边双连通分量：如果一个连通分量不存在桥，那么可以称之为边双连通分量
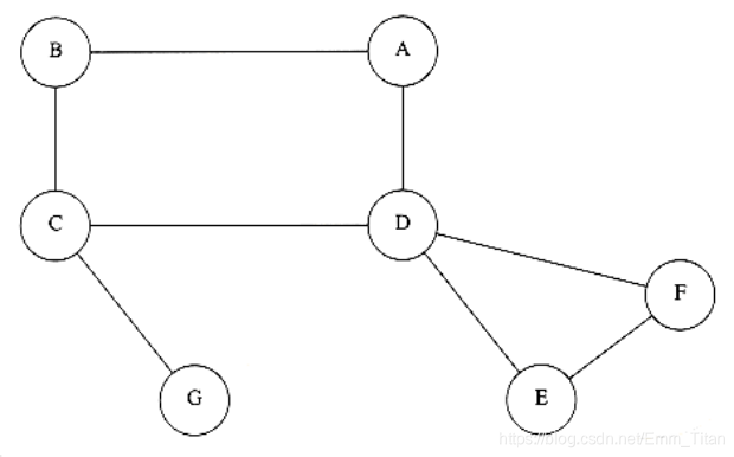
在这里插入图片描述
如图中的CG边就是桥，删掉后G就被孤立了
A,B,C,D,E,F就是一个边双连通分量，任意删掉一条边各个点还是能互相到达

Tarjan法求桥

理论推导

我们选择图中任意一点为起点进行dfs，形成一颗搜索
如果w是图的割边，我们考虑w要满足什么条件：
1.w肯定在搜索树上
2.如果w连接的是x和y，并且在搜索树上x是y的父节点，
那么y无法在不经过w的前提下到达以y为根的子树外
显然，重边是影响桥的判定的。但是重边不影响割点的判定

代码实现

vec是记录了u邻边的vector，to是边的终点，no是边的编号
fano是搜索树上连接u和u父节点的边的编号
isCut[i]表示i是否是桥，注意判断桥的条件和割点有所不同

void tarjan ( int u, int fano ) {low[u] = dfn[u] = ++ cnt;int child = 0;for ( int i = 0;i < vec[u].size();i ++ ) {int v = vec[u][i].to, vno = vec[u][i].no;if ( ! dfn[v] ) {child ++;tarjan ( v, vno );if ( low[v] > dfn[u] )isCut[no] = 1;low[u] = min ( low[v], low[u] );}else if ( dfn[u] > dfn[v] && vno != fano )low[u] = min ( dfn[v], low[u] );}
}

在这里插入图片描述

Upd：重边求桥以及连通块

void dfs1( int u, int lst = -1 ) {
//因为有重边的关系 所以不能用vector 判断是否是父亲的版本
//只能防止反向走同一边的dfn[u] = low[u] = ++ cnt; sta.push( u );for( int i = head[u];~ i;i = E[i].nxt ) {if( i == lst ) continue;int v = E[i].to;if( ! dfn[v] ) {dfs1( v, i ^ 1 );low[u] = min( low[u], low[v] );if( low[v] > dfn[u] ) {tot ++; int now;do {now = sta.top();scc[now] = tot;sta.pop();} while( now ^ v );}}else low[u] = min( low[u], dfn[v] );}
}

Tarjan法求边双连通分量

理论推导

显然，割点是存在于点双连通分量中的并且可能存在于多个点双连通分量中，
因为割点在整张图G里面是割点，但在子图G’里它就可能不再是割点，
上面给的图就是一个栗子。。。。但是桥是不可能存在于边双连通分量中的

所以只需要我们把桥从图中去掉，这样图就变成了多个连通分量，
每个连通分量就是原图的边双连通分量。
然而在实际操作中我们不需要真的去掉桥，过于麻烦，可以考虑只需要将他们标记并且在第二次dfs中不经过他们就行了

代码实现

visit[i]记录了点i是否被访问过
visitno[i]记录了编号为i的边是否被访问过
vecb[i]是记录第i个边双连通分量里边的vector

//此处省略第一次dfs求桥的代码
void dfs ( int u ) {visit[u] = 1;for ( int i = 0;i < vec[u].size();i ++ ) {int v = vec[u][i].to, vno = vec[u][i].no;if ( isCut[vno] == 0 ) {if ( visitno[vno] == 0 ) {visitno[vno] = 1;vecb[cntb].push_back ( vno );}if ( visit[v] == 0 )dfs ( v );}}
}
int main() {for ( int i = 1;i <= n;i ++ )if ( ! visit[i] ) {cntb ++;dfs ( i );}
}