Infinite Tree

题意：

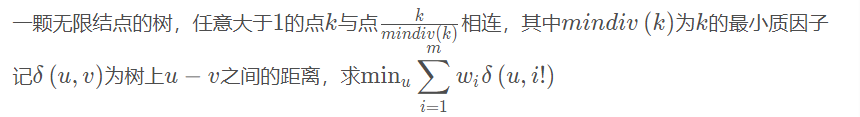
题解：

参考博客
看了好一阵子才明白。。。emm。
我们先按照题意画出一部分树

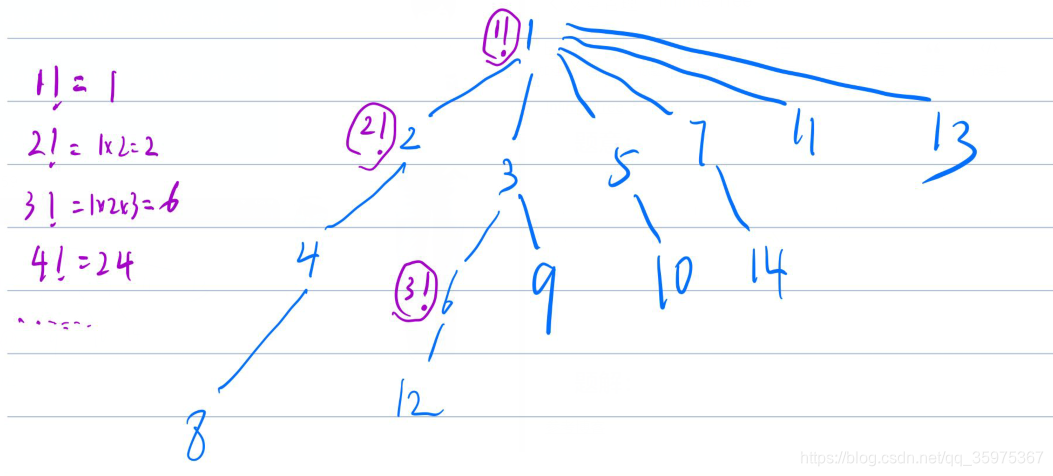
我们先不考虑复杂度，这题应该怎么做？
题目给了每个点的权值w[i]，问一个点到所有的节点路径长度*点权之和最小是多少，很明显是树形dp
dp[i]表示以i为根的子树到i的w和
sum[i]表示乘上距离之后的答案
dep[i]表示深度，now为当前节点，son为子节点
则有：

dp[now]= w[now]
sum[now]=0
dp[now]+=dp[son]
sum[now]+=sum[son]+(dep[son]-dep[now])*sum[son]

但是以now为根并不一定是最佳答案，所以我们还要不断的换根，求出最佳答案
如果将now为根转移到son为根，我们不用重新算一遍，只需要在之前的基础上

sum[now]-=sum[son]+(dep[son]-dep[now])*dp[son]
dp[now]-=dp[son]
sum[son]+=sum[now]+(dep[son]-dep[now])*dp[now]
dp[son]+=dp[now]

这样就OK了
但是！
题目是要求u到i！的距离，i！的增长速度很快，树的增长也是很快，如果全建出来肯定TLE了，所以我们没办法将整棵树建立，只能选择性建立，这要用到虚树
我们将阶乘点当做关键点，保留关键点及其lca，然后建立数就行
现在又有一个新问题，lca怎么计算？
我们首先考虑a！和(a+1)!的dfn谁大？
因为后者的因子一定包含前者的因子，所以除以mindiv后，（a+1）！的深度肯定更大，所以这些阶乘数的dfn是随a值从小到大的，这样我们只需要考虑相邻两个点的lca即可
我们列一个表格记录阶乘数分解后有多少个质数

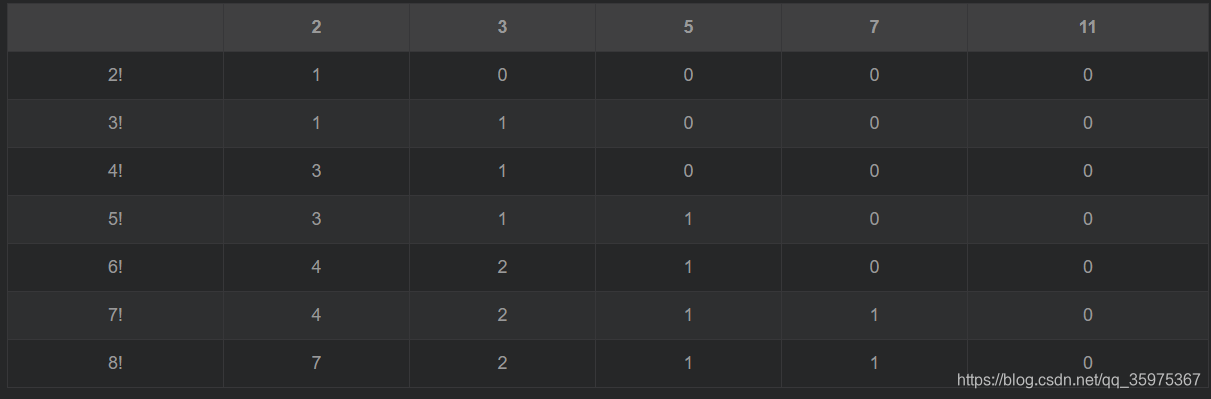
我们根据上面的表格来列出相邻的LCA
2!和3 ! : 1，深度为1
3!和4 ! : 6，深度为3
4!和5 !: 1，深度为1
5!和6 !: 15，深度为3
6!和7 !: 1，深度为1
我们可以得出，对于a！和(a+1)!，LCA就是从大到小公共的质因子的乘积，遇到不同的就停止，深度是相同的个数+1
例如5！和6！：
5！分解后：5 3 2 2 2
6！：5 3 3 2 2 2 2
从大到小，一样的是5和3 ，（从第三位开始不一样，停止）
lca就是15，深度就是3

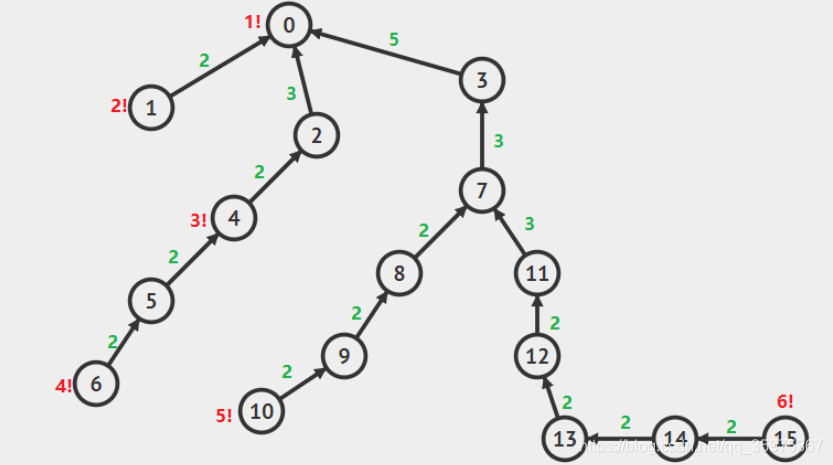
可以得到dep[lca((i+1)!,i!)] = sum(maxdiv(i+1),n)
sum(maxidv(i+1),n)为原本i！中大于等于maxdiv(i+1)的因子个数
这样我们就可以快速算出LCA
但是还是不够快，如果对于每个数都扫一次的话，还是很慢。所以，需要一个快速地查找求和，修改的算法，那就是用到了线段树或树状数组

代码：

#include<bits/stdc++.h>
#define ll long long
#define inf 1ll<<60
using namespace std;
const int MAXN=1e5+10;
int num[MAXN],w[MAXN<<1],d[MAXN<<1],stk[MAXN];
int ldfn[MAXN],rdfn[MAXN],dep[MAXN],lcad[MAXN],m;
int mndv[MAXN],pcnt=0;
ll dp1[MAXN<<1],dp2[MAXN<<1],ans;
vector<int> vir[MAXN<<1];
ll tr[MAXN<<2];//注意开long long
void Build(int root,int l,int r)
{tr[root]=0;if(l==r) return;int mid=l+r>>1;Build(root<<1,l,mid);Build(root<<1|1,mid+1,r);
}
void Change(int root,int l,int r,int x)
{if(l==r){tr[root]++;return;}int mid=l+r>>1;if(x<=mid) Change(root<<1,l,mid,x);else Change(root<<1|1,mid+1,r,x);tr[root]=tr[root<<1]+tr[root<<1|1];
}//x是插入的质数，要将其计数+1
int Query(int root,int x,int l,int r)
{              if(l>=x) return tr[root];int mid=l+r>>1;if(x<=mid) return Query(root<<1,x,l,mid)+Query(root<<1|1,x,mid+1,r);else if(x>mid) return Query(root<<1|1,x,mid+1,r);
}//查找当前质数的个数
void build()
{//^不等于，相当于!=dep[1]=1;for(int i=2;i<=m;i++){dep[i]=dep[i-1];int j=i;while(j^mndv[j]) j/=mndv[j];lcad[i]=Query(1,j,1,m)+1;for(j=i;j^1;dep[i]++,j/=mndv[j]) Change(1,1,m,mndv[j]);}int top=0,tot=m;stk[++top]=1;for(int i=2;i<=m;i++){if(top==1||lcad[i]==dep[stk[top]]){stk[++top]=i;continue;}while(top>1&&lcad[i]<=dep[stk[top-1]]){vir[stk[top-1]].push_back(stk[top]);top--;}//建虚树的基本操作，不会的建议去学习一下if(lcad[i]^dep[stk[top]]){dep[++tot]=lcad[i];w[tot]=0;vir[tot].push_back(stk[top]);stk[top]=tot;}stk[++top]=i;}while(top>1){vir[stk[top-1]].push_back(stk[top]);top--;}
}//原理同上，供参考
void dfs1(int x,int fa)
{dp1[x]=w[x];dp2[x]=0;for(int i=0;i<vir[x].size();i++){int son=vir[x][i];if(son==fa) continue;dfs1(son,x);dp1[x]+=dp1[son];dp2[x]+=dp2[son]+(dep[son]-dep[x])*dp1[son];}
}
void dfs2(int x,int fa)
{ans=min(ans,dp2[x]);for(int i=0;i<vir[x].size();i++){int son=vir[x][i];if(son==fa) continue;ll x1=dp1[x],x2=dp2[x],son1=dp1[son],son2=dp2[son];dp2[x]-=dp2[son]+(dep[son]-dep[x])*dp1[son];dp1[x]-=dp1[son];dp2[son]+=dp2[x]+(dep[son]-dep[x])*dp1[x];dp1[son]+=dp1[x];dfs2(son,x);dp1[x]=x1,dp2[x]=x2,dp1[son]=son1,dp2[son]=son2;}
}//树形dp+换根，非重点，且是模板一套的问题，上面已经分析
int main()
{mndv[1]=1;for(int i=2;i<MAXN;i++)if(!mndv[i])for(int j=i;j<MAXN;j+=i)if(!mndv[j]) mndv[j]=i;//预处理出每个数的mindiv，之后分解时可以用while(~scanf("%d",&m)){for(int i=1;i<=m;i++)scanf("%d",&w[i]);for(int i=0;i<=m*2;i++){vir[i].clear();dp1[i]=dp2[i]=0;}Build(1,1,m);build();dfs1(1,0);ans=dp2[1];dfs2(1,0);printf("%lld\n",ans);}
}

#include<bits/stdc++.h>
#define lowbit(x) x&-x
using namespace std;
typedef long long ll;
const int MAX = 2e5 + 10;
//建立虚树点数tot < 2n, 空间开两倍int n, w[MAX];
ll ans;//树状数组
int c[MAX];
void upd(int p, int k) { for (; p <= n; p += lowbit(p)) c[p] += k; }
int query(int p) { int res = 0; for (; p; p -= lowbit(p)) res += c[p]; return res; }int mindiv[MAX];
void sieve(int siz) {//筛mindivfor (int i = 2; i <= siz; i++)if (!mindiv[i])for (int j = i; j <= siz; j += i)if (!mindiv[j])mindiv[j] = i;
}int lcadep[MAX], dep[MAX];
int st[MAX], top, tot;//stack, top, tot:虚树点数
vector<int> g[MAX];//虚树
void add_edge(int u, int v) { g[u].push_back(v), g[v].push_back(u); }void buildVirtualTree() {tot = n;st[top = 1] = 1;for (int i = 2; i <= n; i++) {dep[i] = dep[i - 1] + 1; int j = i;for (; j != mindiv[j]; j /= mindiv[j]) dep[i]++;lcadep[i] = query(n) - query(j - 1);for (j = i; j != 1; j /= mindiv[j]) upd(mindiv[j], 1);}//建树for (int i = 2; i <= n; i++) {while (top > 1 && dep[st[top - 1]] >= lcadep[i])add_edge(st[top - 1], st[top]), top--;if (dep[st[top]] != lcadep[i]) {dep[++tot] = lcadep[i];add_edge(tot, st[top]);st[top] = tot;}st[++top] = i;}while (top > 1){add_edge(st[top - 1], st[top]);top--;}
}void dfs(int u, int fa) {ans += 1ll * w[u] * dep[u];//ans最开始是rt = 1时的答案for (auto &v: g[u])if (v != fa) {dfs(v, u);w[u] += w[v];}
}void dfs2(int u, int fa) {//如果rt移动之后答案变小就一直移动下去，直到答案不在变小for (auto &v: g[u])if (v != fa) {//rt从u转移到v的代价//+(w[1] - w[v]) - w[v]if (w[1] - 2 * w[v] < 0) {ans += 1ll * (w[1] - 2 * w[v]) * (dep[v] - dep[u]);//一步的代价*距离dfs2(v, u);}}
}void init() {ans = top = 0;for (int i = 1; i <= tot; i++) {g[i].clear();c[i] = w[i] = lcadep[i] = dep[i] = 0;}
}int main() {sieve(1e5);while (~scanf("%d", &n)) {init();for (int i = 1; i <= n; i++) scanf("%d", &w[i]);buildVirtualTree();int rt = 1;dfs(rt, 0);dfs2(rt, 0);printf("%lld\n", ans);}return 0;
}