【做题记录】CodeForces 做题记录

链接放的是洛谷上的链接，难度就是 CF 上的评分。

<details><summary>$\texttt{solution}$</summary></details>

CF10D LCIS

难度：\(\tt{2800}\)

求两个串的最长公共上升子序列。\(n\le 500\)

$\texttt{solution}$

严重虚高题，但我是个 saber

求两个串的最长公共子序列，设 \(f_{i,j}\) 表示到 \(s_i,t_j\) 的最大匹配。

求一个串的最长上升子序列，记下最大值为 \(i\) 时的答案。

那么。。合并！！！

设 \(f_{i,j}\) 表示当前以 \(s_i\) 这个数结尾，到 \(t\) 串第 \(j\) 个位置的最大匹配。

则每次转移可以从 \(k\le i,p<j\) 处转移而来,二维树状数组即可。

CF1579G Minimal Coverage

难度：\(\texttt{2200}\)

给你 \(n\) 条线段，告诉你每条线段的长度。

你需要把它们放在一条无限长的数轴上。放置需满足当前线段的起点是前一个线段的终点，特别的第一个线段的起点为 \(0\)。

也就是说，若前一个线段的终点是 \(x\)，当前长度为 \(d\)，那么这个线段必须放在 \([x-d,x]\) 终点变为 \(x-d\)，或 \([x, x + d]\) 终点变为 \(x + d\)。

请问放置完后所有线段的最小覆盖长度是多少？

\(1\le t\le 10^4, 1\le n\le 10^4\)

$\texttt{solution}$

第一遍没有做出来的原因只要是主要不知道怎样规定 dp 状态。

考虑设 \(dp(i,j)\) 表示第 \(i\) 条边，当前端点距离左端点为 \(j\) 时的最短扩展距离。

之后转移就变得方便多了。

CF1575L Longest Array Deconstruction

难度：\(\texttt{2100}\)

设 \(a\) 是一个序列，定义 \(f_a\) 表示满足 \(a_i=i\) 的位置 \(i\) 的数目。

给你一个长度为 \(n\) 的序列 \(a\)，可以删除若干个数字，最大化 \(f_a\)。

\(1\le n,a_i\le 2\times 10^5\)

$\texttt{solution}$

\(\texttt{solution1:}\)

我们考虑朴素的 \(n^2\) dp 怎么做：

咕咕咕

\(\texttt{solution2:}\)

我们考虑一个数如果要被选择它必须向左移动 \(i-a_i\) 个位置(如果 \(i-a_i<0\) 那么它必然不会被选择)。

如果我们要选择一串位置，那么必须保证他们的 \(i-a_i\) 不下降(当然同时要保证 \(a_i\) 递增)。

这样容易想到 \(\text{LIS}\) 问题，即单调上升(不下降)子序列问题，直接套板子求解即可。

#define Maxn 200005
int n,ans,minn[Maxn];
pa a[Maxn];
int main()
{n=rd();for(int i=1;i<=n;i++) a[i]=pa(rd(),-i);sort(a+1,a+n+1);for(int i=1,pos,x;i<=n;i++){x=-a[i].se-a[i].fi;if(x<0) continue;pos=upper_bound(minn+1,minn+ans+1,x)-minn;minn[pos]=x,ans=max(ans,pos);}printf("%d\n",ans);return 0;
}

CF1582F2 Korney Korneevich and XOR (hard version)

难度：\(\texttt{2400}\)

给一个长度为 \(n\) 的序列 \(a_1,a_2,\dots,a_n\)。

要求选出一段子序列 \(a_{p_1},a_{p_2},\dots,a_{p_k}\) 满足 \(p_1<p_2<\dots<p_k\) 且 \(a_{p_1}<a_{p_2}<\dots<a_{p_k}\)，设这段子序列中每个元素的异或之和为 \(t\)，求出 \(a\) 的所有子序列可能存在的异或和并自小而大输出。

\(n\le 10^6,max{a}\le 5000\)

$\texttt{solution}$

我们考虑到以一个数为结尾的子序列中可能出现的异或和个数不超过 \(8291=2^{13}-1\)，所以我们需要对于一个数以及以前的异或和加以讨论。

我们有注意到如果对于 \(i<j,a_i=a_j\) 以它们为结尾的子序列为相同的异或和，那么我们完全可以只考虑 \(i\) 而忽略 \(j\)。

因此我们对于同一个数结尾，最多有 \(2^{13}\) 可能的异或，只要我们只处理这些数复杂度就是对的了。

对于一个已知的异或和，我们可以枚举比 \(a_i\) 大的所有数并给它们记录这个异或和(注意如果发现有一个数记录过这个异或和那么不用再往下拉，因为它后面的位置都由上一次记录这个数的时候记录过了)。

最后统计答案即可。

这一题发现 \(n\) 的复杂度必须是线性的，而值域为 \(5000\)，引导我们向 \(val^2\) 的方向思考。

要多考虑正解复杂度与优化。

#define Maxn 1000005
#define Maxa 8200
int n,All=8191;
int a[Maxn];
bitset<Maxa> ans[Maxa],vis[Maxa];
vector<int> pre[Maxn];
int main()
{n=rd();for(int i=0;i<=All;i++) pre[i].pb(0);for(int i=1;i<=n;i++){a[i]=rd();if(!vis[a[i]][a[i]]) pre[a[i]].pb(a[i]),vis[a[i]][a[i]]=true;}for(int i=1;i<=n;i++){for(int j:pre[a[i]]){ans[a[i]][j]=true;for(int k=a[i]+1;k<=5000;k++){if(vis[k][k^j]) break;vis[k][k^j]=true,pre[k].pb(k^j);}}pre[a[i]].clear();}for(int i=1;i<=5000;i++) ans[0]|=ans[i];printf("%lld\n",ans[0].count());for(int i=0;i<=All;i++) if(ans[0][i]) printf("%d ",i);printf("\n");return 0;
}

CF1601C Optimal Insertion

难度：\(\texttt{2300}\)

给定两个序列 \(a,b\)，长度分别为 \(n,m(1\leq n,m\leq 10^6)\)。接下来将 \(b\) 中的所有元素以任意方式插入序列 \(a\) 中任意位置，请找出一种插入方式使结果序列中的逆序对数量最小化，并输出这个最小值。

关于插入：任意方式插入任意位置的示例如下。

例如 \(a=\{1,2,3,4\},b=\{4,5,6\}\)，则 \(c=\{4,\underline1,5,\underline2,\underline3,\underline4,6\},\{\underline1,\underline2,6,5,\underline3,4,\underline4\}\dots\) 均为合法的插入方式。但你不能修改 \(a\) 的顺序。

$\texttt{solution}$

首先有一个结论：如果把 \(b\) 排序后加入答案一定不变劣。

如果 \(b\) 没排好序，交换 \(b\) 的两个逆序元素答案不会变劣。

之后考虑分治的方法求解，我们先将 \(b[mid]\) 加入最佳位置中，再分左右加入左边与右边(这样可以减小复杂度，不用每个数去求最小值)。

可以设 \(pos(i)\) 表示将 \(b_i\) 加入 \(a_{pos(i)}\) 以前(特别的，如果加载序列末尾，\(pos=n+1\))。

最后用树状数组求解最终逆序对即可。

#define Maxn 2000005
int n,m,cnt,tot;
int in_tr[Maxn],a[Maxn],b[Maxn],seq[Maxn],pos[Maxn],L[Maxn],R[Maxn];
ll ans;
map<int,int> tr_in;
struct BIT
{int tree[Maxn];inline void init(){ for(int i=1;i<=cnt;i++) tree[i]=0; }inline void add(int x,int k){ while(x<=cnt) tree[x]+=k,x+=x&(-x); }inline int query(int x){ int ret=0; while(x) ret+=tree[x],x-=x&(-x); return ret; }
};
BIT T;
void solve(int l,int r,int nl,int nr)
{if(nl>nr) return;int mid=(nl+nr)>>1,cho=0,minn=inf;L[l]=R[r]=0;for(int i=l+1;i<=r;i++) L[i]=L[i-1]+(a[i-1]>b[mid]);for(int i=r-1;i>=l;i--) R[i]=R[i+1]+(b[mid]>a[i]);for(int i=l;i<=r;i++) if(L[i]+R[i]<minn) minn=L[i]+R[i],cho=i;pos[mid]=cho;solve(l,cho,nl,mid-1),solve(cho,r,mid+1,nr);
}
bool cmp(int x,int y){ return x<y; }
int main()
{int Test=rd();while(Test--){n=rd(),m=rd(),cnt=tot=ans=0;for(int i=1;i<=n;i++) a[i]=rd(),in_tr[++cnt]=a[i];for(int i=1;i<=m;i++) b[i]=rd(),in_tr[++cnt]=b[i];sort(in_tr+1,in_tr+cnt+1,cmp),sort(b+1,b+m+1,cmp);cnt=unique(in_tr+1,in_tr+cnt+1)-in_tr-1;for(int i=1;i<=cnt;i++) tr_in[in_tr[i]]=i;for(int i=1;i<=n;i++) a[i]=tr_in[a[i]];for(int i=1;i<=m;i++) b[i]=tr_in[b[i]];solve(1,n+1,1,m);for(int r=1,l=1;r<=m;r++){while(l<=n && l<pos[r]) seq[++tot]=a[l],l++;seq[++tot]=b[r];}for(int i=pos[m];i<=n;i++) seq[++tot]=a[i];for(int i=1;i<=tot;i++) ans+=1ll*(i-T.query(seq[i])-1),T.add(seq[i],1);printf("%lld\n",ans);T.init();}return 0;
}

CF1557D Ezzat and Grid

难度：\(\texttt{2200}\)

有一个 \(n\) 行 \(10^9\) 列的表格。

Diana 会执行 \(m\) 次操作，每次操作会将第 \(i\) 行的第 \([l,r]\) 格涂黑。

Diana 想知道，至少删掉几行后，对于每相邻的两行，都存在至少一列，使得这两行的这一列都涂黑了。

\(n,m\le 3\times 10^5\)，一个格子可能被涂黑多次。

$\texttt{solution}$

一道恶心 DS 题，主要是码量大，难调 /tuu

先考虑容斥(正难则反)，用总方案数减去最多能够保存的行数。

我们现将坐标离散化，考虑用线段树维护当前，每个横坐标对应的列为黑(即如果需要匹配的行这一列也为黑，可以由这一列匹配过来)时最大的保存行数。

这样每次更新行的时候直接取区间最大值，转移到当前行最大值即可。

值得注意的是，题目描述中特意说明了可能会有区间包含或重叠的情况，那么我们在更新一个节点时不仅要判断这个节点的最大值是否需要更新，也要判断懒惰标记是否也能够更新。因为有从儿子继承最大值时不能继承懒惰标记，而是这时可以更新子树内的最大值而不能更新这个节点最大值。

#define Maxn 600005
typedef long long ll;
int n,m,cnt,l,r,x,P,ans;
int in_tr[Maxn],pos[Maxn],L[Maxn],R[Maxn];
bool exist[Maxn];
struct TREE
{int laz,maxx,num;inline void to_max(int tmpl,int tmpn) { if(tmpl>=maxx) maxx=laz=tmpl,num=tmpn; }inline void init() { laz=maxx=num=0; }
};
TREE tree[Maxn<<2],dp[Maxn];
vector<pa> hav[Maxn];
map<int,int> tr_in;
inline void pushdown(int p)
{tree[p<<1].to_max(tree[p].laz,tree[p].num);tree[p<<1|1].to_max(tree[p].laz,tree[p].num);
}
inline TREE merge(TREE pl,TREE pr)
{TREE ret; ret.init();if(pl.maxx<pr.maxx) ret.maxx=pr.maxx,ret.num=pr.num;else ret.maxx=pl.maxx,ret.num=pl.num;return ret;
}
void change(int p,int nl,int nr)
{if(nl>=l && nr<=r) { tree[p].to_max(x,P); return; }pushdown(p);int mid=(nl+nr)>>1;if(mid>=l) change(p<<1,nl,mid);if(mid<r) change(p<<1|1,mid+1,nr);tree[p]=merge(tree[p<<1],tree[p<<1|1]);
}
TREE query(int p,int nl,int nr)
{if(nl>=l && nr<=r) return tree[p];pushdown(p);int mid=(nl+nr)>>1; TREE ret; ret.init();if(mid>=l) ret=merge(ret,query(p<<1,nl,mid));if(mid<r) ret=merge(ret,query(p<<1|1,mid+1,nr));tree[p]=merge(tree[p<<1],tree[p<<1|1]);return ret;
}
inline void Change(int tmpl,int tmpr,int tmpx,int tmpp)
{ l=tmpl,r=tmpr,x=tmpx,P=tmpp,change(1,1,cnt); }
inline TREE Query(int tmpl,int tmpr) { l=tmpl,r=tmpr; return query(1,1,cnt); }
bool cmp(int x,int y){ return x<y; }
int main()
{n=rd(),m=rd();for(int i=1;i<=m;i++){pos[i]=rd(),L[i]=rd(),R[i]=rd(),in_tr[++cnt]=L[i],in_tr[++cnt]=R[i];if(L[i]>R[i]) swap(L[i],R[i]);}sort(in_tr+1,in_tr+cnt+1,cmp);cnt=unique(in_tr+1,in_tr+cnt+1)-in_tr-1;for(int i=1;i<=cnt;i++) tr_in[in_tr[i]]=i;for(int i=1;i<=m;i++) hav[pos[i]].pb(pa(tr_in[L[i]],tr_in[R[i]]));for(int i=1;i<=n;i++){for(pa j:hav[i]) dp[i]=merge(dp[i],Query(j.fi,j.se));dp[i].maxx++;for(pa j:hav[i]) Change(j.fi,j.se,dp[i].maxx,i);}for(int i=1;i<=n;i++) if(dp[i].maxx>=dp[ans].maxx) ans=i;printf("%d\n",n-dp[ans].maxx);for(int tmp=ans;tmp;tmp=dp[tmp].num) exist[tmp]=true;for(int i=1;i<=n;i++) if(!exist[i]) printf("%d ",i);if(n-dp[ans].maxx) printf("\n");return 0;
}

CF1556F Sports Betting

难度：\(\texttt{2500}\)

有 \(n\ (n\le14)\) 个人，两两之间会打比赛。每人有一个实力值 \(a_i\)，在 \(i\) 与 \(j\) 的比赛中，\(i\) 有 \(\frac {a_i}{a_i+a_j}\) 的概率获胜，其他情况则是 \(j\) 获胜。\(i\) 在与 \(j\) 的比赛中获胜则称 \(i\) 打败了 \(j\)。若 \(i\) 打败了 \(j\)，\(j\) 打败了 \(k\)，则认为 \(i\) 也打败了 \(k\)。若 \(i\) 打败了除了他自己以外的所有人，则称 \(i\) 是一个 Winner(是否打败了自己不要求)，注意 Winner 可能有多个。现在你需要求出 Winner 的期望数量，对 \(1e9+7\) 取模。

$\texttt{solution}$

首先想到 dp，设 \(f(i,S)\) 表示在 \(S\) 集合中 \(i\) 直接或间接打败了所有人的概率，那么答案为 \(\sum_{i=1}^{n} f(i,2^n-1)\)。

如果要顺序推 dp(也可以成为刷表)，也就是考虑一个一个将元素加入 \(S\) 中，会出现重复计算的情况：先加入 \(a\) 再加入 \(b\) 和先加入 \(b\) 再加入 \(a\) 是同一个东西。

那么考虑填表，也就是用其他值直接计算出这个状态的值。

由于计算 \(i\) 赢了其他人较为困难，将计算倒过来，计算 \(i\) 没有赢其他所有人的概率。

那么可以得出这样的式子：

\(f(i,S)=1-\sum_{i\in T,T\varsubsetneq S}f(i,T)\times g(T,S-T)\)

其中 \(g(A,B)\) 表对于 \(\forall i\in A,j\in B\)，都有 \(j\) 赢了 \(i\) 的概率。

之后就可以直接转移啦。

$\texttt{code}$

#define Maxn 15
#define Maxpown 32800
#define mod 1000000007
typedef long long ll;
int n,All;
ll ans,a[Maxn],inv[Maxn][Maxn];
ll f[Maxn][Maxpown],h[Maxn][Maxpown];
inline ll ksm(ll x,int y)
{int ret=1;for(;y;y>>=1,x=1ll*x*x%mod) if(y&1) ret=1ll*ret*x%mod;return ret;
}
inline void pre_work()
{// h[i][s] : i is beaten by all contants of s// 为了快速算出后面的 gfor(int i=1;i<=n;i++)for(int s=0;s<=All;s++) if(!(s & (1<<(i-1)))){h[i][s]=1;for(int j=1;j<=n;j++) if(s & (1<<(j-1)))h[i][s]=h[i][s]*a[j]%mod*inv[i][j]%mod;}
}
inline void solve(int x)
{for(int s=0,g;s<=All;s++) if(s & (1<<(x-1))){for(int t=(s-1)&s;t;t=(t-1)&s) if(t & (1<<(x-1))){g=1;for(int i=1;i<=n;i++) if(t & (1<<(i-1)))g=g*h[i][s^t]%mod;f[x][s]=(f[x][s]+f[x][t]*g%mod)%mod;}f[x][s]=(1-f[x][s]+mod)%mod;}
}
int main()
{n=rd(),All=(1<<n)-1;for(int i=1;i<=n;i++) a[i]=rd();for(int i=1;i<n;i++) for(int j=i+1;j<=n;j++)inv[i][j]=inv[j][i]=ksm(a[i]+a[j],mod-2);pre_work();for(int i=1;i<=n;i++) solve(i),ans=(ans+f[i][All])%mod;printf("%lld\n",ans);return 0;
}

CF1554E You

难度：\(\texttt{2600}\)

给你一个 \(n\) 个点的树，可以通过以下方式生成一个长度为 \(n\) 的序列 \(a\)：

每次在树中选取一个未被标记的节点 \(u\)，令 \(a_u\) 等于与节点 \(u\) 相邻的未被标记的节点个数，然后将节点 \(u\) 标记。

对于每一个整数 \(k\in[1,n]\)，输出符合以下条件的序列 \(a\) 的数量模 \(998244353\) 的值：

• 序列 \(a\) 可以由给定的树通过上述方式生成。
• \(\gcd(a_1,a_2,\cdots,a_n)=k\)。

\(n\le 10^6\)

$\texttt{solution}$

想一想，如果 \(k\) 给定，我们会怎么做？

可以用一遍 dfs，判断这个点是否需要删除或即将被删除，如果可以删除就直接删除。判断代码如下：

$\texttt{code}$

int dfs(int x,int fa)
{int tmp=ind[x];for(int i=hea[x];i;i=nex[i]){if(ver[i]==fa) continue;tmp-=dfs(ver[i],x);}if(tmp!=Now && (tmp-1)!=Now) exist=0;if(tmp==Now) return 1;else return 0;
}

显然对于每一个 \(k(2\le k\le n)\) 都去判断过去是多余的，因为这是一棵树，而删除后 \(\sum a_i=n-1\)，所以只用枚举 \(n-1\) 的因子就够了。

\(ans_i\) 为 \(2^{n-1}-\sum ans_i\)。

那么由上我们足以通过赛时的数据啦。

如果还要优化，因为 \(n\le 10^6\) 不能放这个 \(n\sqrt{n}\) 的算法通过。

结论 \(1\)：对于 \(k>1,ans_k\in{0,1}\)。

这个比较显然，因为我们在判断中能给每一条边定向，因此删一个去所有点的方案一定，答案只能为 \(0\) 或 \(1\)。

结论 \(2\)：对于 \(n\) 的每一个质因子 \(d\)，没有或仅有一个 \(p(d|p)\)，使得 \(ans_p=1\)。

考虑给一条边定向：设子树可用的大小为 \(k\)。如果 \(d|k\)，那么这条边是从下到上，先删儿子再删根；如果 \(d|(k-1)\)，那么一定是先删父亲再删儿子。

由于我们只考虑质数，所以每当我们要判断一条边的方向时，我们一定能够唯一求出这条边的方向(不可能同时满足以上两种条件)。

因此再素数相同时，这棵树每一条边的方向都将被确定，只有一个素数满足条件。

$\texttt{code}$

#define Maxn 3000005
#define mod 998244353
typedef long long ll;
inline int gcd(int x,int y){ return (y==0)?x:gcd(y,x%y); }
int n,tot,k,Now,exist,pos;
int hea[Maxn],nex[Maxn<<1],ver[Maxn<<1];
int ans[Maxn],ind[Maxn];
inline void add(int x,int y){ ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot; }
int dfs(int x,int fa)
{int tmp=ind[x];for(int i=hea[x];i;i=nex[i]){if(ver[i]==fa) continue;tmp-=dfs(ver[i],x);}if(tmp%Now && (tmp-1)%Now) exist=0;if(tmp%Now==0) { pos=gcd(pos,tmp); return 1; }else { pos=gcd(pos,tmp-1); return 0; }
}
int main()
{int T=rd();while(T--){n=rd(),tot=0;for(int i=1;i<=n;i++) hea[i]=ans[i]=ind[i]=0;for(int i=1,x,y;i<n;i++)x=rd(),y=rd(),add(x,y),add(y,x),ind[x]++,ind[y]++;ans[1]=1;for(int i=1;i<n;i++) ans[1]=ans[1]*2%mod;for(int i=2,tmp=n-1;i<=tmp;i++) if(tmp%i==0){pos=0,Now=i,exist=1,dfs(1,0);if(exist) ans[pos]=exist;while(tmp%i==0) tmp/=i;}for(int i=2;i<=n;i++) ans[1]=(ans[1]-ans[i]+mod)%mod;for(int i=1;i<=n;i++) printf("%d ",ans[i]);printf("\n");}return 0;
}

CF1263F Economic Difficulties

难度：\(\texttt{2400}\)

给你两棵树，结点分别是 \(1,\dots A\) 与 \(1,\dots B\)，然后给了 \(N\) 台设备，并且 \(A\) 树和 \(B\) 树的叶子结点(两棵树的叶子节点数量相同)都是链接电机的。

求最多可以删掉几条边，使得每个电机都能连到任意一棵(或两棵)树的根节点(\(1\) 号点)。

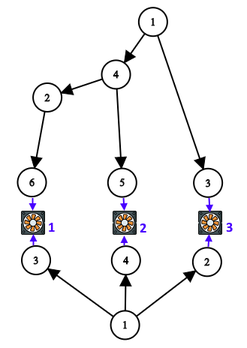
$\texttt{solution}$

我们发现题目中似乎让我们求一个“最大割”，而显然我们需要寻找一个“最小割”模型。

发现如果我们删去一些树边，那么一定会删除这条树边以及一整条路径。

那么我们考虑从一棵树出发向另一棵树流最大流。

注意到我们要保证所有电机都被接通，所以是最大流。

我们从源点向第一棵树除了 \(1\) 号点外每一个节点连流量为 \(1\) 的边，从第二棵树除了 \(1\) 号点的所有点向汇点连流量为 \(1\) 的边。

在树上的边中互相连流量为 \(\infty\) 的边，保证不被删掉。

之后直接跑最小割板子就行啦。

$\texttt{code}$

#define Maxn 5005
#define Maxm 50005
typedef long long ll;
struct ISAP
{#define Maxn 5005#define Maxm 50005int _n,tot=1,_s,_t,All;int dep[Maxn],cnt[Maxn];int tmphea[Maxn],hea[Maxn],nex[Maxm<<1],ver[Maxm<<1];ll sum,edg[Maxm<<1];inline void init(int n,int s,int t){// tot=1; 看情况决定是否要加 All=_n=n,_s=s,_t=t,dep[s]=dep[t]=cnt[n+1]=cnt[n+2]=0;for(int i=1;i<=n;i++) dep[i]=0,cnt[i]=0;}inline void add_edge(int x,int y,ll d){ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot,edg[tot]=d;ver[++tot]=x,nex[tot]=hea[y],hea[y]=tot,edg[tot]=0;}void bfs(){queue<int> q; q.push(_t),dep[_t]=1;while(!q.empty()){int cur=q.front(); q.pop();for(int i=hea[cur];i;i=nex[i]) if(!dep[ver[i]])dep[ver[i]]=dep[cur]+1,q.push(ver[i]);}for(int i=1;i<=_n;i++) cnt[dep[i]]++;if(_s>_n) cnt[dep[_s]]++,All++;if(_t>_n) cnt[dep[_t]]++,All++;}ll dfs(int x,ll flow){if(x==_t) return flow;ll used=0;for(int i=tmphea[x],tmp;i;i=nex[i]){tmphea[x]=i;if(edg[i]>0 && dep[ver[i]]==dep[x]-1){if((tmp = dfs(ver[i],min(flow-used,edg[i]))) > 0)edg[i]-=tmp,edg[i^1]+=tmp,used+=tmp;if(used==flow) return flow;}}if(!(--cnt[dep[x]])) dep[_s]=All+1;cnt[++dep[x]]++; return used;}inline ll solve(){bfs(),sum=0;while(dep[_s]<=All) memcpy(tmphea,hea,sizeof(hea)),sum+=dfs(_s,infll);return sum;}
//	 #undef Maxn
//	 #undef Maxm
}G;
int n,a,b;
int l[Maxn],r[Maxn];
int main()
{n=rd();a=rd();for(int i=2,x;i<=a;i++) x=rd(),G.add_edge(x,i,inf);for(int i=1;i<=n;i++) l[i]=rd();for(int i=2;i<=a;i++) G.add_edge(5001,i,1);b=rd();for(int i=2,x;i<=b;i++) x=rd(),G.add_edge(i+a,x+a,inf);for(int i=1;i<=n;i++) r[i]=rd();for(int i=2;i<=b;i++) G.add_edge(i+a,5002,1);for(int i=1;i<=n;i++) G.add_edge(l[i],r[i]+a,inf);G.init(a+b,5001,5002);printf("%lld\n",a+b-2-G.solve());return 0;
}

CF348D Turtles

难度：\(\texttt{2500}\)(经典题 dp + 容斥)

有一个 \(n\times m\) 的网格图，其中有一些位置有障碍物，不能通行。

有两只乌龟同时从 \((1,1)\) 出发，前往 \((n,m)\)，并且只能向下、向右走。

要求两只乌龟除了 \((1,1),(n,m)\) 外，路径不能有相交。

问有多少种行走方案。

\(n,m\le 3000\)

$\texttt{solution}$

先考虑只有一只乌龟时怎么做：可以设 \(dp(x,y)\) 表示走到 \((x,y)\) 为止的方案数，那么直接从左边、上边两个方格转移过来即可。

不难注意到：

• 一对合法的路径一定是 \((1,2)\rightarrow(n-1,m),(2,1)\rightarrow(n,m-1)\)。

• 一对路径 \((1,2)\rightarrow(n,m-1),(2,1)\rightarrow(n-1,m)\) 一定是不合法的。

那么我们将第一种情况的答案减去第二种的情况就是答案了。

考虑一种不合法情况的最后一个交点，一定可以通过交换交点之后的路径形成上面第二种情况。

由于上面第二种情况一定不合法，而任何不合法情况都可以转化为上面第二种情况，所以第二种情况就等价于不合法情况。

之后直接 dp 就行啦。

$\texttt{code}$

#define Maxn 3005
#define mod 1000000007
typedef long long ll;
int n,m;
ll f[Maxn][Maxn][2];
char s[Maxn][Maxn];
int main()
{n=rd(),m=rd();for(int i=1;i<=n;i++) scanf("%s",s[i]+1);f[1][2][0]=(s[1][2]=='.')?1:0,f[2][1][1]=(s[2][1]=='.')?1:0;for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(i!=1 || j!=1){if((i!=1 || j!=2) && s[i][j]=='.')f[i][j][0]=(f[i][j-1][0]+f[i-1][j][0])%mod;if((i!=2 || j!=1) && s[i][j]=='.')f[i][j][1]=(f[i][j-1][1]+f[i-1][j][1])%mod;}printf("%lld\n",(f[n-1][m][0]*f[n][m-1][1]%mod-f[n][m-1][0]*f[n-1][m][1]%mod+mod)%mod);return 0;
}

CF1270E Divide Points

难度：\(\texttt{2300}\)

给你 \(n\) 个点和它们的坐标，现在给它们两两连上边，如果在同一组为黄色，不同组为蓝色。

现在让你给出任意一种分组方案，使得所有长度相同的边颜色相同，保证有解。

\(n\le 10^5\)

$\texttt{solution}$

我们考虑根据点横纵坐标之和的奇偶性来划分，因为这样不同集合的点之间距离的平方为奇数，而同一个集合内距离平方为偶数，一定不相等，可以直接划分。

那么我们将整个网格黑白染色，黑点归为一组，白点归为一组即可。

如果所有点都为黑点或都为白点怎么办？

我们首先可以将白点都向下平移一个单位使他们都变为黑点。

于是我们将整张图旋转 \(45^o\)，将 \((x,y)\) 转到 \((\frac{x+y}{2},\frac{x-y}{2})\)，保证可以不会出现小数。

如果旋转完之后还是只有黑点，那么继续旋转。

发现每次旋转都将一个点到原点的距离除以 \(2\)，所以最终旋转次数不回超过 \(\log A\)。

$\texttt{code}$

#define Maxn 1005
int n,cnt;
int pr[Maxn],x[Maxn],y[Maxn];
bool check()
{bool ex1=false,ex2=false;for(int i=1;i<=n;i++)if((x[i]+y[i])&1) ex1=true;else ex2=true;if(ex1 && ex2) return true;for(int i=1,tx,ty;i<=n;i++){if(ex2) tx=(x[i]+y[i])/2,ty=(x[i]-y[i])/2;else tx=(x[i]+y[i]-1)/2,ty=(x[i]-y[i]-1)/2;x[i]=tx,y[i]=ty;}return false;
}
int main()
{n=rd();for(int i=1;i<=n;i++) x[i]=rd(),y[i]=rd();while(!check());for(int i=1;i<=n;i++) if((x[i]+y[i])&1) pr[++cnt]=i;printf("%d\n",cnt);for(int i=1;i<=cnt;i++) printf("%d ",pr[i]);printf("\n");return 0;
}

CF1615D X(or)-mas Tree

难度：\(\texttt{2200}\)

给定一颗 \(n(n\le 2\times 10^5)\) 个点的带权树，一些权值已经确定而其他的没有确定(用 \(-1\) 表示)。

现在有 \(m(m\le 2\times 10^5)\) 条信息表示 \(u_i\) 到 \(v_i\) 的路径上的权值 \(\texttt{xor}\) 和的 popcount 为奇数还是偶数。

请你构造出这样一棵树，或者输出无解。

$\texttt{solution}$

我想到的内容：将路径上的异或和转化为两个点到根的距离的异或和，而且每改变路径上一条边的二进制位都会改变路径 popcount 的奇偶性。

之后就不 wei zhuo 啦。

核心思想：其实我们可以直接将一条边的权值根据其 popcount 的奇偶性改为 \(0\) 或 \(1\)，因为任意一位改变都会影响奇偶性。

那么所有的异或值只能为 \(0\) 或 \(1\) 了。

如果两个点之间的路径奇偶性等于 \(1\)，则这两个点到根的路径 popcount 不等；反之，则相等。

因此转化为了这样一道题：有两个集合，第 \(i\) 个条件表示 \(u\) 和 \(v\) 在同一个集合，或不在同一个集合，求出一组解。

这不就是 \(2-set\) 或扩展域并查集裸题吗？直接跑即可。

输出方案的时候看一条边上的两个点是否在同一个集合，在即 \(0\)，不在即 \(1\)。

$\texttt{code}$

#define Maxn 200005
typedef long long ll;
int T,n,m,tot=1;
int hea[Maxn<<1],nex[Maxn<<1],ver[Maxn<<1],edg[Maxn<<1],ans[Maxn<<1];
int fa[Maxn<<1];
bool Last[Maxn];
inline void add(int x,int y,int d)
{ ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot,edg[tot]=d; }
int Find(int x){ return (fa[x]==x)?x:(fa[x]=Find(fa[x])); }
inline void merge(int x,int y) { fa[Find(x)]=Find(y); }
void dfs(int x,int F)
{for(int i=hea[x];i;i=nex[i]){if(ver[i]==F) continue;if(Last[x]!=Last[ver[i]]) ans[i]=ans[i^1]=1;else ans[i]=ans[i^1]=0;dfs(ver[i],x);}
}
void solve()
{n=rd(),m=rd(),tot=1;for(int i=1;i<=n+n;i++) fa[i]=i,hea[i]=0;for(int i=1,x,y,d;i<n;i++){x=rd(),y=rd(),d=rd(),add(x,y,d),add(y,x,d);if(d!=-1){if(__builtin_popcount(d)&1) merge(x,y+n),merge(x+n,y);else merge(x,y),merge(x+n,y+n);}}for(int i=1,x,y,d;i<=m;i++){x=rd(),y=rd(),d=rd();if(d) merge(x+n,y),merge(x,y+n);else merge(x,y),merge(x+n,y+n);}for(int i=1;i<=n;i++) if(Find(i)==Find(i+n)) { printf("NO\n"); return; }for(int i=1;i<=n;i++) Last[i]=(Find(i)<=n)?1:0;dfs(1,0);printf("YES\n");for(int i=2;i<=tot;i+=2)if(edg[i]!=-1) printf("%d %d %d\n",ver[i],ver[i^1],edg[i]);else printf("%d %d %d\n",ver[i],ver[i^1],ans[i]);
}
int main()
{T=rd();while(T--) solve();return 0;
}

CF1635F Closest Pair

难度：\(\texttt{2800}\)

给定 \(n\) 个物品，每个物品有属性 \(x_i,w_i\)。\(q\) 次询问，每次给定一个区间 \([l,r]\)，求：

\[\min_{l\le i<j\le r}\{|x_i-x_j|\times (w_i+w_j)\} \]

\(1\leq n,q\leq 3\times 10^5,1\leq w\leq 10^9,|x_i|\leq 10^9\)。

保证 \(x_i<x_{i+1}\)。

$\texttt{solution}$

最终要的一个性质 \(-\) 设：

\[L_i=\max\{j|j<i,w_j<w_i\}\\ R_i=\min\{j|i<j,w_i>w_j\} \]

那么答案一定在点对 \((L_i,i),(i,R_i)\) 中间产生。

证明：比较显然吧，但是感觉比较难以发现。发现所有较优的点对都满足这个性质。

这样发现最终第 \(i\) 个询问的答案为：

\[\min_{ql\le i\le j\le qr}cal_{ij} \]

那么离线之后直接用树状数组倒着维护即可。

\(\bigstar\texttt{Trick}\)：用两个 vector 记下所有区间、询问的左端点，从大到小枚举左端点，用树状数组记下 \([0,r]\) 内最小值。对于每个询问直接在树状数组上直接查询即可。

vector<pa> query[Maxn],val[Maxn];
for(int i=1;i<=n;i++)
{val[L[i]].pb(pa(calc(L[i],i),i));val[i].pb(pa(calc(i,R[i]),R[i]));
}
for(int i=1,l,r;i<=q;i++) l=rd(),r=rd(),query[l].pb(pa(r,i));
for(int i=1;i<=n;i++)
{for(pa v:val[i]) T.add(v.se,v.fi);for(pa v:query[i]) ans[v.se]=min(ans[v.se],T.query(v.fi));
}

$\texttt{code}$

#define Maxn 300005
int n,m;
int x[Maxn],w[Maxn],tl[Maxn],tr[Maxn];
ll ans[Maxn];
vector<pa> avai[Maxn],que[Maxn];
priority_queue<int> pq;
struct BIT
{ll tree[Maxn];inline void init(){ memset(tree,0x3f,sizeof(tree)); }inline void add(int x,ll k){ while(x<=n) tree[x]=min(tree[x],k),x+=x&(-x); }inline ll query(int x){ ll ret=infll; while(x) ret=min(ret,tree[x]),x-=x&(-x); return ret; }
}T;
int main()
{n=rd(),m=rd(),T.init();for(int i=1;i<=n;i++) x[i]=rd(),w[i]=rd();pq.push(0);for(int i=1;i<=n;i++){while(w[pq.top()]>w[i]) pq.pop();tl[i]=pq.top(),pq.push(i);}while(!pq.empty()) pq.pop();pq.push(-n-1);for(int i=n;i>=1;i--){while(w[-pq.top()]>w[i]) pq.pop();tr[i]=-pq.top(),pq.push(-i);}for(int i=1;i<=n;i++){ll ttl=1ll*(x[i]-x[tl[i]])*(w[i]+w[tl[i]]);ll ttr=1ll*(x[tr[i]]-x[i])*(w[tr[i]]+w[i]);if(tl[i]) avai[tl[i]].pb(pa(ttl,i));if(tr[i]!=n+1) avai[i].pb(pa(ttr,tr[i]));}for(int i=1,ql,qr;i<=m;i++) ql=rd(),qr=rd(),que[ql].pb(pa(qr,i));memset(ans,0x3f,sizeof(ans));for(int i=n;i>=1;i--){for(pa v:avai[i]) T.add(v.se,v.fi);for(pa v:que[i]) ans[v.se]=min(ans[v.se],T.query(v.fi));}for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);return 0;
}

CF1592F1 & F2 Alice and Recoloring 1 & 2

\[\texttt{F1 - 2600} \]

给定 \(n\times m\) 的矩阵，每个格子有黑(B)或白(W)的颜色，可以实施以下四种操作：

1. 使用 \(1\) 块钱，选定一个包含 \((1,1)\) 的子矩阵，把矩阵中的颜色全部反转。
2. 使用 \(2\) 块钱，选定一个包含 \((n,1)\) 的子矩阵，把矩阵中的颜色全部反转。
3. 使用 \(4\) 块钱，选定一个包含 \((1,m)\) 的子矩阵，把矩阵中的颜色全部反转。
4. 使用 \(3\) 块钱，选定一个包含 \((n,m)\) 的子矩阵，把矩阵中的颜色全部反转。

问吧所有格子都变成白色的最小代价。

\[\texttt{F2 - 2800} \]

给定 \(n\times m\) 的矩阵，每个格子有黑(B)或白(W)的颜色，可以实施以下四种操作：

1. 使用 \(1\) 块钱，选定一个包含 \((1,1)\) 的子矩阵，把矩阵中的颜色全部反转。
2. 使用 \(3\) 块钱，选定一个包含 \((n,1)\) 的子矩阵，把矩阵中的颜色全部反转。
3. 使用 \(4\) 块钱，选定一个包含 \((1,m)\) 的子矩阵，把矩阵中的颜色全部反转。
4. 使用 \(2\) 块钱，选定一个包含 \((n,m)\) 的子矩阵，把矩阵中的颜色全部反转。

问把所有格子都变成白色的最小代价。

\(n,m\le 500\)。

$\texttt{solution}$

\[\texttt{F1 - solution} \]

对于代价为 \(2\) 的 \(2\) 操作，我们完全可以用两次代价为 \(1\) 的 \(1\) 操作代替。

对于代价为 \(4\) 的 \(3\) 操作，我们也可以用用两次代价为 \(1\) 的 \(1\) 操作代替。

所以我们只用 \(1\) 和 \(4\) 操作就可以完成所有移动了。

\(\bigstar\texttt{Trick}\)：发现 \(1\) 和 \(4\) 操作需要整个矩阵翻转，不方便操作，考虑构造新矩阵 \(a_{i,j}=c_{i,j}\oplus c_{i,j+1}\oplus c_{i+1,j}\oplus c_{i+1,j+1}\)，那么所有格子都为 \(0\) 的充要条件就是 \(a_{i,j}\) 都为 \(0\)。

发现在新矩阵中，操作 \(1\) 就是用 \(1\) 的代价将 \(a_{x,y}\) 取反，操作 \(3\) 就是用 \(3\) 的代价将 \(a_{x-1,y-1},a_{x-1,m},a_{n,y-1},a_{n,m}\) 都取反。

发现操作 \(3\) 比操作 \(1\) 影响的格子多了一个，但是，如果反复使用操作 \(3\)，\(a_{n,m}\) 会被反复取反，所以操作 \(3\) 最多使用一次，且必须在使用前四个格子都是 \(1\) 才能够减小代价。直接贪心即可。

\[\texttt{F2 - solution} \]

继续沿用上面的思路，将 \(c\) 重构为 \(a\)，仍旧只可能使用 \(1,4\) 操作。

\(\bigstar\texttt{Hint}\)：发现上面使用操作 \(3\) 当且仅当 \(a_{x,y},a_{x,m},a_{n,y}\) 都为 \(1\) 时才使用依然成立，但是不用限制 \(a_{n,m}\) 了。

假设我们使用在 \((x,y) - (n,m)\) 的操作 \(3\)，第 \(x\) 行与第 \(y\) 列必然会变为 \(0\)，操作 \(3\) 一定不会再次对 \(x\) 行 \(y\) 列使用。

所以可以对 \(x\) 行 \(y\) 列进行匹配，匹配成功一对答案就减小 \(1\)，上个网络流即可。

CF79D Password

难度：\(\texttt{2800}\)

有一段长度为 \(n(n\le 40000)\) 的灯泡序列，其中有 \(k(k\le 10)\) 盏是灭的，其他都是亮着的。由于你比较懒，所以只愿意选择长度为 \(a_i\) 的区间将区间内所有灯泡明暗状态取反。所有可能 \(a_i\) 的个数为 \(l(l\le 100)\)。

问最终将所有灯泡点亮的最少步数。

$\texttt{solution}$

显然需要对整个序列差分，将区间操作变为同时将两个数取反。

发现 \(k\) 非常小，差分后为 \(1\) 的点一定不会超过 \(20\) 个，可以直接将他们压起来。

列对于一个状态，我们枚举两个点并将他们加入集合中，转移方程为：

\[dp_{s|i|j}=\max\{dp_s+Cost(i,j)\} \]

\(Cost(i,j)\) 表示同时反转 \(i,j\) 两个点需要的最小步数，预处理即可。

这样复杂度是 \(\mathcal{O(2^k k^2)}\) 的，完全不行捏。

有一个转移上的小技巧：直接钦定下一次选择 \(s\) 中最小的且没有被选择的点必选，这样就少掉一只 \(k\)。

CF19E Fairy

难度：\(\texttt{2900}\)

给定一张无向图，问有哪些边(只删一条边)被删除后，图会变成一张二分图。

\(n,m\le 10^5\)。

$\texttt{solution}$

变成二分图，也就是没有大小为奇数的环。

受到 [WC2011]最大XOR和路径 的启发，先搞下一棵生成树，那么每一条非树边都对应着一个环。

我们称一条非树边是好的，当且仅当它直接形成的环大小为偶数；称一条非树边是坏的，当且仅当它直接形成的环大小为奇数。

我们称一条非树边将它形成的环上的树边覆盖。

由于删去一条边需要去掉所有的奇环，所以这些边必须覆盖所有的奇环。

\(\bigstar\texttt{Trick}\)：有一个结论：可以删去的边一定被所有坏边覆盖，并且不被任何好边覆盖。

证明：被所有坏边覆盖可以保证去掉奇环，不被好边覆盖放置一个偶环和一个奇环形成了另一个奇环。

所以每次遇到一奇环就将路径上的边边权 \(+1\)，遇到偶环就 \(-1\)，那么最终答案就是边权等于奇环个数的边。

CF1239E Turtle 咕

难度：\(\texttt{3100}\)

咕咕咕

CF1609F Interesting Sections

难度：\(\texttt{2800}\)

给你一个长为 \(n\) 的非负整数序列 \(a\)，求有多少区间 \([l,r]\) 满足 \(\text{popcount}(\max\limits_{i=l}^r a_i)=\text{popcount}(\min\limits_{i=l}^r a_i)\)。

\(1\le n\le 10^6,0\le a_i\le 10^{18}\)。

$\texttt{solution}$

\(\bigstar\texttt{Trick}\)：遇到数区间的问题要么是分治要么就是固定端点，这道题固定端点。

而这种和最大、最小值有关的可以进一步总结为：从前往后扫 \(i\)，用单调栈 \(+\) 数据结构维护 \([x,i]\) 的最大值以及最小值，具体的，单调栈的每一次入栈和出栈可以看成一个区间赋值，使用线段树即可。

考虑枚举 \(\text{popcount}\)，在每个 \(r\) 端点，找出所有最大值满足条件的 \(l_1\) 和最小值满足条件的 \(l_2\) 的集合。

显然只有这个数本身 \(\text{popcount}\) 满足条件才有可能作为答案，而且从左导游枚举 \(r\) 端点的时候一定有满足条件的 \(l\) 在向右移动，可以用单调栈配合线段树(维护现在那些位置合法)解决上面的问题。

那么现在我们对于一个 \(r\)，需要计算两个两个条件都满足的端点数量。如果在上面线段树中记答案为 \(1\) 表示合法，那么就是需要统计答案为 \(2\) 的点的个数。由于这道题加减的性质比较优美，直接记录 \(0,1,2\) 的个数即可。

优化：当没有 \(\text{popcount}(a_i)=p\) 时，不用判断这一种情况。

shabi 吗？指令集 \(+\)fread\(+\) 优化才能过！！

CF773D Perishable Roads

难度：\(\texttt{2700}\)。

$\texttt{solution}$

发现最终形态是一棵树加上一条从最短边出发的链，而最终答案只和在链上的答案和树上的点数有关，且链上答案越小越好。

我们计算从最小边出发，到达每个“终点”，也就是以他们作为根的时候的答案的链上权值。

不烦设链上有 \(x\) 个点，树上有 \(n-x-1\) 个点，最小边权值为 \(v\)，链上的答案为 \(ds_t\)，则当前答案为 \((n-x-1)\times v+ds_t\)。

但是其中的 \(x\) 让我们感到不爽，将所有边权减去 \(v\)，计算这样的表达式：\((n-x-1)\times v+(ds_t'+x\times v)=(n-1)\times v+ds_t'\)。

这样只用求出到每个终点的权值即可。

那么赋每个点初始距离为 \(ds_{t}=2\min_i(g_{i,t})\)，求最短路即可。

CF1453F Even Harder

$\texttt{solution}$

由于在最终留下了一个序列，不妨在序列上 DP，设 \(dp_{i,j}\) 表示当前在 \(i\)，上一个在 \(j\) 的最少删除点数，那么再上一个 \(k\) 是一个前缀，前缀优化即可。

CF799F Beautiful fountains rows

$\texttt{solution}$

奇数和 \(0\) 不相容，考虑将奇数的条件转化。

区间 \([l,r]\) 改为在 \([l,r-1]\) 区间内加上 \(1\)，如果询问区间 \([l,r]\) 满足 \([l,r-1]\) 内的和为偶数，则这是合法的区间。

之后就异或哈希，记得判掉 \(0\) 即可。

CF1747E List Generation

$\texttt{solution}$

显然差分，考虑容斥计算方案数。最终式子如下：

\[\sum_{i=1}^{n+m}\dbinom{n+i-1}{n}\dbinom{m+i-1}{m}(i+1)\sum_{j=0}^{n+m-i}(-1)^j\dbinom{i+j+1}{j} \]

那么可以根据 \(j\) 的奇偶性分开推导，如果要容易一些转移可以写出杨辉三角，得到转移方程。