后缀数组 SA

后缀树组(SA，suffix array)，用于处理字符串子串形成的结构。

处理子串的结构主要方式有：后缀数组 SA，后缀自动机 SAM，后缀树 ST。

后缀树和后缀自动机暂时决定咕咕咕，以后学习可以参考ix35 的字符串复习。

含义与实现

后缀

我们定义长度为 \(n\) 的字符串 \(s\) 编号为 \(l\) 的后缀为 \(s\) 在 \([l,s]\) 上的字串，记 \(l\)(即起始位置)为该后缀的编号。

后缀树组

如果将 \(s\) 所有 \(n\) 个后缀提取出来，按照字典序升序排序，后缀数组 \(\text{SA}_i\) 定义为排名为 \(i\) 的后缀的编号。

那么怎么求出一个字符串的后缀数组呢？

求解

显然暴力找出 \(n\) 个后缀再快速排序的 \(\mathcal{O(n^2\log n)}\) 的(加上比较的复杂度)，不够优美。

一般采用 Manber 和 Myers 发明的类似于倍增的方法求解。

(下面图片来自jinkun113 - 后缀数组，如有侵权请告知删除)

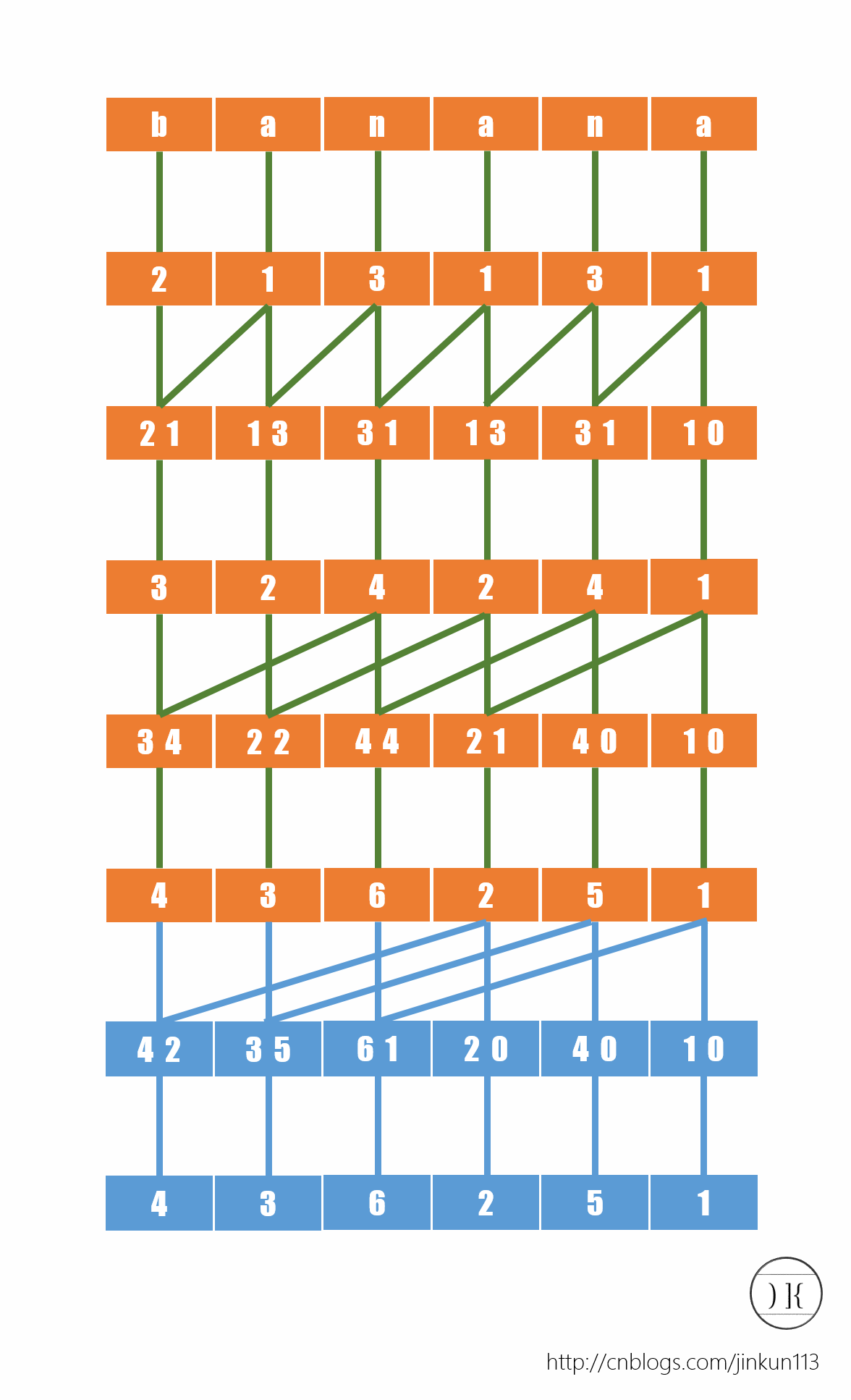
如上图，类似每次将两端字符串拼起来形成新的字符串，类似高低进制拼接后再一次排序得到。

通过这样的操作，以 \(i\) 为开头的字串会不断增长到两倍(大于 \(n\) 的用空字符补齐)，即不断溢出，最终就得到了 \(n\) 个后缀。

类似这样的倍增求解的方法还可以用于其他的问题，如CF1654F Minimal String Xoration。

实现

在上面的过程中，记在 \(i\) 位置上合并的两个数高位的是 \(x_i\)，低位的是 \(y_i\)，他们记录的是这一部分字串的排名，最终再一次排序后的排名记在 \(x\) 数组内。

这样非常容易写出一个 \(\mathcal{O(n\log^2 n)}\) 的解法，具体就是每次将两端字串合并后，给 \(i\) 赋值为 \(x_i,y_i\) 高低位相接。之后再一次排序并离散化就可以得到新的排名。

//暴力O(n\log^2 n)
int MAX;
int sa[Maxn],First[Maxn],Second[Maxn];
bool cmp(int x,int y)
{if(First[x]==First[y]) return Second[x]<Second[y];return First[x]<First[y];
}
inline void Get_Rank()
{memset(First,0,sizeof(First)),MAX=n;for(int i=1;i<=n;i++) sa[i]=i;for(int i=1;i<=n;i++) First[i]=s[i],Second[i]=0;sort(sa+1,sa+n+1,cmp);for(int p=1;p<=n;p<<=1){for(int i=1;i<=n;i++) Second[i]=First[i+p];sort(sa+1,sa+n+1,cmp),swap(Second,First),MAX=First[sa[1]]=1;for(int i=2;i<=n;i++)if(Second[sa[i]]!=Second[sa[i-1]] || Second[sa[i]+p]!=Second[sa[i-1]+p])First[sa[i]]=++MAX;else First[sa[i]]=MAX;if(MAX==n) return;}
}

如果要进一步优化复杂度，可以用基数排序代替上面的快速排序，大致步骤如下：

先将 \(n\) 个串的第二关键字排序。即，先将 \(p\) 个空串放在最前面，再按照上一次排完的取。
再将第一关键塞入桶中，对他们排序记录每一个第一关键字对应最终排名的区间，再用已经排序完的第二关键字去对应他们。
最后根据后缀树组重构 \(\text{Rank}\) 数组，即每个字串的排名，记得去重即可。

P3809 【模板】后缀排序

//O(n\log n)
inline void Sort()
{for(int i=1;i<=MAX;i++) cnt[i]=0;for(int i=1;i<=n;i++) cnt[Rank[tmp[i]]]++;for(int i=1;i<=MAX;i++) cnt[i]+=cnt[i-1];for(int i=n;i>=1;i--) sa[cnt[Rank[tmp[i]]]--]=tmp[i],tmp[i]=0;
}
inline void Get_SA()
{for(int i=1;i<=n;i++) Rank[i]=s[i],tmp[i]=i;MAX=255,Sort();for(int p=1;p<=n;p<<=1){int num=0;for(int i=n-p+1;i<=n;i++) tmp[++num]=i;for(int i=1;i<=n;i++) if(sa[i]>p) tmp[++num]=sa[i]-p;Sort(),swap(Rank,tmp),MAX=Rank[sa[1]];for(int i=2;i<=n;i++)if(tmp[sa[i]]!=tmp[sa[i-1]] || tmp[sa[i]+p]!=tmp[sa[i-1]+p])Rank[sa[i]]=++MAX;else Rank[sa[i]]=MAX;if(MAX==n) return;}
}

基础运用

说了这么多，后缀数组到底有什么用呢？

多模式匹配

回忆AC 自动机，它常用于多模式串匹配文本串的问题，复杂度为 \(\mathcal{O(n)}\) 的，~~相较而言后缀数组就显得比较逊~~。

我们对文本串建立后缀树组，将所有后缀利用后缀树组按照字典序排序。

对于每一个模式串，在所有后缀中二分并 \(\mathcal{O(n)}\) 检查，匹配一个的复杂度是 \(\mathcal{O(m\log n)}\)，\(m\) 是模式串长度， \(n\) 是文本穿长度。

最长公共前缀(LCP)

只有一个 \(\text{SA}\) 数组能够完成的事情非常有限，所以通常需要用到两个辅助数组 \(\text{Hight,Rank}\)。

\(\text{Rank}\) 表示后缀 \(i\) 在所有后缀中的排名(即上面定义中使用的 \(x\) 数组)。

\(\text{Height}\) 表示 \(\text{SA}_{i-1},\text{SA}_{i}\) 两个子串的 LCP(Longesr Common Prefix)长度。

\(\text{Rank}\) 比较好求，那么 \(\text{Height}\) 怎么求出呢？

有一个非常重要的定理：设 \(h_i=\text{Height}(\text{SA}_i)\)，一定有：(不会证明)

\[h_i\ge h_{i-1}-1 \]

有了这个结论就可以快速求出每个 \(\text{Height}\) 了。

两个后缀的 LCP 就是 \(\min\{\text{Height}_k\}(k\in(i,j])\)。

inline void Get_Height()
{for(int i=1,j,tmp=0;i<=n;i++){if(Rank[i]==1) { Height[Rank[i]]=0; continue; }if(tmp) tmp--;j=sa[Rank[i]-1];while(i+tmp<=n && j+tmp<=n && s[i+tmp]==s[j+tmp]) tmp++;Height[Rank[i]]=tmp;}
}

例题

SP694 Distinct Substrings

给定一个长度为 \(n(n\le 10^6)\) 的字符串，求出该字符串有多少个本质不同的字串。(虽然原题 \(n\) 只有 \(1000\))

\(\text{Height}\) 数组的含义是排名为 \(i\) 的后缀和排名第 \(i-1\) 的后缀的 LCP 长度，我们发现这个长度正好是以 \(\text{SA}_i\) 开头和以 \(\text{SA}_{i-1}\) 开头的字串算重的数量。所以最终的式子就是：

\[\dfrac{n\times(n+1)}{2}-\sum_{i=2}^{n}\text{Height}_i \]

复杂度 \(\mathcal{O(n\log n)}\)。

P2852 [USACO06DEC]Milk Patterns G

给定字符集大小为 \(10^6\) 且长度为 \(n(n\le 2\times 10^4)\) 的字符串 \(s\)，给定循环次数 \(k(k\le n)\)，找出在字符串中至少循环 \(k\) 次(可以由重叠)的字串的最大长度。

考虑求出字符串的 \(\text{Height}\)，那么答案就是所有长度为 \(k\) 的 \(\text{Height}\) 数组子区间中数的最小值中的最大值。

P3181 [HAOI2016]找相同字符

给定两个长度分别不大于 \(2\times 10^5\) 的字符串，求出在两个字符串中各取出一个子串使得这两个子串相同的方案数。两个方案不同当且仅当这两个子串中有一个位置不同。

不会了

\(\bigstar\texttt{Hint}\)：考虑从一个串中取出两个子串使得他们相同的方案数，就是这个串所有后缀两两之间的 LCP 长度之和。

那么考虑将两个串拼在一起，当然中间需要加上一个奇怪的字符，计算方案数。

当然这样会算上来自同一个串的情况，所以需要将每个串单独计算后减去贡献。

那么上面的贡献如何计算？其实需要求的是 \(\text{Height}\) 中所有子区间的区间最小值的和。

\(\bigstar\texttt{Trick}\)：要计算一个长度不超过 \(10^5\) 的序列所有子区间的最小值的和，可以用单调栈解决。考虑从前往后加入每一个元素，显然如果有前面的元素大于这个元素，前面的元素的值以后都没用了。维护一个递增的单调栈，并记录这个元素中原本包含的元素个数，同时统计这个单调栈的权值之和，每次累计即可。

\(\bigstar\texttt{Important}\)：注意分隔符不要用 \0，可以用 \(z+1\) 等等。

P4070 [SDOI2016]生成魔咒

原本有一个空串，有 \(n\) 次操作，每次向串尾加入一个字符，字符集 \(10^9\)，同时询问本质不同字串数量。

\(n\le 10^5\)。

\(\bigstar\texttt{Trick}\)：倒置字符串！！！

如果我们每次向串首加入一个字符，只新产生了一个后缀，不用考虑对所有后缀的影响。

但是如果我们每次重新维护 \(\text{Rank}\) 和 \(\text{Height}\) 的话，还是会非常难做，所以用 \(\text{Rank}\) 的相对大小维护下面的 \(\text{Rank}\) 比它小、大的后缀。

先对倒置后的整个字符串求一遍 \(\text{Rank}\) 和 \(\text{Height}\)，由于我们需要求的是包含新加入字符的子串中，重复出现的字串个数，可以直接和已经加入的后缀中 \(\text{Rank}\) 离它最近的(用 set，除非你想打一个 Splay)，并求出重复的长度。

SP1811 LCS - Longest Common Substring

给定两个长度不超过 \(2.5\times 10^5\) 的字符串，求出他们的 LCS。两个字符串的 LCS 是他们的最长公共子串。

好像把两个串用奇怪的字符合起来，再记录每一个 \(\text{Rank}\) 大于它的和它来自不同字符串的位置，求 LCP 长度即可。

P5341 [TJOI2019]甲苯先生和大中锋的字符串

给定长度不超过 \(10^5\) 的字符串和重复次数 \(k\)，记 \(cnt_i\) 表示长度 \(s\) 所有长度为 \(i\) 的子串中恰好在 \(s\) 中出现 \(k\) 次的子串数量。问 \(cnt_i\) 最大的 \(i\)。

不会了

\(\bigstar\texttt{Hint}\)：考虑 \(R=\min_{i=l}^{l+k-1}{\text{Height}_i}\) 什么时候不能作为答案，记 \(L=\max(\text{Height}_{l-1},\text{Height}_{i+k})\)，则一定有当 \(1\le len\le L\) 时，长度为 \(len\) 的子串出现次数大于 \(k\) 次。则可以选择的去长度为 \((L,R]\)。

注意一下 \(k=1\) 的特判，其他用单调队列维护即可。

\(\bigstar\texttt{Important}\)：注意初始化的时候需要将 \(\text{Height}_{n+1}\) 初始化为 \(0\)！！！