今天选择写这篇博客主要是为了告诉大家一个道理，数组比$vector$快太多了，我这两道题第一次都因为$vector$，$T$到飞起

T1：Housewife Wind

题目

After their royal wedding, Jiajia and Wind hid away in XX Village, to enjoy their ordinary happy life. People in XX Village lived in beautiful huts. There are some pairs of huts connected by bidirectional roads. We say that huts in the same pair directly connected. XX Village is so special that we can reach any other huts starting from an arbitrary hut. If each road cannot be walked along twice, then the route between every pair is unique.

Since Jiajia earned enough money, Wind became a housewife. Their children loved to go to other kids, then make a simple call to Wind: ‘Mummy, take me home!’

At different times, the time needed to walk along a road may be different. For example, Wind takes 5 minutes on a road normally, but may take 10 minutes if there is a lovely little dog to play with, or take 3 minutes if there is some unknown strange smell surrounding the road.

Wind loves her children, so she would like to tell her children the exact time she will spend on the roads. Can you help her?
Input
The first line contains three integers n, q, s. There are n huts in XX Village, q messages to process, and Wind is currently in hut s. n < 100001 , q < 100001.

The following n-1 lines each contains three integers a, b and w. That means there is a road directly connecting hut a and b, time required is w. 1<=w<= 10000.

The following q lines each is one of the following two types:

Message A: 0 u
A kid in hut u calls Wind. She should go to hut u from her current position.
Message B: 1 i w
The time required for i-th road is changed to w. Note that the time change will not happen when Wind is on her way. The changed can only happen when Wind is staying somewhere, waiting to take the next kid.
Output
For each message A, print an integer X, the time required to take the next child.
Sample Input
3 3 1
1 2 1
2 3 2
0 2
1 2 3
0 3
Sample Output
1
3

题解

其实这道题就是一个边权模板题，这篇博客的重点是后面的染色
其次这道题我被卡了$vector$所以来记录一下数组版怎么写罢了vector版边权模板
我觉得没有什么讲的必要，直接上就行了，如果刚刚踏入门的话，→移步入门树链剖分

code

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define maxn 100005
struct noded {int u, v;int w;noded () {}noded ( int U, int V, int W ) {u = U;v = V;w = W;}
}tmp[maxn];
struct EDGE {int to, next;
}edge[maxn << 1];
int cnt = 1, n, q, s;
int f[maxn], son[maxn], dep[maxn], Size[maxn];
int id[maxn], Top[maxn];
int tree[maxn << 2];
int head[maxn];void update ( int t, int l, int r, int idx, int val ) {if ( l == r ) {tree[t] = val;return;}int mid = ( l + r ) >> 1;if ( idx <= mid )update ( t << 1, l, mid, idx, val );elseupdate ( t << 1 | 1, mid + 1, r, idx, val );tree[t] = tree[t << 1] + tree[t << 1 | 1];
}int query ( int t, int l, int r, int L, int R ) {if ( L <= l && r <= R )return tree[t];int mid = ( l + r ) >> 1;int ans = 0;if ( L <= mid )ans += query ( t << 1, l, mid, L, R );if ( mid < R )ans += query ( t << 1 | 1, mid + 1, r, L, R );return ans;
}void addedge ( int u, int v ) {edge[cnt].to = v;edge[cnt].next = head[u];head[u] = cnt ++;
}void dfs1 ( int u, int fa, int depth ) {f[u] = fa;dep[u] = depth;Size[u] = 1;for ( int i = head[u];i != -1;i = edge[i].next ) {int v = edge[i].to;if ( v == fa )continue;dfs1 ( v, u, depth + 1 );Size[u] += Size[v];if ( Size[v] > Size[son[u]] || ! son[u] )son[u] = v;}
}void dfs2 ( int u, int t ) {Top[u] = t;id[u] = ++ cnt;if ( ! son[u] )return;dfs2 ( son[u], t );for ( int i = head[u];i != -1;i = edge[i].next ) {int v = edge[i].to;if ( v != son[u] && v != f[u] )dfs2 ( v, v );}
}int solve ( int x, int y ) {int ans = 0;int fx = Top[x], fy = Top[y];while ( fx != fy ) {if ( dep[fx] > dep[fy] ) {ans += query ( 1, 1, n, id[fx], id[x] );x = f[fx];fx = Top[x];}else {ans += query ( 1, 1, n, id[fy], id[y] );y = f[fy];fy = Top[y];}}if ( id[x] < id[y] )ans += query ( 1, 1, n, id[x] + 1, id[y] );elseans += query ( 1, 1, n, id[y] + 1, id[x] );return ans;
}int main() {scanf ( "%d %d %d", &n, &q, &s );memset ( head, -1, sizeof ( head ) );for ( int i = 1;i < n;i ++ ) {scanf ( "%d %d %d", &tmp[i].u, &tmp[i].v, &tmp[i].w );addedge ( tmp[i].u, tmp[i].v );addedge ( tmp[i].v, tmp[i].u );}cnt = 0;//建边的时候不小心用到了，一定要清零 dfs1 ( 1, 0, 1 );dfs2 ( 1, 0 );for ( int i = 1;i < n;i ++ ) {if ( dep[tmp[i].u] > dep[tmp[i].v] )swap ( tmp[i].u, tmp[i].v );update ( 1, 1, cnt, id[tmp[i].v], tmp[i].w );}int opt, x, w;for ( int i = 1;i <= q;i ++ ) {scanf ( "%d %d", &opt, &x );if ( opt ) {scanf ( "%d", &w );update ( 1, 1, n, id[tmp[x].v], w );}else {printf ( "%d\n", solve ( s, x ) );s = x;//注意接完孩子后，mom就待在了那里}}return 0;
}

T2：染色

题目

给定一棵有n个节点的无根树和m个操作，操作有2类：
1、将节点a到节点b路径上所有点都染成颜色c；
2、询问节点a到节点b路径上的颜色段数量（连续相同颜色被认为是同一段），
如“112221”由3段组成：“11”、“222”和“1”。
请你写一个程序依次完成这m个操作。
Input
第一行包含2个整数n和m，分别表示节点数和操作数；
第二行包含n个正整数表示n个节点的初始颜色
下面 行每行包含两个整数x和y，表示x和y之间有一条无向边。
下面 行每行描述一个操作：
“C a b c”表示这是一个染色操作，把节点a到节点b路径上所有点（包括a和b）都染成颜色c；
“Q a b”表示这是一个询问操作，询问节点a到节点b（包括a和b）路径上的颜色段数量。
Output
对于每个询问操作，输出一行答案。

Sample Input
6 5
2 2 1 2 1 1
1 2
1 3
2 4
2 5
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5
Sample Output
3
1
2
Hint
数$N<=10^5$，操作数$M<=10^5$，所有的颜色C为整数且在[0, 10^9]之间。

题解

其实这道题说难也不难，简单也不简单

---

首先这个是点权题，降低了一定难度，其次改颜色的操作也是模板，我们直接进入如何统计颜色段数

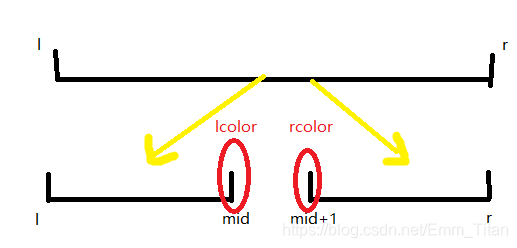
可以知道当两个区间进行合并的时候，交接处如果颜色相同的话，就并成了一段颜色，所以我们就要在线段树时判断，可以返回一个结构体带三个参数最左边的颜色最右边的颜色和颜色的段数

然后就是树链剖分的时候我们要记录上一次的左右颜色，分别于两个点的左右进行合并判断，这里主要是考察码力，可以直接看$solve$函数，我稍微改变了一下写法

code

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define maxn 100005
#define INF 0x7f7f7f7f
struct node {//用vector太慢了 int next, v;
}edge[maxn << 1];
struct noded {int lcolor, rcolor, sum;
}tree[maxn << 2];
int head[maxn], tag[maxn << 2];
int cnt;
int f[maxn], son[maxn], dep[maxn], Size[maxn];
int id[maxn], top[maxn];
int color[maxn];void addedge ( int x, int y ) {cnt ++;edge[cnt].next = head[x];edge[cnt].v = y;head[x] = cnt;
}void pushdown ( int t ) {//不用lazy标记要超时 if ( ! tag[t] )return;tree[t << 1].lcolor = tree[t << 1].rcolor = tree[t << 1 | 1].lcolor = tree[t << 1 | 1].rcolor = tag[t];tag[t << 1] = tag[t << 1 | 1] = tag[t];tag[t] = 0;tree[t].sum = tree[t << 1].sum = tree[t << 1 | 1].sum = 1;
}void update ( int t, int l, int r, int L, int R, int v ) {if ( L <= l && r <= R ) {tree[t].lcolor = tree[t].rcolor = tag[t] = v;tree[t].sum = 1;return;}pushdown ( t );int mid = ( l + r ) >> 1;if ( L <= mid )update ( t << 1, l, mid, L, R, v );if ( mid < R )update ( t << 1 | 1, mid + 1, r, L, R, v );tree[t].sum = tree[t << 1].sum + tree[t << 1 | 1].sum;if ( tree[t << 1].rcolor == tree[t << 1 | 1].lcolor )//判断左右儿子的相接处是否颜色一样 tree[t].sum --;tree[t].lcolor = tree[t << 1].lcolor;tree[t].rcolor = tree[t << 1 | 1].rcolor;
}noded query ( int t, int l, int r, int L, int R ) {if ( L <= l && r <= R )return tree[t];int mid = ( l + r ) >> 1;pushdown ( t );if ( R <= mid )return query ( t << 1, l, mid, L, R );else if ( mid < L )return query ( t << 1 | 1, mid + 1, r, L, R );else {noded ans, ans1 = query ( t << 1, l, mid, L, R ), ans2 = query ( t << 1 | 1, mid + 1, r, L, R );ans.lcolor = ans1.lcolor;ans.rcolor = ans2.rcolor;ans.sum = ans1.sum + ans2.sum;if ( ans1.rcolor == ans2.lcolor )ans.sum --;return ans;}
}void dfs1 ( int u, int fa, int depth ) {f[u] = fa;dep[u] = depth;Size[u] = 1;for ( int i = head[u];i != -1;i = edge[i].next ) {int v = edge[i].v;if ( v == fa )continue;dfs1 ( v, u, depth + 1 );Size[u] += Size[v];if ( Size[v] > Size[son[u]] || ! son[u] )son[u] = v;}
}void dfs2 ( int u, int t ) {top[u] = t;id[u] = ++ cnt;if ( ! son[u] )return;dfs2 ( son[u], t );for ( int i = head[u];i != -1;i = edge[i].next ) {int v = edge[i].v;if ( v != son[u] && v != f[u] )dfs2 ( v, v );}
}void solve ( int x, int y ) {int ans = 0, fx = top[x], fy = top[y];int xcolor = -1, ycolor = -1;noded ret;while ( fx != fy ) {if ( id[fx] < id[fy] ) {swap ( x, y );swap ( fx, fy );swap ( xcolor, ycolor );}ret = query ( 1, 1, cnt, id[fx], id[x] );ans += ret.sum;if ( ret.rcolor == xcolor )ans --;xcolor = ret.lcolor;x = f[fx];fx = top[x];}if ( id[x] > id[y] ) {swap ( x, y );swap ( xcolor, ycolor );}ret = query ( 1, 1, cnt, id[x], id[y] );ans += ret.sum;if ( xcolor == ret.lcolor )ans --;if ( ycolor == ret.rcolor )ans --;printf ( "%d\n", ans );
}void solve_update ( int x, int y, int c ) {int fx = top[x], fy = top[y];while ( fx != fy ) {if ( dep[fx] >= dep[fy] ) {update ( 1, 1, cnt, id[fx], id[x], c );x = f[fx];fx = top[x];}else {update ( 1, 1, cnt, id[fy], id[y], c );y = f[fy];fy = top[y];}}if ( id[x] <= id[y] )update ( 1, 1, cnt, id[x], id[y], c );elseupdate ( 1, 1, cnt, id[y], id[x], c );
}int main() {int n, m;memset ( head, -1, sizeof ( head ) );scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ )scanf ( "%d", &color[i] );for ( int i = 1;i < n;i ++ ) {int a, b;scanf ( "%d %d", &a, &b );addedge ( a, b );addedge ( b, a );}cnt = 0;dfs1 ( 1, 0, 1 );dfs2 ( 1, 0 );for ( int i = 1;i <= n;i ++ )update ( 1, 1, cnt, id[i], id[i], color[i] );char opt[2];int a, b, c;for ( int i = 1;i <= m;i ++ ) {scanf ( "%s %d %d", opt, &a, &b );if ( opt[0] == 'C' ) {scanf ( "%d", &c );solve_update ( a, b, c );}else solve ( a, b );}return 0;
}

看不懂的欢迎评论