图片转载自： https://blog.csdn.net/weixin_43346722/article/details/118435430

题目描述

平面上有 n个点，用n个大小相同的圆分别将一个点作为圆心，同时满足圆圈不相交，求圆的最大半径。

数据范围

$2<=n<=2e5$

解析

把题目抽象一下就是求最小的一对点的距离除以2
考虑如何求呢？
暴力当然是会T飞的
首先把所有点按x排序
然后考虑分治
分治的关键是如何把两个小问题合并
暴力合并还是n方…
我们考虑剪掉一些不必要的比较
设两边分别得到的答案的最小值为a
那么x距离大于a的肯定不用比了
但是一旦x的距离全在a里面咋办？
同理，我们按y再排一下序，y的距离大于a都不用算了
那么每个点对应的的计算范围大概就是这样：

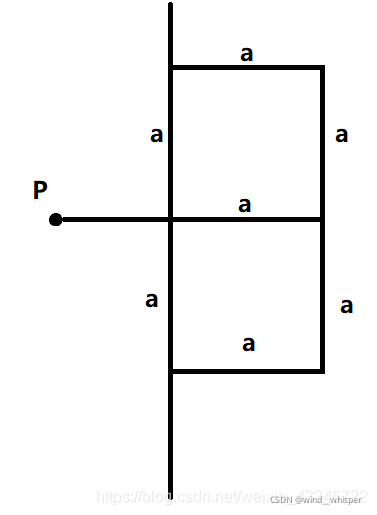
那么这样就不会有很多点了吗？
我们还有一个了一个关键性质：左边和右边的点各自之间的距离都不小于a
那么右边这个矩形里能填的两两距离不小于a的点就不多了
关于这个，我们就要使用神奇的鸽巢原理
考虑矩形按照下面这个图分区：

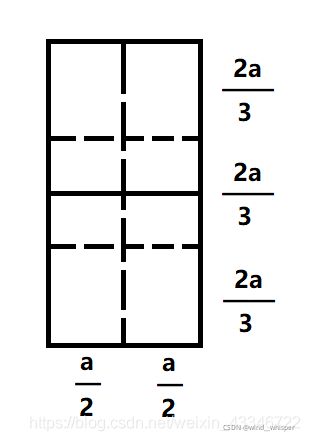
每个小矩形的对角线长度小于a，所以每个矩形最多有一个点
所以大矩形内的点不超过6个
（同时我们把6个点放到四角和两长边的终点，其实也就可以构造出6个的方案）
所以我们每个点需要计算的点最多不超过6个
时间复杂度降为线性，问题得以解决
整体复杂度：$nlogn$（每次合并按ysort可能再大一些？）

代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
const int M=2e6+100;
#define ll long long
ll read(){ll x=0,f=1;char c=getchar();while(!isdigit(c)){if(c=='-')f=-1;c=getchar();};while(isdigit(c)){x=x*10+c-'0';c=getchar();};return x*f;
}
int n,m;
struct node{double x,y;
}p[N],tmp[N],now[N];
bool cmpx(node a,node b){return a.x<b.x;}
bool cmpy(node a,node b){return a.y<b.y;}
double dis(node a,node b){//printf("  dis:");print(a);print(b);printf("%lf+%lf=%lf")return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
void print(node o){printf("(%.2lf %.2lf)",o.x,o.y);}
double solve(int l,int r){if(l==r) return 2e9;int mid=(l+r)>>1;double res=min(solve(l,mid),solve(mid+1,r));int num=0,tot=0;for(int i=mid+1;i<=r;i++){if(p[i].x-p[mid].x>=res) break;tmp[++num]=p[i];//printf("tmp:");print(p[i]);putchar('\n');}for(int i=mid;i>=l;i--){if(p[mid+1].x-p[i].x>=res) break;now[++tot]=p[i];//printf("now:");print(p[i]);putchar('\n');}sort(tmp+1,tmp+1+num,cmpy);sort(now+1,now+1+tot,cmpy);int pre=1;for(int i=1;i<=tot&&pre<=num;i++){while(pre<=num&&now[i].y-tmp[pre].y>=res) pre++;for(int j=pre;tmp[j].y-now[i].y<res&&j<=num;j++){//printf("i=%d j=%d dis=%.2lf",i,j,dis(now[i],tmp[j]));print(now[i]);print(tmp[j]);putchar('\n');res=min(res,dis(now[i],tmp[j]));}}return res;
}
int main(){while(1){n=read();if(n==0) return 0;for(int i=1;i<=n;i++){scanf("%lf%lf",&p[i].x,&p[i].y);}sort(p+1,p+1+n,cmpx);printf("%.2lf\n",solve(1,n)/2);}return 0;
}
/*
2 
0 0 
1 1 
2 
1 1 
1 1 
3 
-1.5 0 
0 0 
0 1.5 
0
*/