前言

Ubuntu是一个以桌面应用为主的开源GNU/Linux操作系统，应用很广。本篇主要讲述Ubuntu下使用SSH远程登录并安装Docker，并且提供了Docker安装的两种方式，希望对大家有所帮助。

拥抱Linux，大家可以从Ubuntu开始！

Ubuntu下安装Docker

首先我们需要准备一个Ubuntu的环境。这里笔者推荐使用Hyper-V来快速安装Ubuntu。

使用Hyper-V快速安装Ubuntu

这里笔者推荐使用Hyper-V快速安装Ubuntu，如果已知晓或者已准备好Ubuntu系统的可以跳过此节。

注意

如果C盘空间有限，在创建之前，请修改默认的Hyper-V设置中的虚拟硬盘和虚拟机的位置。

首先，我们需要打开Hyper-V管理器：

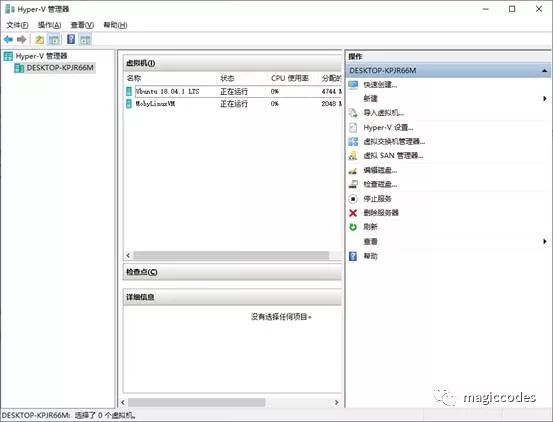
然后点击右侧的【快速创建】，并在弹出的界面中选【Ubuntu】：

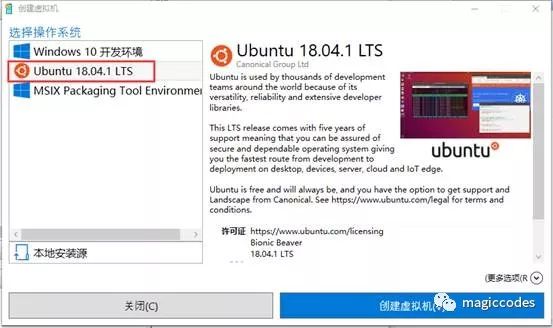
最后，点击创建虚拟机，Hyper-V管理器就会进行自动下载镜像并进行安装，如果已下载，则会从存档文件中获取并创建：

 

创建完成后如图所示：

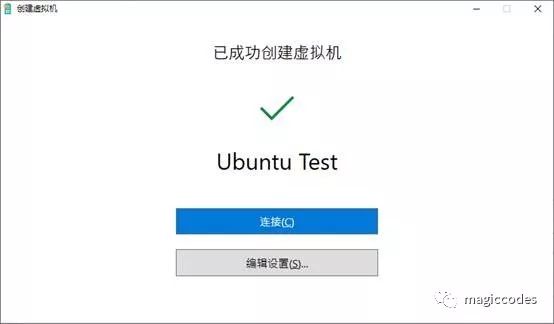
安装完成后，我们就可以连接刚安装好的Ubuntu系统了（第一次启动需要点时间）：

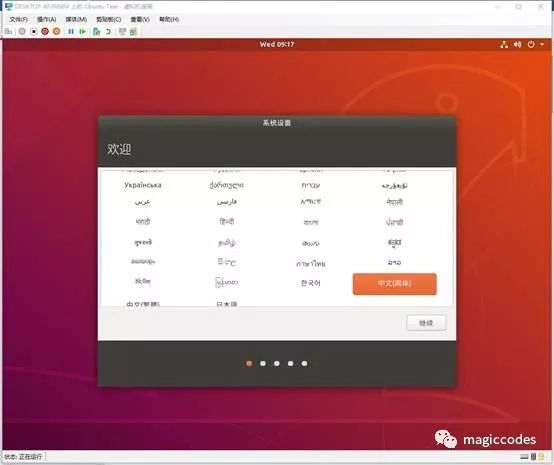
接下来就可以按照引导界面来完成系统设置，进入系统主界面了：

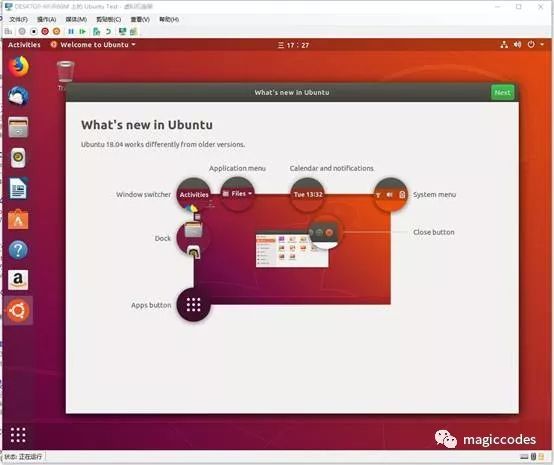
配置外网

接下来安装Docker我们需要配置外网。如果无法访问外网，我们需要配置Hyper-V的虚拟交换机。

首先，我们需要在Hyper-V管理器打开【虚拟交换机管理器】：

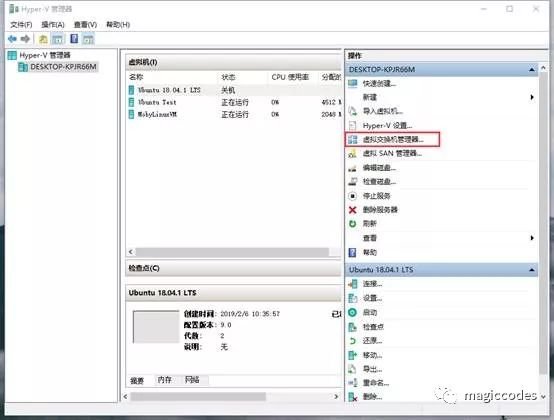
点开后，我们点击【新建虚拟网络交换机】，创建一个外部虚拟交换机：

 

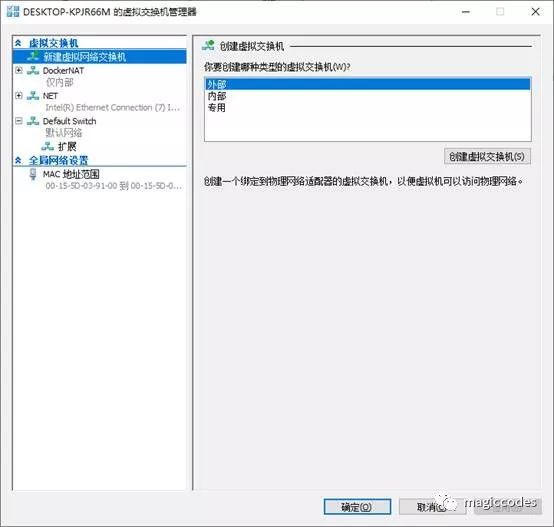
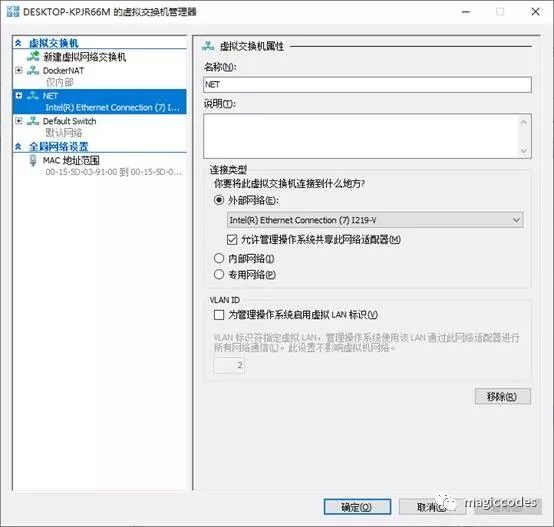
虚拟交换机创建完成后，我们需要设置虚拟机的网络适配器为刚才所创建的交换机：

 

设置完成后，我们连接并进入系统，使用自带的火狐浏览器打开百度进行确认：

使用SSH远程Ubuntu

SSH是一种网络协议，用于计算机之间的加密登录。

在Linux系统的操作上，SSH的使用是必备技能。在往后的Docker管理和操作方面，我们也离不开它。

在ubuntu上开启SSH服务

整个过程比较简单，主要分为以下步骤：

1. 进入ubuntu操作系统，打开Terminal：

2. 输入“sudo su”，切换到root账户

 

3. 安装openssh-server。

OpenSSH是Secure Shell（SSH）协议工具的免费版本，用于远程控制或在计算机之间传输文件。OpenSSH提供服务器守护程序和客户端工具，以促进安全，加密的远程控制和文件传输操作，有效地取代传统工具。

输入“apt-get install openssh-server”进行安装：

 

ssh-server配置文件位于/ etc/ssh/sshd_config，我们可以在此定义SSH的服务端口，默认端口为22。

同时，我们可以用以下命令来停止和启动SSH：

/etc/init.d/ssh stop

/etc/init.d/ssh start

如何判断ssh-server正常启动，可以使用以下命令：

ps -e |grep ssh

 

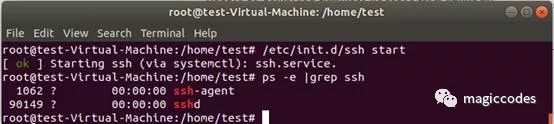
如上图所示，由于OpenSSH使用sshd来持续监听来自任何客户端工具的客户端连接，当发生连接请求时，sshd会根据连接的客户端工具的类型设置正确的连接。因此进程中存在sshd则表示正常启动。

使用SSH远程登录

这里我们使用windows 10操作系统进行演示。

1. 安装ssh客户端，这里我们使用PuTTY。因为免费。

下载地址

https://www.chiark.greenend.org.uk/~sgtatham/putty/latest.html

 

2. 接下来，我们使用账户进行SSH远程登录。

a) 获取服务端IP，可通过右上角的网络图标查看：

 

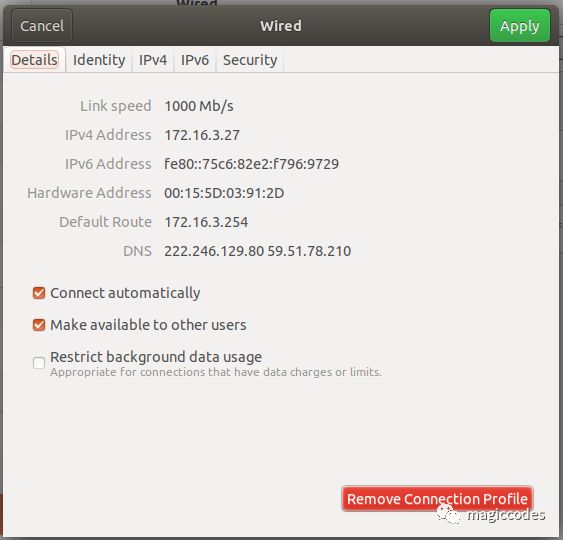
b) 打开命令窗口或者powershell窗口

 

c) 输入ssh命令进行登录。

ssh可以通过账号、公钥登录，这里我们使用账号登录：

ssh test@172.16.3.27

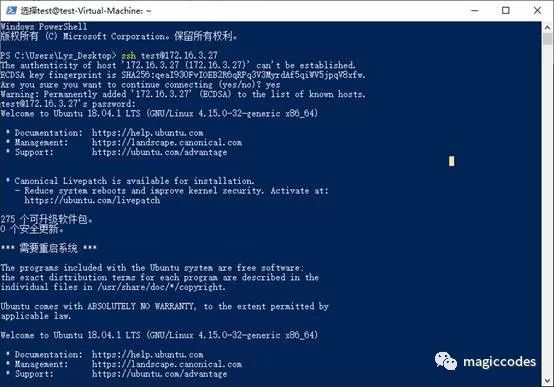如果不是使用默认端口，则需使用-p参数指定端口。登录成功之后如上图所示，注意输入密码时键盘键入内容不会有任何显示或掩码提示。连接完成后，我们真的就可以为所欲为了。比如安装Docker。

安装Docker

Docker在Linux环境下的安装推荐以下两种方式：

使用存储库安装

1. 切换到root账户（为了安装方便）

 

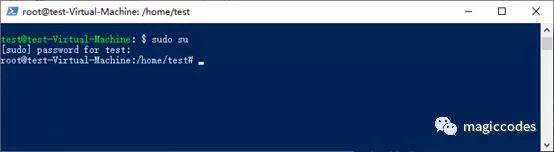
2. 更新apt包索引

apt-get update

 

3. 允许apt通过HTTPS安装

apt-get install \

    apt-transport-https \

    ca-certificates \

    curl \

    gnupg-agent \

software-properties-common

  

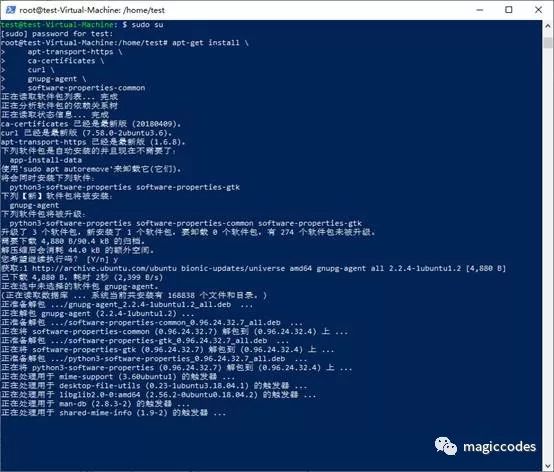
4. 添加Docker的官方GPG密钥：

curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add –

 

apt-key fingerprint 0EBFCD88

 

5. 设置稳定存储库

add-apt-repository \

   "deb [arch=amd64] https://download.docker.com/linux/ubuntu \

   $(lsb_release -cs) \

   stable"

注意

lsb_release -cs子命令返回Ubuntu发行版的名称

6. 更新apt包索引

apt-get update

 

7. 安装最新版本的Docker CE和containerd

apt-get install docker-ce docker-ce-cli containerd.io

 

注意

通过以下命令可以安装特定版本：

apt-get install docker-ce=<VERSION_STRING> docker-ce-cli=<VERSION_STRING> containerd.io

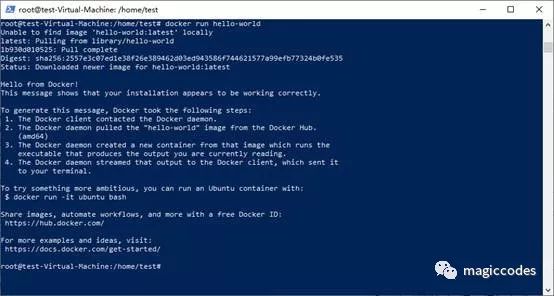
8. 按照我行行情，开始附加高级魔法，运行hello world!

docker run hello-world

 

使用快捷脚本安装

可以使用以下命令清除旧版本或者之前的安装：

apt-get remove docker-ce docker-ce-cli containerd.io docker docker-engine docker.io containerd runc

 

1. 切换到root账户（为了安装方便）

sudo su

2. 使用便捷脚本安装

Docker在get.docker.com 和test.docker.com上提供了便捷脚本，用于快速，非交互地将Docker CE的边缘和测试版本安装到开发环境中。脚本的源代码位于 docker-install存储库中。

注意

• 尽量不要在生产环境使用这些脚本
  

• 脚本需要root或sudo权限才能运行。因此，在运行脚本之前，应仔细检查和审核脚本。

• 这些脚本会尝试检测您的Linux发行版和版本，并为您配置包管理系统。此外，脚本不允许您自定义任何安装参数。

• 脚本安装包管理器的所有依赖项和建议，而不要求确认。这可能会安装大量软件包，具体取决于主机的当前配置。

• 脚本默认安装Docker的最新版本。

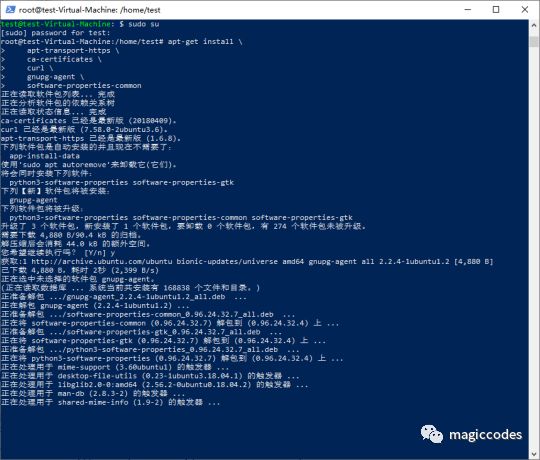
a) 允许apt通过HTTPS安装

 

apt-get install \

    apt-transport-https \

    ca-certificates \

    curl \

    gnupg-agent \

software-properties-common

 

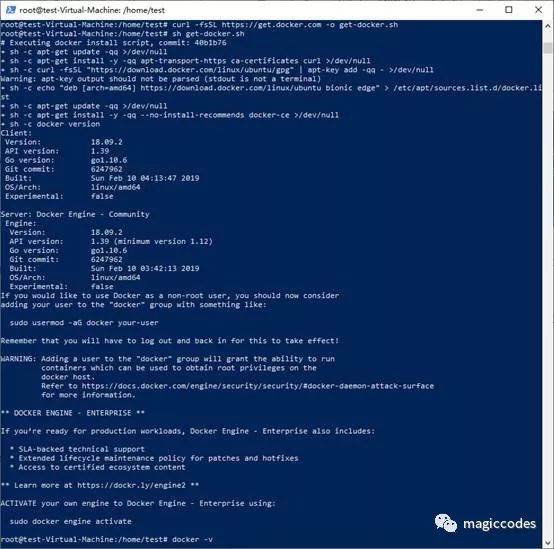
b) 下载Docker安装的便捷脚本，然后执行

curl -fsSL https://get.docker.com -o get-docker.sh

sh get-docker.sh

往期文章一览

Docker最全教程——从理论到实战（一）

Docker最全教程——从理论到实战（二）

Docker最全教程——从理论到实战（三）

Docker最全教程——从理论到实战（四）

Docker最全教程——从理论到实战（五）

Docker最全教程——从理论到实战（六）

Docker最全教程——从理论到实战（七）

Docker最全教程——从理论到实战(八)    

Docker最全教程——从理论到实战（九）

Docker最全教程之使用Tencent Hub来完成CI（十）
Docker最全教程——数据库容器化（十一）
Docker最全教程——数据库容器化之持久保存数据（十二）
Docker最全教程——MongoDB容器化（十三）
Docker最全教程——Redis容器化以及排行榜实战（十四）

转载是一种动力 分享是一种美德

如果喜欢作者的文章，请关注“magiccodes”订阅号以便第一时间获得最新内容。本文版权归作者和湖南心莱信息科技有限公司共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。

QQ群：

编程交流群<85318032> 

产品交流群<897857351>