后缀自动机：从入门到放弃

写在前面

后缀自动机，简称 $S A M$ ,是一种十分优秀的字符串匹(shu)配(ju)算(jie)法(gou)

字符串界的 $b o s s$ ，几乎可以解决全部正常的字符串题目

至少我前前后后学了一年，听过 $4$ 次课，几度怀疑自己不适合 $o i$

请做好心理准备

定义

有限状态自动机

不管，可以理解为有向图。

唯一的区别是信息储存在边上，每个点有字符集个数的转移到若干其他点，类比字典树。

如果对于一个字符串，沿着每个点的转移走，如果不出界，称该自动机可以表示这个字符串。

以下将“点”称为状态

能干啥

后缀自动机能表示母串的所有子串。

算法流程

首先明确一点：子串规模是 $O(N^2)$ 的

所以一个状态必须表示多个子串

也就是说，我们要定义出等价的子串

对于一个子串 $S$ ，定义 $e n d p o s (S)$ 为 $S$ 在原串中所有出现的结束位置的集合

每个状态与一个 $e n d p o s$ 集合一一对应。即一个状态表示一个 $e n d p o s$ 集合。

需要注意的是， $e n d p o s$ 是完全虚构的，在代码中不会出现。

然后可以表示所有 $e n d p o s$ 等于它的字符串，称这些子串为一个 $e n d p o s$ 等价类

转移

此时我们定义转移为这个类所有串加上这个字符后所在的转移。

一个类的同一个转移是相同的，因为向 $c$ 的转移的本质是当前 $e n d p o s$ 整体后移一位的所有 $c$ 的位置。

感性理解。

两个性质

1.两个子串 $S_1,S_2$ 满足 $S_1$ 是 $S_2$ 的后缀，当且仅当 $endpos(S2)⊆endpos(S1)endpos(S_2)\subseteq endpos(S_1)$

$S_2$ 出现的地方一定有 $S_1$ 出现，但有 $S_1$ 出现的地方不一定有 $S_2$

2.一个等价类中的子串均为该类中最长串的后缀且长度连续

第一个显然

对于一个串 $S$ ，若有后缀 $S_1$ 长度小于 $S$ ,且 $S_1$ 和 $S$ 是等价类

设 $S_2$ 为长度在它们之间的后缀

有 $\subseteq endpos(S_2) \subseteq endpos(S_1)$

因为 $endpos(S)=endpos(S_1)$

所以 $endpos(S) = endpos(S_2) = endpos(S_1)$

说明它们之间的串都是一个等价类

Parent链

由于类中的长度只有一段，逼死强迫症

所以我们定义每个状态 $S$ 的 $f a i l$ 指针

满足 $\in endpos(fail(S))$

且 $f a i l (S)$ 要尽量靠后

可以理解为：从一个状态沿 $f a i l$ 往上跳，取出该类中的所有串，你将会见证这个串不断失去第一个字符，不断变为后缀，最后变成空串。我们称这条链为 $p a r e n t$ 链。

先放个图，以 $A A B$ 为栗子

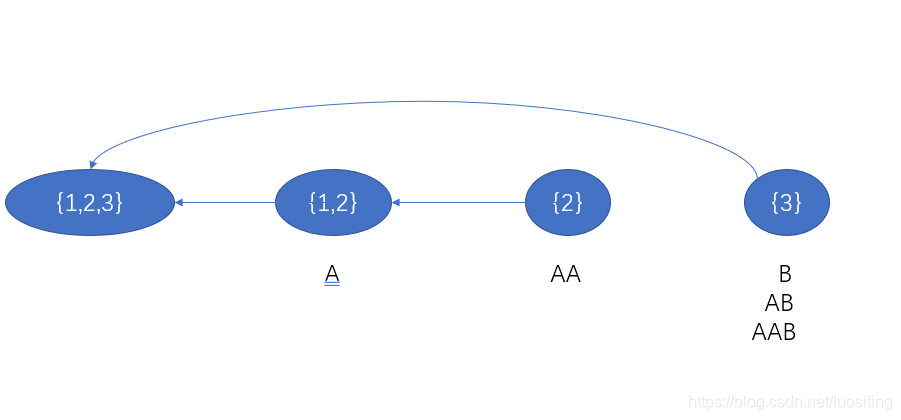
在这里插入图片描述

可能看不出啥，但有个大概印象吧

构造算法

SAM 采用增量算法，即一个一个字符插入

这使得 SAM 擅长处理动态问题

现在假设插入第 $i$ 个字符，前 $i - 1$ 个的 SAM 已经建立好

首先，上一个插入的点是整个串所在的状态，记为 $p$

新建一个节点，记为 $c u r$ 。显然 $c u r$ 最长的长度为当前串的长度。

由于其他子串已经处理了，我们要做的，就是搞出当前串的后缀

此处分 $3$ 种情况

①最简单的情况

栗子： $AA\texttt {AA}$ 插入 $B\texttt B$

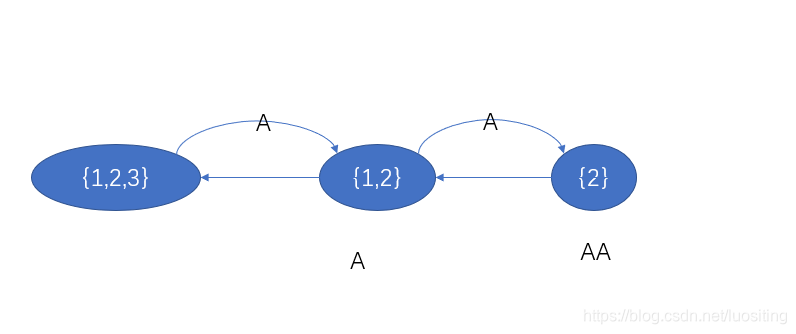
在这里插入图片描述

此时 $c u r$ 是 ${3\}$

由于每个类里的字符串是等价的（感性理解）

我们可以找到旧的串的所有后缀，给它加上新的字符

也就是让 $p$ 沿着 $f a i l$ 不断跳，令 $c h [p] [S [i]] = c u r$

即：原来的所有后缀加上新来的字符就成了新的后缀

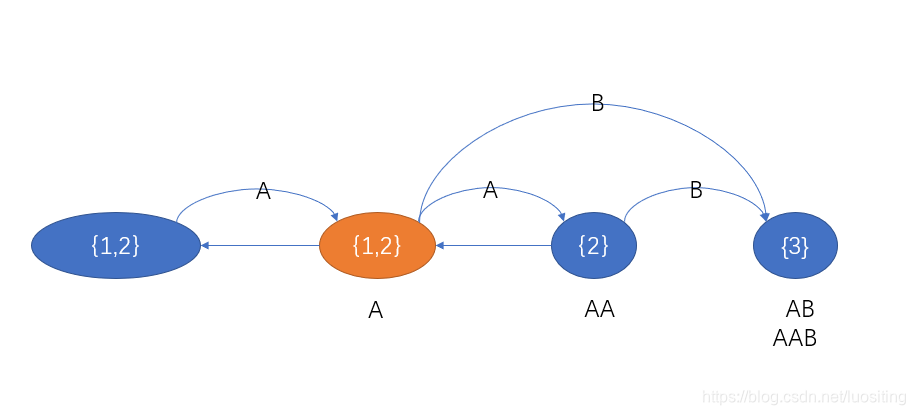
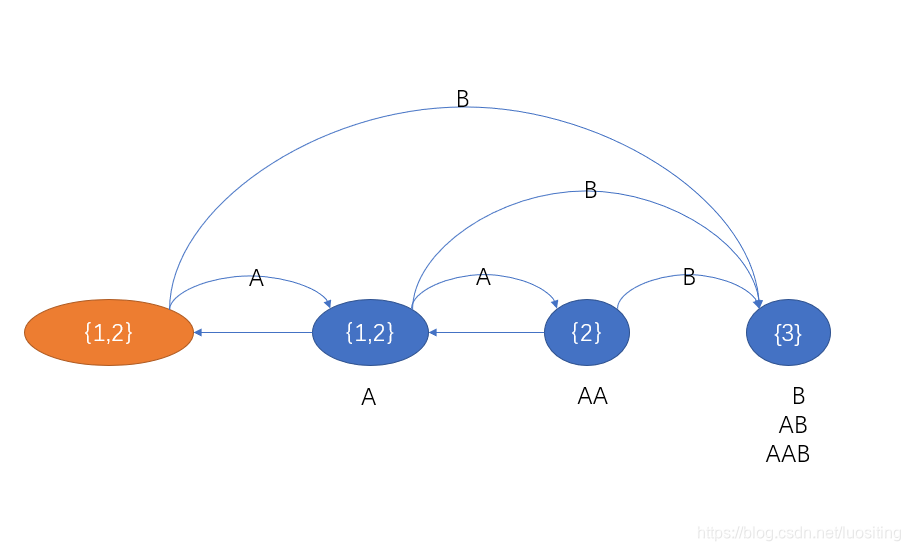
在这里插入图片描述

最后 $f a i l (c u r) = 1$ ，完结撒花

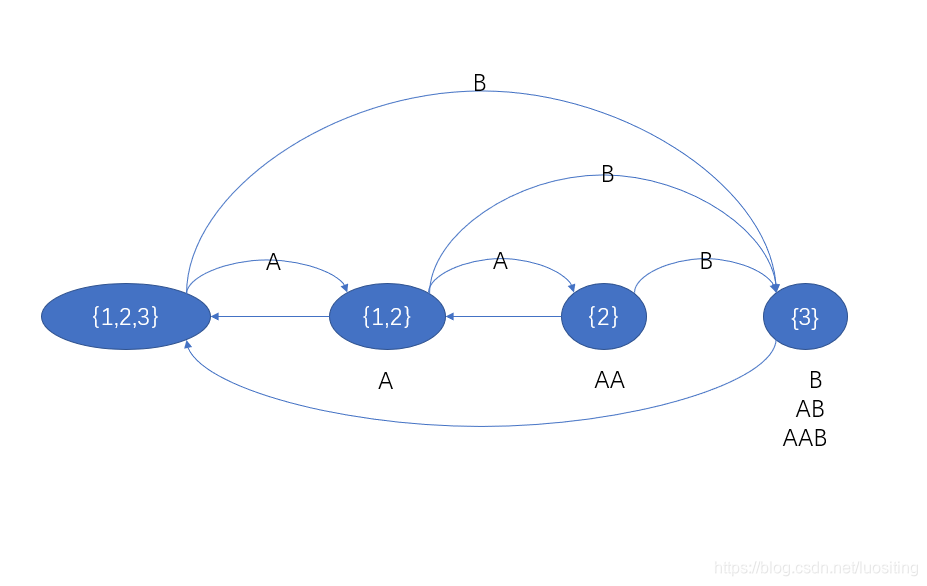
在这里插入图片描述
②然而这只是最简单的情况

栗子： $AA\texttt {AA}$ 插入 $A\texttt A$

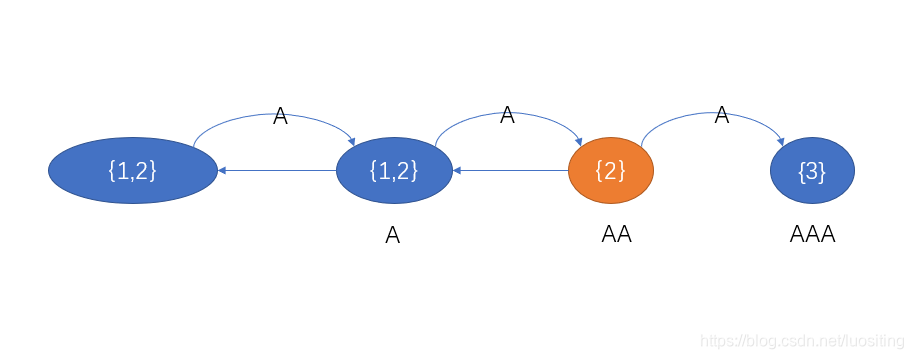
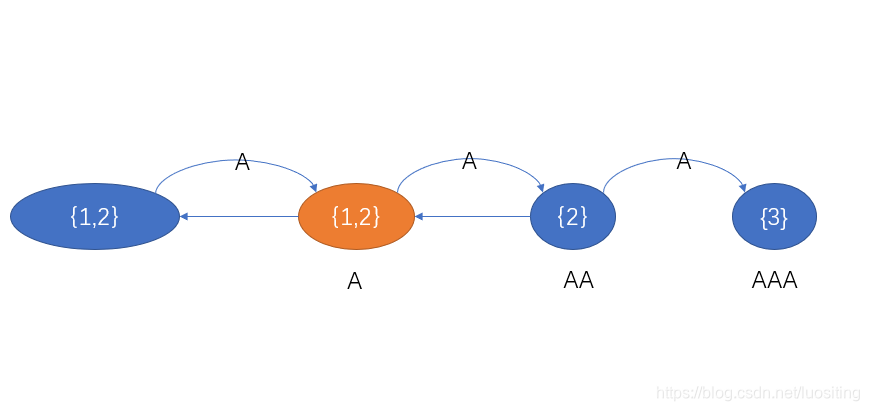
在这里插入图片描述

没区别

在这里插入图片描述
咦？已经有转移了呀

说明什么？

说明现在新串的这个后缀已经在之前的串中出现了

那这个后缀的后缀也一定出现了

（请摆脱这个栗子）

记 $q = c h [p] [S [i]]$

上面的话翻译一下， $p$ 表示的串 $+ S [i]$ 已经出现了

而这个玩意就是 $q$

……吗？

$p$ 的最长串 $+ S [i]$ 一定在 $q$ 上(定义)，但不一定是 $q$ 最长的

先讨论是最长的的情况

$y y$ 一下，我们要找的后缀不就是 $q$ 的最长串吗？

而这个后缀的后缀，也就是我们后面要找的，就在 $q$ 的 $p a r e n t$ 链上

这么说来，我们令 $f a i l [c u r] = q$ 就好了

在这里插入图片描述
over

③然而还有个最复杂的情况

也就是上面的不是 $q$ 最长的

栗子： $AAB\texttt{AAB}$ 加 $B\texttt B$

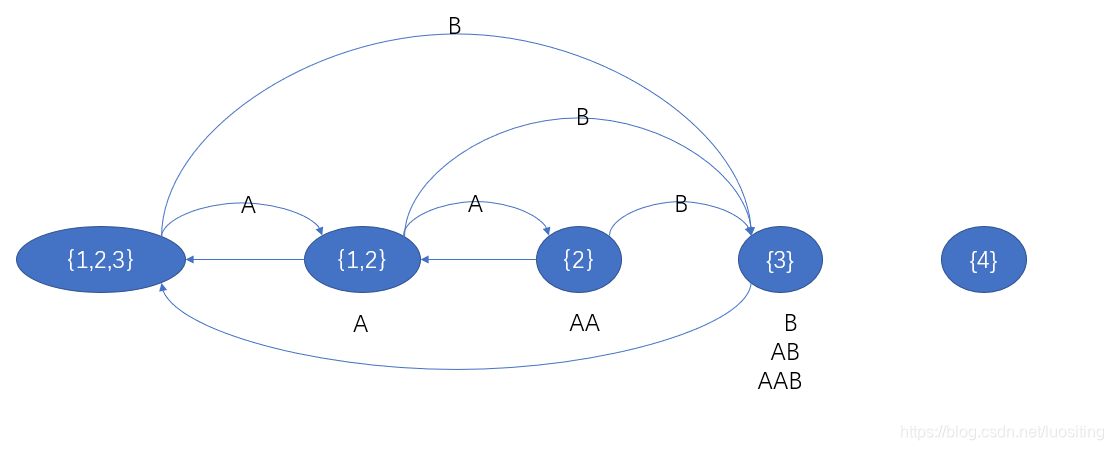
在这里插入图片描述
走程序

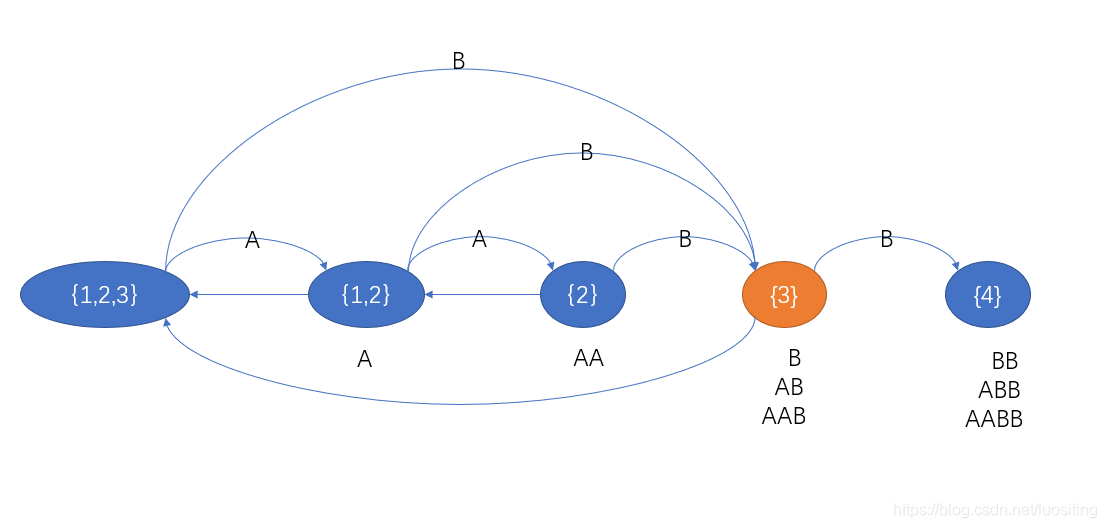
在这里插入图片描述
停

此时的 $q$ 有 $B,AB,AAB\texttt {B,AB,AAB}$

而我们的 $c u r$ 只想要 $B\texttt B$ 和链上的东西

怎么办？

拆了呗

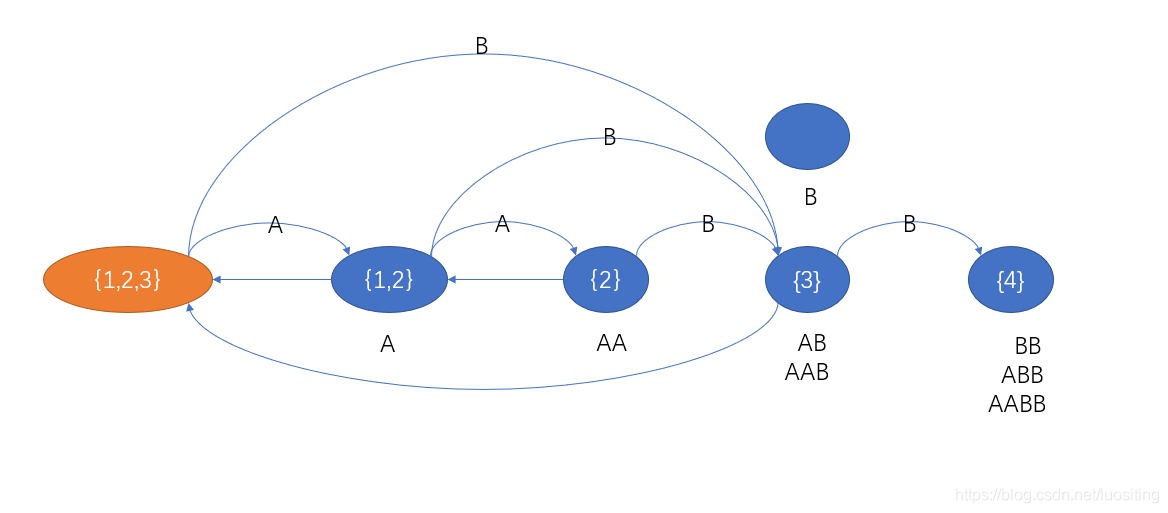
在这里插入图片描述
记新建的点为 $q^{'}$

维护信息

首先 $c u r$ 要的是 $q^{'}$ 和 $q$ 祖先上的

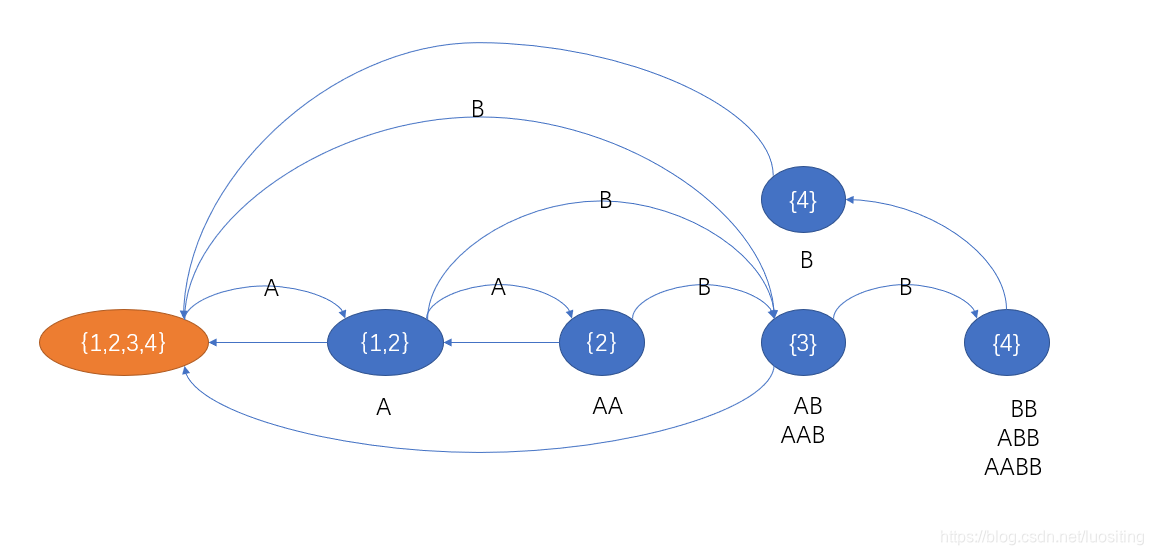
在这里插入图片描述

然后我们发现 $q$ 和 $q^{'}$ 有后缀关系

在这里插入图片描述

接下来维护转移

$q 和 q^{'}$ 是同一个分出来的，而它们原来的转移共同构成了后面的状态

现在它们拆开了，理应维护好后面

即：将 $q$ 的转移拷贝给 $q^{'}$

在这里插入图片描述

考虑这样的事实：在前面某个位置，原来转移到了这个状态。现在这个状态分了，需要考虑具体转移到哪一边。

注意到转移到 $q^{'}$ 而不转移到 $q$ ，当且仅当这个状态最长串长小于 $q^{'}$ 最长串长。

并且都是 $q$ 去掉末尾的一个字符后的后缀

~~根据意识流~~这样的状态最后面的满足的刚好是 $p$

而剩下的都在 $p$ 的 $p a r e n t$ 链上

即：跳 $p$ 的 $p a r e n t$ 链，如果有到 $q$ 的转移，将它改到 $q^{'}$

因为是后缀，所以一定是 $S [i]$ 的转移（因为 $c h [p] [S [i]] = q$ ）

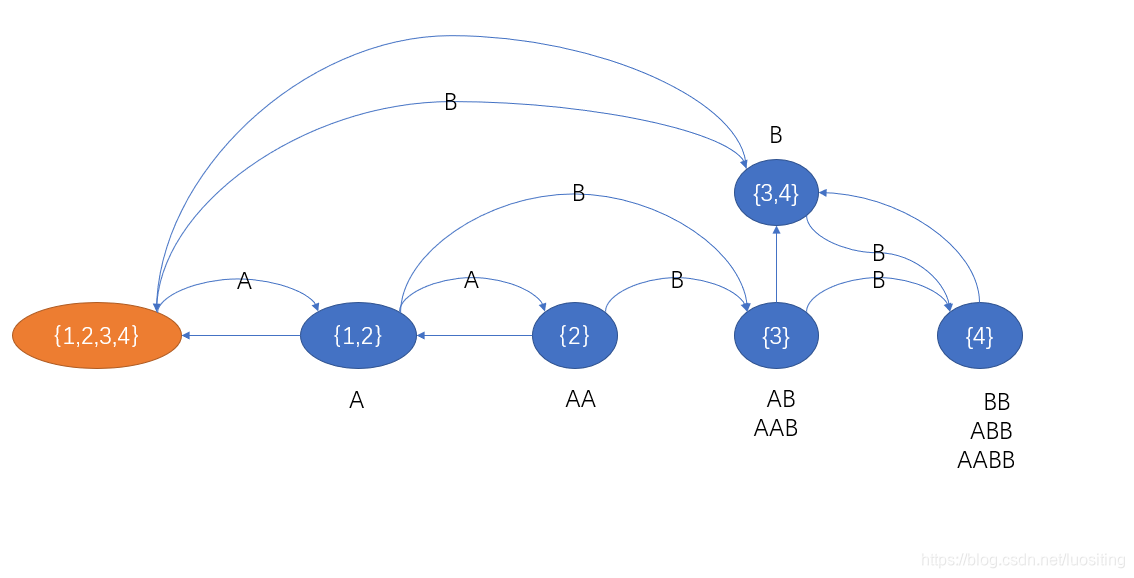在这里插入图片描述至此，SAM 就构造完毕了

复杂度是 $O (N)$ 的，显然我不会证

代码

具体实现的时候，每个节点只记录最长串的长度 $len_i$

int fa[MAXN],ch[MAXN][26];
int len[MAXN],last=1,tot=1;
int siz[MAXN],a[MAXN],c[MAXN];
void insert(int c)
{int p=last,cur=++tot;len[cur]=len[last]+1;last=cur;for (;p&&!ch[p][c];p=fa[p])  ch[p][c]=cur;//跳failif (!p) fa[cur]=1;//情况1else{int q=ch[p][c];if (len[p]+1==len[q]) fa[cur]=q;//情况2else//情况3{int clone=++tot;len[clone]=len[p]+1;for (int i=0;i<26;i++) ch[clone][i]=ch[q][i];fa[clone]=fa[q];fa[q]=fa[cur]=clone;for (;ch[p][c]==q;p=fa[p]) ch[p][c]=clone;}	}
}

运用

劈配子串

按照定义，沿着转移走

最长公共子串

建出 $S$ 的后缀自动机，拿 $T$ 去跑

不断用 $len_i$ 更新答案

如果走不动了就跳 $f a i l$

处理出现次数

对于每一次插入，一个类出现次数增加，当且仅当这是当前的后缀

也就是把这个点的 $p a r e n t$ 链都 $+ 1$

显然会 $T$ 。于是先建完，按长度瞎排个序，倒着往上推。

这样 $siz_i$ 表示状态 $i$ 中的一个串的出现次数。显然它们是一样的。

应该是用的最多的。

void query()
{for (int i=1;i<=tot;i++) c[len[i]]++;for (int i=1;i<=n;i++) c[i]+=c[i-1];for (int i=1;i<=tot;i++) a[c[len[i]]--]=i;for (int i=tot;i>=1;i--) siz[fa[p]]+=siz[p];
}