传送门
文章目录
- 题意:
- 思路:
题意:
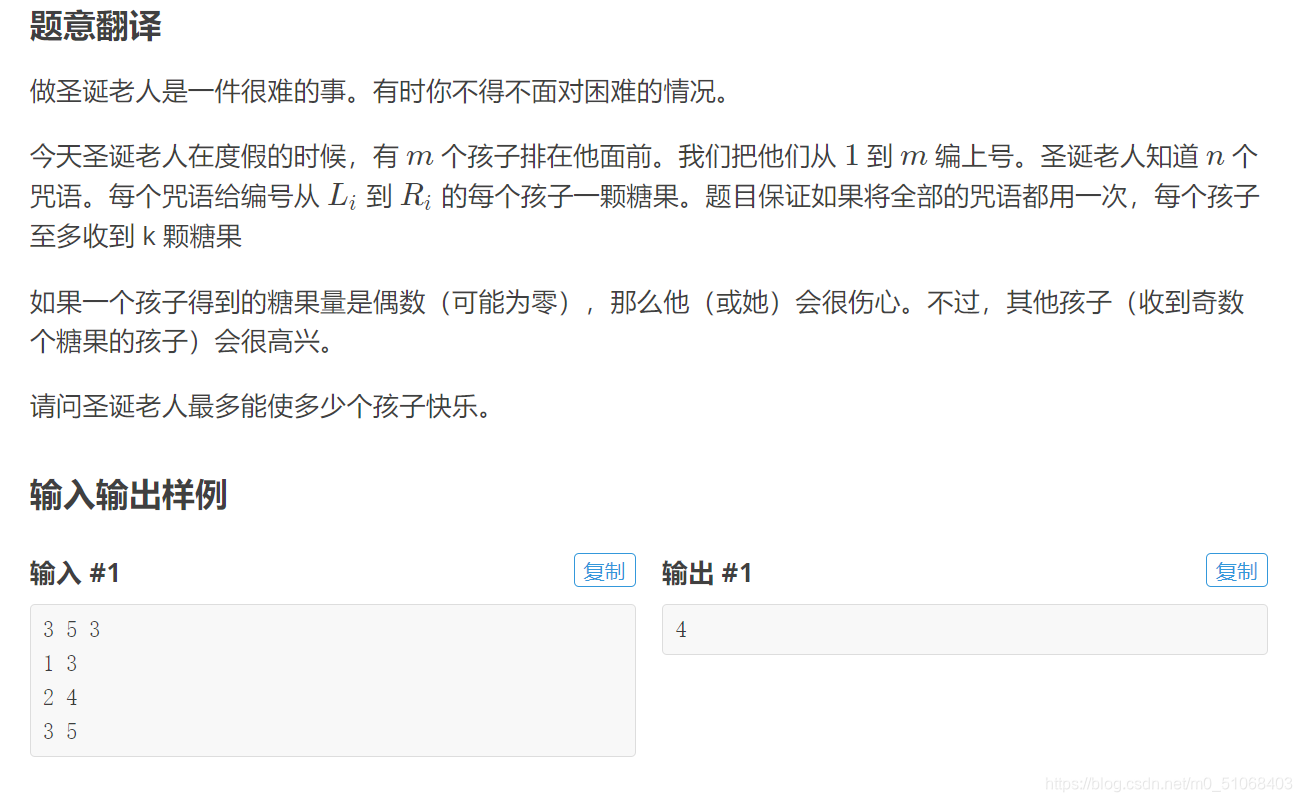
n≤1e5,m≤1e9,k≤8.n\le 1e5,m\le 1e9,k\le 8.n≤1e5,m≤1e9,k≤8.
思路:
注意到题目中保证了每个孩子至多收到kkk个,且k≤8k\le 8k≤8,注意到这是题目保证的,并不是说这个孩子能收到很多,但是收到kkk个就接受不了别的了,我理解错题意想了一晚上。
看到kkk这么小,自然的想到状压了,复杂度O(n∗2k)O(n*2^k)O(n∗2k)很完美。
发现区间很大,自然想到离散化。通过离散化, 我们可以将其分成若干个左闭右开的区间。这个时候就可以定义f[i][j]f[i][j]f[i][j]表示选到了第iii个区间,且该区间的状态为jjj。jjj是一个长度为kkk的二进制,某一位iii是111表示第iii条线覆盖了这个区间。由于区间是左闭右开的区间,所以左端点才有信息存储,下面分情况讨论:
设当前状态为jjj,其含有的111的个数为cntcntcnt,当前这段区间在第kkk个。
当前需要加上一段区间:
(1)(1)(1)如果jjj的第k−1k-1k−1位已经存在,那么应该从前一个状态不含这一位转移过来,即 f[i][j]=f[i−1][jxor1<<k]+len∗(cntmod2)f[i][j]=f[i-1][j \ \ xor \ \ 1<<k]+len*(cnt\bmod 2)f[i][j]=f[i−1][j xor 1<<k]+len∗(cntmod2)
(2)(2)(2)如果jjj的第k−1k-1k−1位不存在,那么应该从上一个jjj的状态转移,即f[i][j]=f[i−1][j]+len∗(cntmod2)f[i][j]=f[i-1][j]+len*(cnt\bmod 2)f[i][j]=f[i−1][j]+len∗(cntmod2)
当前需要减去一段区间:
(1)(1)(1)如果jjj的k−1k-1k−1位已经存在,由于我们是要删掉他,所以应该将他置为−INF-INF−INF,即f[i][j]=−INFf[i][j]=-INFf[i][j]=−INF。
(2)(2)(2)如果jjj的k−1k-1k−1位不存在,那么从上一个状态的jjj或jxor1<<kj\ \ xor\ \ 1<<kj xor 1<<k二者大的一个转移过来,再加上len∗(cntmod2)len*(cnt\bmod 2)len∗(cntmod2)即可,即f[i][j]=max(f[i−1][j],f[i−1][jxor1<<k])+len∗(cntmod2)f[i][j]=max(f[i-1][j],f[i-1][j \ \ xor \ \ 1<<k])+len*(cnt\bmod 2)f[i][j]=max(f[i−1][j],f[i−1][j xor 1<<k])+len∗(cntmod2)。
第一维直接滚动一下就好了,或者直接开一维,让后注意一下遍历的顺序就好啦,具体看代码吧。
// Problem: D. Happy New Year
// Contest: Codeforces - Codeforces Round #622 (Div. 2)
// URL: https://codeforces.com/contest/1313/problem/D
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)//#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")
//#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<cctype>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
#include<sstream>
#include<ctime>
#include<cstdlib>
#define X first
#define Y second
#define L (u<<1)
#define R (u<<1|1)
#define pb push_back
#define mk make_pair
#define Mid (tr[u].l+tr[u].r>>1)
#define Len(u) (tr[u].r-tr[u].l+1)
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define db puts("---")
using namespace std;//void rd_cre() { freopen("d://dp//data.txt","w",stdout); srand(time(NULL)); }
//void rd_ac() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//AC.txt","w",stdout); }
//void rd_wa() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//WA.txt","w",stdout); }typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;const int N=400010,mod=1e9+7,INF=0x3f3f3f3f;
const double eps=1e-6;int n,m,k;
PII p[N];
vector<int>v;
int st[N];
LL f[2][(1<<8)+10];int find(int x)
{return lower_bound(v.begin(),v.end(),x)-v.begin();
}int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);int tot=0,op=0;scanf("%d%d%d",&n,&m,&k);for(int i=1;i<=n;i++){int l,r; scanf("%d%d",&l,&r);v.pb(l); v.pb(r+1);p[++tot]={l,i}; p[++tot]={r+1,-i};}//for(int i=1;i<(1<<k);i++) f[0][i]=-INF;memset(f,-0x3f,sizeof(f));f[op][0]=0;sort(p+1,p+1+tot);LL ans=0;for(int i=1;i<=tot;i++) {op^=1;int len=p[i+1].X-p[i].X;if(i==tot) len=0;int id=p[i].Y,pos;if(id>0) {for(int j=0;j<k;j++) if(st[j]==0) { pos=j; st[j]=id; break; }for(int j=0;j<(1<<k);j++)if(j>>pos&1) f[op][j]=f[op^1][j^1<<pos]+len*__builtin_parity(j);else f[op][j]=f[op^1][j]+len*__builtin_parity(j);}else {for(int j=0;j<k;j++) if(st[j]==-id) { pos=j; st[j]=0; break; }for(int j=0;j<(1<<k);j++)if(j>>pos&1) f[op][j]=-INF;else f[op][j]=max(f[op^1][j],f[op^1][j^1<<pos])+len*__builtin_parity(j);}}cout<<f[op][0]<<endl;/*for(int i=1;i<=tot;i++){int len;if(i!=tot) len=p[i+1].X-p[i].X;else len=0;int id=p[i].Y,pos;if(id>0){for(int i=0;i<k;i++) if(st[i]==0) { pos=i; st[i]=id; break; }for(int i=(1<<k)-1;i>=0;i--) if(i>>pos&1) f[i]=f[i^1<<pos]+len*__builtin_parity(i);else f[i]=f[i]+len*__builtin_parity(i);}else {for(int i=0;i<k;i++) if(st[i]==-id) { pos=i; st[i]=0; break; }for(int i=0;i<(1<<k);i++) if(i>>pos&1) f[i]=INF;else f[i]=max(f[i],f[i^1<<pos])+len*__builtin_parity(i);}} printf("%lld\n",f[0]);*/return 0;
}
/**/

 D. Three Integers 数论)




 E. Construct the Binary Tree 思维 + 构造)




E. The Three Little Pigs-长除法求多项式系数)

 C. Continuous City 构造 + 二进制)




