https://ac.nowcoder.com/acm/contest/11255/E
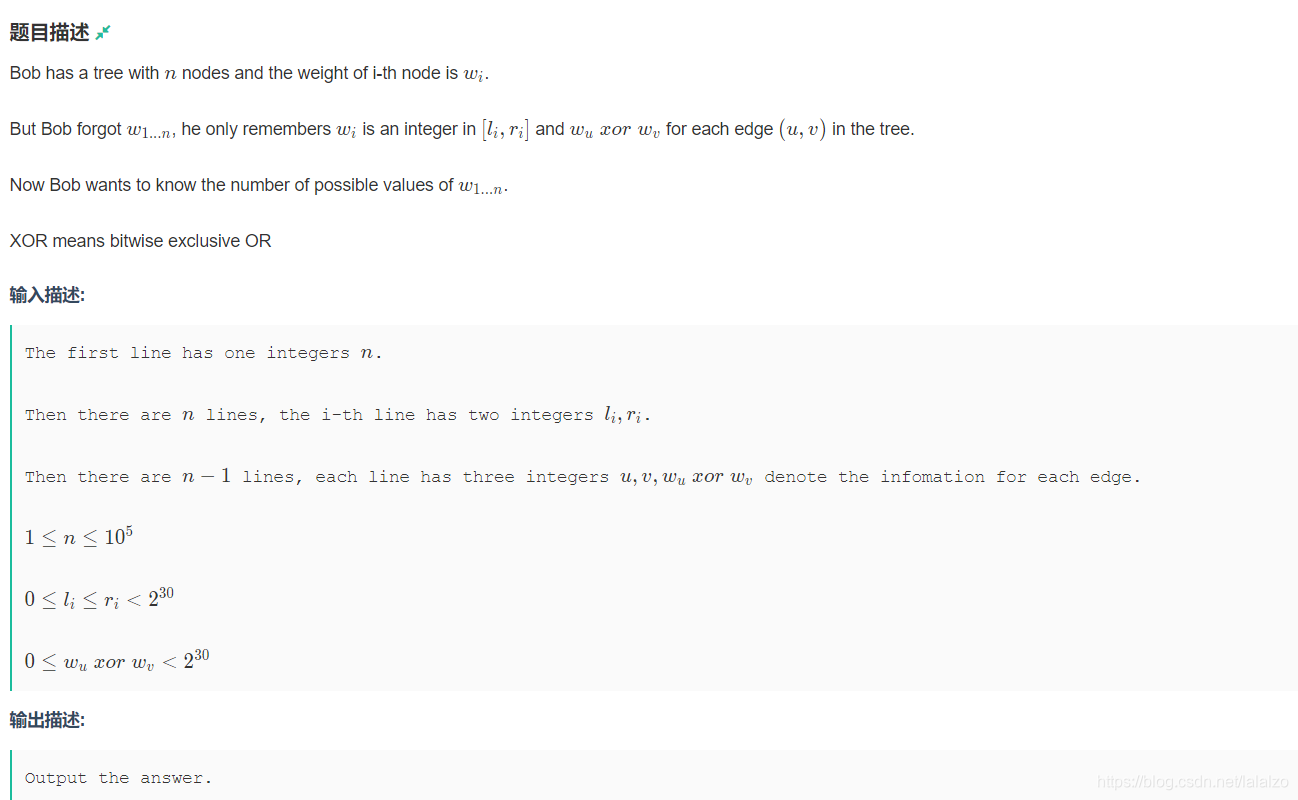
题目大意：有n个点，每一点有一个区间[l,r]范围的权值可能，有n-1条边，边上的权值为w,w=w(u)^w(v),问你满足权值范围和边权值的方案数。
思路：我们把树根的值设为0，这样其他点的w值也随之确定，然后树根的值变为a，那么其他点的值也会变为w^a。根据这个性质，那我们只要求出a的范围就好了，即所有的区间异或对应的w值，就可以求出a的范围，再求出所有点a的范围的交集。对于区间异或上w值，我们可以使用线段树。
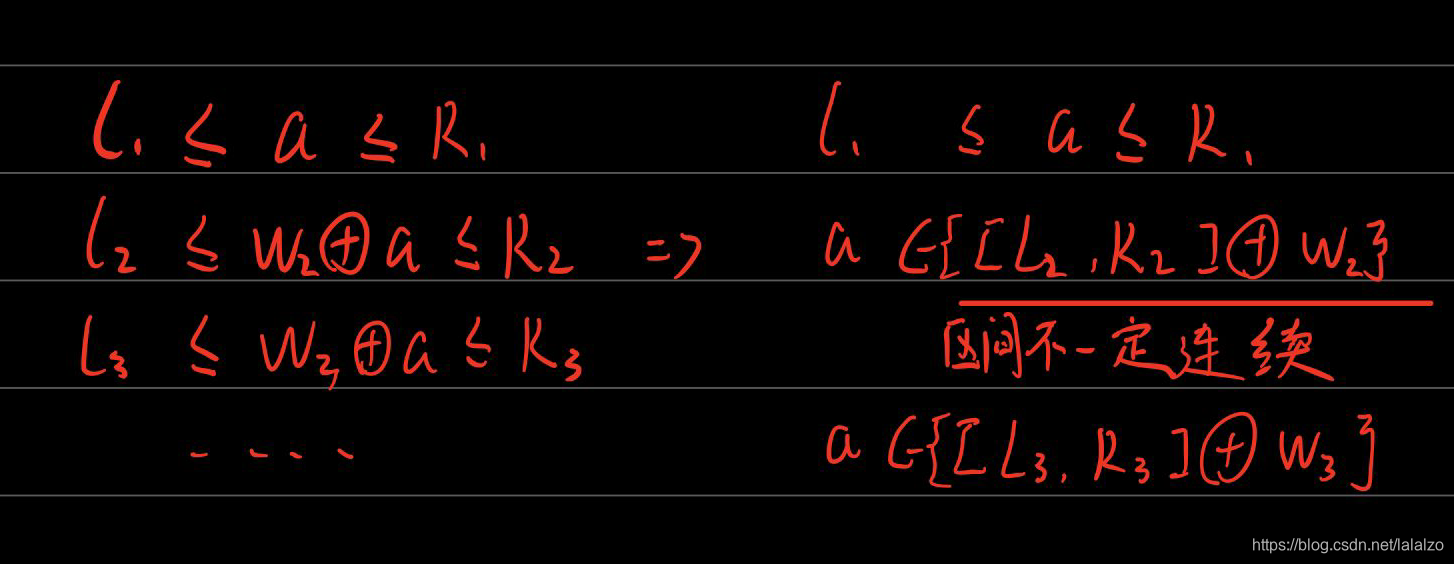
我们将利用线段树 将不连续的区间分为logw段连续的区间。
做法一：n*logn 使用线段树可以求出所有不合法区间的并集，把不合法的区间标记为1，可以没有标记过的区间说明对于这n个点这些区间都是合法的。
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cstdlib>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <bitset>
#include <complex>
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define FILL(a,b) (memset(a,b,sizeof(a)))
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(a) ((a)&-(a))
#define ios std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
#define fi first
#define sc second
#define pb push_back
#define all(x) (x).begin(),(x).end()
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll,ll> pii;
const ll mod=1e9+7;
const ll N =6e6+10;
const double eps = 1e-6;
const double PI=acos(-1);
ll gcd(ll a,ll b){return !b?a:gcd(b,a%b);}
ll re(){ll x;scanf("%lld",&x);return x;}
int dx[8]= {1,0,-1,0,1,1,-1,-1}, dy[8] = {0,1,0,-1,1,-1,1,-1};
int n;
int ch[N][2],sum[N];
bool tag[N];
vector<pii> g[N];
int l[N],r[N];
int cnt=1,root=1;
void add(int &rt,int l,int r,int x,int y,int w){int len=r-l+1;int l1=l^(w&(~(len-1)));// ~(len-1)代表求出类11000000的格式，再将w前面的几位屏蔽掉，在和L异或，就是他们的起点了。int r1=l1+len-1;//l-r这个区间可以由l1-r1这个区间异或w得到if(l1>=x&&r1<=y) return;if(!rt) rt=++cnt;//动态开点if(l1>y||r1<x){//将其他区间的值设为1；tag[rt]=1;//标记该区间都是不合法的；sum[rt]=len;return;}if(tag[rt]) return;int mid=(l+r)/2;add(ch[rt][0],l,mid,x,y,w);add(ch[rt][1],mid+1,r,x,y,w);if(tag[rt]) sum[rt]=len;else sum[rt]=sum[ch[rt][0]]+sum[ch[rt][1]];
}
void dfs(int u,int f,int w){add(root,0,(1<<30)-1,l[u],r[u],w);for(pii v:g[u]){if(v.fi==f) continue;dfs(v.fi,u,w^(v.sc));}
}
void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>l[i]>>r[i];for(int i=1;i<n;i++){int u,v,w;cin>>u>>v>>w;g[u].pb({v,w});g[v].pb({u,w});}dfs(1,0,0);cout<<(1<<30)-sum[1]<<"\n";
}int main()
{iosint T=1;while(T--){solve();}return 0;
}做法二：n*logn*logn直接用线段求出所有合法区间，最后再利用差分求区间并，区间并==n时，该段区间合法。
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cstdlib>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <bitset>
#include <complex>
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define FILL(a,b) (memset(a,b,sizeof(a)))
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(a) ((a)&-(a))
#define ios std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
#define fi first
#define sc second
#define pb push_back
#define all(x) (x).begin(),(x).end()
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll,ll> pii;
const ll mod=1e9+7;
const ll N =1e6+10;
const double eps = 1e-6;
const double PI=acos(-1);
ll gcd(ll a,ll b){return !b?a:gcd(b,a%b);}
ll re(){ll x;scanf("%lld",&x);return x;}
int dx[8]= {1,0,-1,0,1,1,-1,-1}, dy[8] = {0,1,0,-1,1,-1,1,-1};
int n;
vector<pii> g[N];
vector<pii> ans;
int l[N],r[N];void gao(int l,int r,int w){int len=r-l+1;int l1=l^(w&~(len-1));ans.pb({l1,l1+len-1});
}
void add(int l,int r,int x,int y,int w){//线段树if(x<=l&&r<=y){gao(l,r,w);return;}int mid=(l+r)>>1;if(x<=mid) add(l,mid,x,y,w);if(y>mid) add(mid+1,r,x,y,w);
}
void dfs(int u,int f,int w){add(0,(1<<30)-1,l[u],r[u],w);for(pii v:g[u]){if(v.fi==f) continue;dfs(v.fi,u,w^v.sc);}
}void gg(){vector<pii> dp;for(pii v:ans){dp.pb({v.fi,1});dp.pb({v.sc+1,-1});}sort(all(dp));int sum=0;int ans=0;for(int i=0;i<dp.size();i++){pii v=dp[i];sum+=v.sc;if(sum>=n) ans+=dp[i+1].fi-v.fi;}cout<<ans<<endl;
}
void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>l[i]>>r[i];for(int i=1;i<n;i++){int u,v,w;cin>>u>>v>>w;g[u].pb({v,w});g[v].pb({u,w});}dfs(1,0,0);gg();
}
int main()
{iosint T=1;while(T--){solve();}return 0;
}
看到群上说用trie树也可以写，就去学习了一下，一样的把不合法的标记了，最后求出没有标记过的点数量就是答案（代码有注释了）
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cstdlib>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <bitset>
#include <complex>
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define FILL(a,b) (memset(a,b,sizeof(a)))
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(a) ((a)&-(a))
#define ios std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
#define fi first
#define sc second
#define pb push_back
#define all(x) (x).begin(),(x).end()
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll,ll> pii;
const ll mod=1e9+7;
const ll N =6e6+10;
const double eps = 1e-6;
const double PI=acos(-1);
ll gcd(ll a,ll b){return !b?a:gcd(b,a%b);}
ll re(){ll x;scanf("%lld",&x);return x;}
int dx[8]= {1,0,-1,0,1,1,-1,-1}, dy[8] = {0,1,0,-1,1,-1,1,-1};int n;
vector<pii> g[N];
int l[N],r[N];
int tag[N],ch[N][2],cnt;
ll ans;
int newnode(){cnt++;tag[cnt]=ch[cnt][0]=ch[cnt][1]=0;return cnt;
}
int add(int x,int f,int l,int r,int w){if(tag[x]==2){//tag=2表示01两科子树下都没有答案return tag[x];}if((r-l)==((1<<(f+1))-1)){//出现00000000~11111111的情况时，因为在这个子树下现在w的所以答案都是合法的，无论怎么异或都是在这个子树的，所以保持该子树的状态return tag[x];}if(!ch[x][0]) ch[x][0]=newnode();//动态开点if(!ch[x][1]) ch[x][1]=newnode();if((l&(1<<f))==(r&(1<<f))){//第f位相同的情况下int id=(((l&(1<<f))^(w&(1<<f)))!=0);//求出第f位的状态，因为第f位相同，所以只有一种状态tag[ch[x][!id]]=2;//！id的这个子树所有答案都是不合法的int k=add(ch[x][id],f-1,l%(1<<f),r%(1<<f),w);//遍历到下一个子树if(k==2) tag[x]=2;else tag[x]=1;}else{//第f位不同的情况下int id=((w&(1<<f))!=0);//观察w的f位情况//分割区间 第f位为0和为1的情况int k1=add(ch[x][id],f-1,l%(1<<f),(1<<f)-1,w);//第f位是0的情况下int k2=add(ch[x][!id],f-1,0,r%(1<<f),w);//第f位是1的情况下if(k1==2&&k2==2)tag[x]=2;else if(k1!=2||k2!=2) tag[x]=1;}return tag[x];
}
void dfs(int u,int f,int w){add(1,29,l[u],r[u],w);for(pii v:g[u]){if(v.fi==f) continue;dfs(v.fi,u,w^v.sc);}
}
void gg(int x,int f){if(tag[x]==0){//该子树下的答案全部是合法的ans+=(1ll<<(f+1));}else if(tag[x]==1){if(tag[ch[x][1]]!=2) gg(ch[x][1],f-1);if(tag[ch[x][0]]!=2) gg(ch[x][0],f-1);}
}
void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>l[i]>>r[i];for(int i=1;i<n;i++){int u,v,w;cin>>u>>v>>w;g[u].pb({v,w});g[v].pb({u,w});}newnode();dfs(1,0,0);gg(1,29);//递归计算统计答案cout<<ans<<endl;
}
int main()
{iosint T=1;while(T--){solve();}return 0;
}
