Apollo(阿波罗)是携程框架部门研发的分布式配置中心,能够集中化管理应用不同环境、不同集群的配置,配置修改后能够实时推送到应用端,并且具备规范的权限、流程治理等特性,适用于微服务配置管理场景。
服务端架构
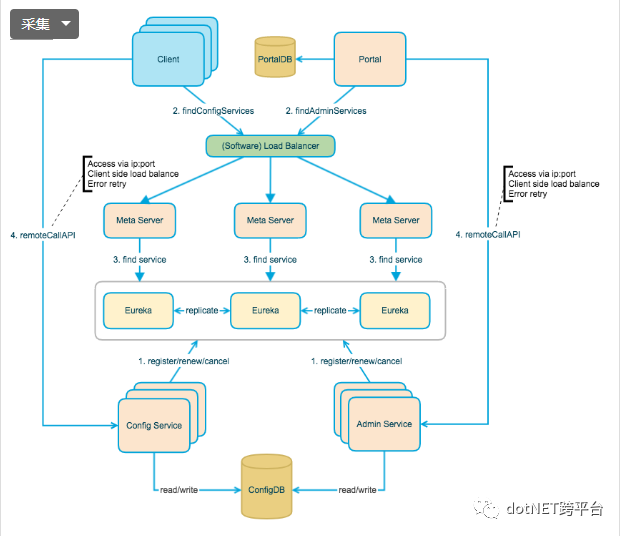
上图简要描述了 Apollo 的总体设计:
Config Service 提供配置的读取、推送等功能,服务对象是 Apollo 客户端
Admin Service 提供配置的修改、发布等功能,服务对象是 Apollo Portal(管理界面)
Config Service 和 Admin Service 在生产环境都是多实例、无状态部署,所以需要将自己注册到 Eureka 中并保持心跳
在 Eureka 之上有一层 Meta Server 用于封装 Eureka 的服务发现接口
Client 通过域名访问 Meta Server 获取 Config Service 服务列表(IP+Port),而后直接通过 IP+Port 访问服务,同时在 Client 侧会做 load balance、错误重试
Portal 通过域名访问 Meta Server 获取 Admin Service 服务列表 IP+Port,而后直接通过 IP+Port 访问服务,同时在 Portal 侧会做 load balance、错误重试
部署策略
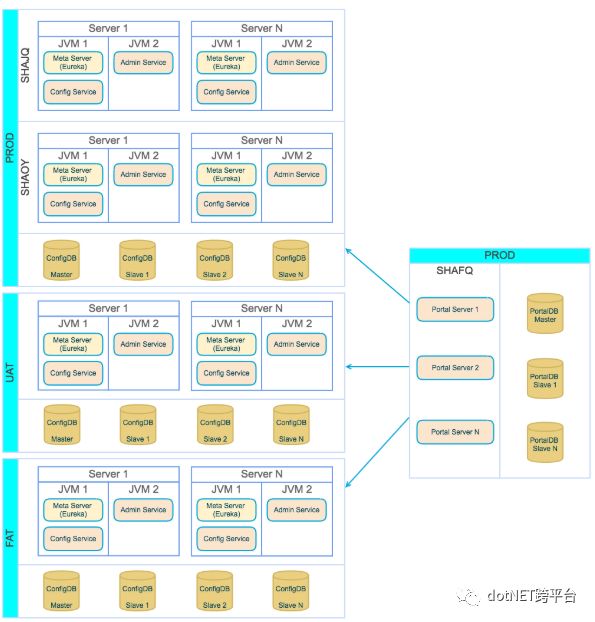
上图描述了 Apollo 的部署策略:
PortalDB 主要保存权限、支持的环境等数据,Apollo Portal 环境只需要部署一套,管理所有环境(DEV、FAT、UAT、PRO)
ConfigDB 保存应用相关的配置数据,每个环境需要独立的 ConfigDB 数据库
为保证稳定性,PortalDB 和 ConfigDB 需要支持 Master-Slave 模式
为简化部署,实际上会把 Config Service、Eureka 和 Meta Server 部署在同一个 JVM 进程中,Admin Service 部署在另一个 JVM 线程中
Meta Server、Eureka 、Config Service 和 Admin Service 在生产环境可部署在两个机房,实现双活
客户端架构
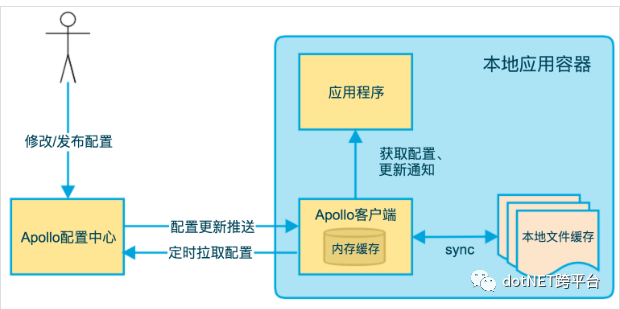
上图简要描述了 Apollo 客户端的实现原理:
客户端和服务端保持了一个长连接,从而能第一时间获得配置更新的推送
客户端会定时从 Apollo 配置中心服务端拉取应用的最新配置(防止推送机制失效导致配置不更新)
客户端从 Apollo 配置中心服务端获取到应用的最新配置后,会保存在内存中
客户端会把从服务端获取到的配置在本地文件系统缓存一份,在遇到服务不可用,或网络不通的时候,依然能从本地恢复配置
应用程序从 Apollo 客户端获取最新的配置、订阅配置更新通知
分布式部署
通过以上的介绍,可以看出 Apollo 的整体架构并不简单,但其实也不用担心,在部署上也并没那么复杂。接下来主要介绍 Apollo 的分布式部署,之后的文章中会介绍如何在 Java、.NET 客户端中使用,部署将使用 Docker 的方式,所以读者最好有一定的 Docker 基础。
有 Apollo 用户已经提供了现成的 Dcoker 镜像 ,我们可以直接使用。不过这里还是将通过编译源代码的方式来介绍,目的是从最原始操作开始,了解整个过程的实现。
环境要求
JDK 1.8+ (安装后,修改 Path 环境变量)
Maven 3.5+ (安装后,修改 Path 环境变量,建议修改 Maven 源地址,加快下载速度)
MySQL 5.6.5+
Docker
JDK 和 Maven 只在编译 Apollo 源代码时使用,实际使用 Docker 部署并不需要。
创建数据库
从部署策略图中可以看出,搭建 Apollo 环境需要使用到 PortalDB、ConfigDB 两个数据库,这两个数据库的初始脚本官方源码中已提供:
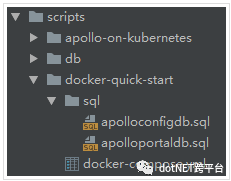
我们需要在自己的数据库上执行以上两个文件的脚本,这里将搭建一个基于 PRO 的分布式环境( 如果需要支持多个环境,需要在对应环境的数据库上建 ConfigDB,服务启动改成对应环境的数据库连接,更多请参考 调整ApolloPortalDB配置 和 调整ApolloConfigDB配置 ),如下:

构建 Docker 镜像
下载最新 apollo master 分支 代码(当前是 1.5.0-SNAPSHOT),网上很多介绍都需要修改源代码后再进行编译,这个版本已有哥们提交了 Merge Request ,使在 Docker 部署上更简化了。如有特殊需要,也可自行修改源码。
下载完成后在根目录下执行
.\scripts\build.bat(我是在 windows 进行编译的),编译成功后在apollo-adminservice、apollo-configservice、apollo-portal下的 target 目录会生成对应压缩包pollo-configservice-1.5.0-SNAPSHOT-github.zip、apollo-adminservice-1.5.0-SNAPSHOT-github.zip、apollo-portal-1.5.0-SNAPSHOT-github.zip,这个几个文件就是我们在构建 Docker 镜像需要的Apollo源码中已经提供了构建 Docker 镜像的 Dockerfile 文件,
apollo-configservice\src\main\docker\Dockfile、apollo-adminservice\src\main\docker\Dockfile、apollo-portal\src\main\docker\Dockfile可以直接使用,最终如下:
分别构建 Docker 镜像,然后可以通过 docker push 推送到自己的 Docker 仓库,比如 我的仓库 ,或者在要部署是机器上生成 Docker 镜像直接使用,最终得到
apollo-configservice、apollo-adminservice、apollo-portal3个镜像。

编写 docker-compose
apollo-configservice && apollo-adminservice:
apollo-portal:
初始数据库数据修改
ApolloPortalDB 库的 ServerConfig 表 apollo.portal.envs 和 configView.memberOnly.envs值修改为:pro;(因为这里我们搭建的是 PRO 的分布式环境)
ApolloConfigDB 库的 ServerConfig 表 eureka.service.url 值修改为:http://${实例1的 apollo-configservice 地址}/eureka/,http://${实例2的 apollo-configservice 地址}/eureka/;
启动服务
这里将在同一个机器上启动 1 个 apollo-portal 实例(端口 8070),2 个 apollo-configservice(端口 8080、8081)和 2 个 apollo-adminservice(端口 8090、8091)。
注意:启动的过程会比较慢,一般会在 100~200s 左右

通过访问 http://${apollo-portal 服务IP}:8070 ,输入默认用户名密码 apollo/admin 登录:(当前的测试脚本提供一个默认的测试项目,新版本的 sql 脚本可能没有 SampleApp)
通过 管理员工具 => 系统信息 可查看当前环境信息:
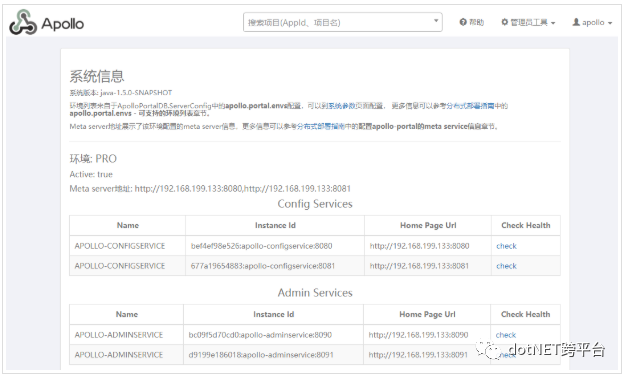
可以看出 Config Services 和 Admin Services 都是两个实例,我们可以模拟 kill 其中一台,服务依然是可以正常使用的。
接下来就可以创建应用,添加配置信息,提供给客户端使用,具体客户端如何使用后续将会继续介绍。
参考链接
Apollo
Apollo 分布式部署指南




 New Equipments(最小费用最大流))


![[CQOI2007]涂色PAINT](http://pic.xiahunao.cn/[CQOI2007]涂色PAINT)







C generator 2 (BSGS))


![P2303 [SDOI2012] Longge 的问题](http://pic.xiahunao.cn/P2303 [SDOI2012] Longge 的问题)
