ArangoDB 3.5 发布了。ArangoDB 是一个分布式原生的多模型数据库，具有灵活的文档、图形和键值数据模型。使用方便的 SQL 查询语言或 JavaScript 扩展构建高性能应用程序。

此版本亮点包括：

• 期待已久的 Streaming Transactions API，可以直接使用不同的语言驱动运行和管理 ACID 事务（已支持 Java Sync、Go、JavaScript 和 PHP）

• ArangoSearch 改进，包括可配置分析器、超快速排序索引等

• 扩展图形数据库功能，如 k-shortest 路径和新的 PRUNE 关键字

• Data Masking，可以安全地使用模糊的生产数据来实现真实的开发和测试环境

• Time-To-Live 索引、索引提示和命名索引等更新

• SmartJoins，可以针对分布式数据运行高效的共址 JOIN 操作（企业版功能）

流事务 API（Streaming Transactions API）

此版本正式引入了流事务 API（Streaming Transactions API），这是一种更简单地使用 ACID 事务的方法，不需要编写任何 JavaScript 代码。使用新的流事务 API，可以直接使用喜欢的语言对 ArangoDB 进行 BEGIN、COMMIT 与 ABORT（回滚）操作，与使用 RDBMS 类似，目前官方已经支持 Java Sync、Go、JavaScript 与 PHP。事务可以包含一系列受支持的事务操作，后跟 commit 或 abort 命令。这允许客户端以比基于 JavaScript 的事务更有效的方式构建更大的事务。

事务可以有许多配置选项，对于调用事务，可以定义以下内容：

• collections：任何写操作都需要的事务的集合

• waitForSync：一个可选的 Boolean 标志，用于强制事务在返回之前写入磁盘

• allowImplicit：允许事务从未声明的集合中读取

• lockTimeout：允许指定事务完成的最长时间（默认为 10 分钟）

• maxTransactionSize：如果使用 RocksDB 作为存储引擎（自 ArangoDB 3.4 以来的默认引擎），可以以字节为单位定义事务的最大大小

搜索引擎升级：可配置分析器和超快速排序查询

可配置分析器允许执行区分大小写的搜索、词干分析，并允许使用自己的语言特定的禁用词列表。同时还可以更好地调整 ArangoSearch 查询，包括英语、法语、德语与中文等多种语言。

新的排序索引，包括排序的查询有大幅性能提升。在为 ArangoSearch 创建视图时，现在可以指定创建此新索引并定义哪种排序顺序最适合查询要求（升序/降序）。如果查询中的排序顺序与视图中指定的排序顺序匹配，则可以直接从索引中读取结果并以超快的速度返回结果。内部基准测试表明，这些情况下性能提升高达 1500 倍。

创建排序视图可以通过`arangosh`完成：

db._createView('myView', 'arangosearch', { links : { ... }, primarySort: [ { field: 'myField', direction: 'asc' }, { field: 'anotherField', direction: 'desc' } ] })
db._query('FOR d in myView SEARCH ... SORT d.myField ASC RETURN d`); // no sorting at query time

图形数据库升级：k-shortest 路径和新的 PRUNE 关键字

新的 k-shortest 路径功能提供查询两个给定顶点之间的所有最短路径的选项，根据路径长度或路径权重返回排序结果。

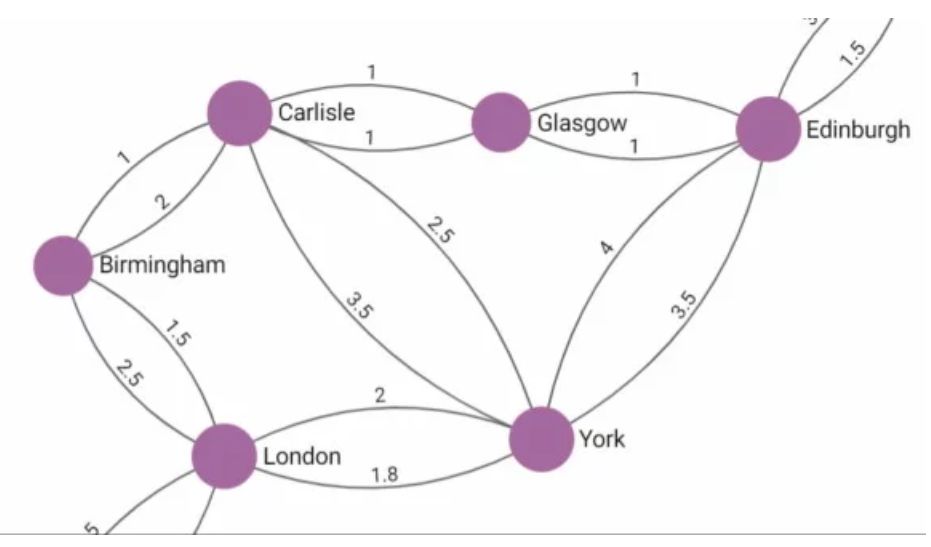
在上图的欧洲铁路的例子中，可以查询伦敦和格拉斯哥之间旅行的最短距离、最少停靠或最便宜的票价，具体取决于在边缘存储的信息。还可以想象一下将 k-shortest 路径功能运用到网络管理与威胁情报等方面。

新的 PRUNE 关键字是 AQL 图遍历查询中 FILTER 的替代方法，使用 PRUNE 允许用户减少遍历查询必须查找的文档数量。PRUNE 在图遍历中表现为停止条件，告诉遍历在满足给定条件时停止并返回完整结果路径。

数据遮掩（Data Masking）：适用于 GDPR 和 CCPA 兼容的测试和开发

在生产环境中测试新版本或新功能是很有必要的，但是，将用户名称、生日、电子邮件地址或信用卡信息等敏感数据从高度安全的生产系统导出到安全性很低的测试和开发环境，通常是不可能的，或者会导致 GDPR/CCPA（欧盟《一般数据保护条例》/《加利福尼亚州消费者隐私保护法案》）合规性问题。

ArangoDB 中新的 Data Masking 功能允许定义要进行模糊处理的敏感数据，然后生成这些集合的“掩数据”，导出以用于测试或开发目的。

此外，快速一致的集群备份功能将在下个版本 3.5.1 中出现。

更具体的更新内容查看「阅读原文」。