Title: [科普] 无刷直流电机驱动控制原理图解
文章目录
- I. 引言
- II. 直流电机的原理
- 1. 有刷直流电机和无刷直流电机的区别
- 2. 有刷直流电机的运行原理
- 3. 既是电动机又是发电机
- III. 无刷直流电机的原理
- 1. 无刷直流电机与永磁同步电机的区别
- 2. 无刷直流电机的换向控制原理
- 3. 无刷直流电机的六步换向时序
- 4. 无刷直流电机的换向检测
- III. 无刷直流电机的有感控制
- 1. 有感控制的霍尔检测
- 2. 有感控制策略
- 3. 有感控制律
- IV. 无刷直流电机的无感控制
- 1. 再谈反电动势
- 2. 无刷直流电机的无感换向时机
- 3. 无感控制的过零检测方法 —— 母线电压
- 4. 无感控制的过零检测方法 —— 虚拟中性点
- 5. 无感控制的 "三段式" 启动
- V. 无刷直流电机的调速与制动
- 1. PWM 调速与续流
- 2. 无刷直流电机的制动
- VI. 开源实例
- VII. 总结
- 附录
- A. 六步换向时序的动图
- B. 有感控制律的动图
来源说明
关于直流电机原理的介绍, 网上有海量的资料.
入行机器人好多年了, 经常为了学习或者选型要调研一下电机.
根据之前自己学习中的简单内容, 整理并分享一下.
本篇博文的定位是入门科普.
相关内容根据书本或者开源资料整理和再加工而成, 不涉专利或机密.
I. 引言
当前机器人的核心技术能力: 1.感知 (Perception)、2.决策 (Decision)、3.执行 (Execution)
未来可能还要加上认知 (Cognition), 这对当前的机器人还太奢侈.
现在市面上的机器人产品也主要围绕感知 (检测与巡检机器人) 和执行 (移动与作业机器人) 功能开展.
决策功能作为机器人的主控体现, 作为信息汇总和处理单元, 当前反倒没有感知与执行来得硬核.
机器人运动和力的输出执行依靠执行器, 执行器是动力源和机械零件的组合, 是进行机械控制的装置.
电动机 (俗称马达, Motor) 是一种最通用的执行器动力源, 无刷直流电机就是其中之一.
事实上, 电机 (Electric Machine) 是机械能与电能之间转换装置的通称, 可以分为电动机和发电机.
一般称电机时就是指电动机, 发电机会特殊说明.
作为电机的一员, 无刷直流电机 (Brushless DC Motors, BLDC) 因其在寿命和效率上的优异性能, 在机器人中应用广泛.
II. 直流电机的原理
移动机器人因为没有固定基座, 一般都以电池供电, 故所用电机主要是直流电机.
直流电机又分为有刷直流电机和无刷直流电机两种, 具有不同的原理和结构.
1. 有刷直流电机和无刷直流电机的区别
| 图示 | |
|---|---|
| 有刷直流电机 |  |
| 无刷直流电机 |  |
| 结构上的区别 | 有刷直流电机: 永磁体构成定子, 电磁线圈组成转子 无刷直流电机: 永磁体构成转子, 电子线圈组成定子 有刷直流电机的电刷和换向器转换为无刷直流电机的逆变电路 无刷直流电机的定子三相绕组采用星形 (Y形) 连接 |
| 性能上的区别 | 无刷直流电机的优势: 寿命长, 噪音低, 效率高 有刷直流电机的优势: 启动转矩大 无刷直流电机的劣势: 成本高, 控制复杂 有刷直流电机的劣势: 有火花, 寿命短 |
2. 有刷直流电机的运行原理
有刷直流电机通过电刷实现换向, 使得转子持续转动.
我们下面以转子的三个转角状态为例, 描述有刷直流电机极性循环以及运动形成.
| 状态 1 | 转子磁极 ❶ = 0 ° ❶= 0° ❶=0° |
|---|---|
| 图示 |  |
| 说明 | (1) 转子磁极 ❶ 为 S 极, ❷ 和 ❸ 为 N 极 (2) S 极处于中心, 不受力 (3) 左侧转子 N 极与定子 N 极靠近, 相互排斥 (4) 右侧转子 N 极与定子 S 极靠近, 相互吸引 (5) 转子因受到顺时针的转矩而旋转 |
| 状态 2 | 转子磁极 ❶ = 60 ° ❶= 60° ❶=60° |
|---|---|
| 图示 |  |
| 说明 | (6) 随着转子的顺时针转动, 电刷和整流子相互位置发生变化 (7) 转子 ❸ 的极性转变为 S 极, 与定子 S 极排斥, 继续顺时针旋转 (8) 转子 ❶ 此时仍为 S 极, 受到定子 N 极顺时针方向的吸引, 而继续旋转 |
| 状态3 | 转子磁极 ❶ = 120 ° ❶= 120° ❶=120° |
|---|---|
| 图示 |  |
| 说明 | (9) 此时转过120°, 电刷和整流子的位置又发生了变化 (10) 转子磁极 ❶ 由 S 极变为 N 极 此时转子的极性状态与初始位置状态相同, 转子继续顺时针旋转, 如此循环运行 |
3. 既是电动机又是发电机
反电动势 (Back Electromotive Force, Back EMF) 指有反抗电流通过趋势的电动势, 为感应电动势.
电动机转子上永磁体转动时, 改变磁场方向, 进而改变通过定子线圈中的磁通量, 定子线圈中就会产生感应电动势, 这个感应电动势即为反电动势.
反电动势总要削弱电源电动势的作用, 并阻碍磁场的改变, 即阻碍转子线圈的转动.
如果要使线圈维持原来的转动, 电源就要向电动机提供能量, 从而实现电能转化为其它形式的能。
反电动势是电机驱动控制中的最重要概念之一.
因为反电动势的存在, 使得实际直流电机运行过程中, 既呈现出电动机的行为, 又呈现发电机的行为.
即电动机不是 “纯电动机”, 而是电动机和发电机的共生.
| 直流电机的两种行为 | |
|---|---|
| 图示 |  |
| 说明 | 运行中电动机 = “纯电动机” + 发电机 启动和堵转时, 没有反电动势, 电流大, 力矩也大 高速转动, 电流被反电动势部分抵消, 力矩也小了 |
III. 无刷直流电机的原理
1. 无刷直流电机与永磁同步电机的区别
无刷直流电机和有刷直流电机区别在与是通过电刷和换向器实现换向还是通过逆变电路实现驱动换向.
另外还有一种电机和无刷直流电机 (BLDC) 很像, 就是永磁同步电机 (Permanent Magnet Synchronous Motors, PMSM).
两者的主要区别是反电动势的波形. BLDC 反电动势接近于梯形波, 而 PMSM 反电动势接近于正弦波.
BLDC 径向充磁的表贴式磁钢感应产生平顶度很宽的梯形波反电势.
但是现实世界中的波形一般都不完美, 还不足以反电动势 100% 区分两者.
但如果结合定子绕组形式 (BLDC 多集中式, PMSM 多分布式)、价格 (BLDC 相对便宜, PMSM 相对较贵)、应用场合 (移动机器人多用 BLDC, 新能源汽车多用 PMSM) 这些综合判断的话, 两者区分度还是很大的.
| BLDC 的反电动势波形 | PMSM 的反电动势波形 |
|---|---|
 |  |
2. 无刷直流电机的换向控制原理
如下图示例 (A+ C-) \text{(A+ C-)} (A+ C-) 极通电导通时, 电流由 A 极流向 C 极, 这样形成了定子合成磁场. 永磁体转子会根据定子合成磁场的方向进行旋转. 下图仅示例一极对, 多极对利用电角度概念类比实现.
| 合成磁场示意 |
|---|
 |
通过对三相交替通电 (A+ C-) \text{(A+ C-)} (A+ C-), (A+ B-) \text{(A+ B-)} (A+ B-), (C+ B-) \text{(C+ B-)} (C+ B-), (C+ A-) \text{(C+ A-)} (C+ A-), (B+ A-) \text{(B+ A-)} (B+ A-), (B+ C-) \text{(B+ C-)} (B+ C-), 完成磁场旋转. 每一步只改变其中一极的导通状态, 共六步来完成定子合成磁场旋转一周, 即每步磁场旋转 60° —— 该方法被称为 “六步换向法”. 如下图所示六步换向法的基本原理:
| 六步换向实现定子磁场的旋转 |
|---|
 |
为了实现定子磁场的旋转 (即六步换向), 需要交替有序地导通定子的三相电极. 而实现三相电极交替导通的驱动电路为三相全桥逆变电路, 控制上按照六步换向时序进行控制.
 |
|---|
 |
3. 无刷直流电机的六步换向时序
六步换向法时序, 同一时间只有两相导通 (120° 导通), 另一相不导通 (悬空).
转子每转过 60° 电角度, 定子换向一次, 定子旋转磁场在一次换向后也变化 60° 电角度, 实现同步控制.
(我们这里演示的都是一极对, 电角度和几何角度一致)
每次换向只切换一个桥臂 (只切换一相), 使得切换控制较平稳. 故换向也有人称作换相.
如下所示是转子逆时针旋转时的六步换向时序图 (顺时针旋转时, 雷同).
| 六步换向时序图 | |
|---|---|
| 第1步 | ![[六步换向时序图]_1](https://img-blog.csdnimg.cn/c0db8e41b624492c990320bc6a10c6a0.png#pic_center) |
| 第2步 | ![[六步换向时序图]_2](https://img-blog.csdnimg.cn/3b8797e682d3467daaeb8ee31bbb36f6.png#pic_center) |
| 第3步 | ![[六步换向时序图]_3](https://img-blog.csdnimg.cn/777ced2e00344e948c62423bf4e19d83.png#pic_center) |
| 第4步 | ![[六步换向时序图]_4](https://img-blog.csdnimg.cn/06ff95ff7a2f48fd98d43f52b0c16772.png#pic_center) |
| 第5步 | ![[六步换向时序图]_5](https://img-blog.csdnimg.cn/2d5f00a483d14baf92e0ce032cf2d93f.png#pic_center) |
| 第6步 | ![[六步换向时序图]_6](https://img-blog.csdnimg.cn/e1f63b3fc2a847d3ab3e3a6f01f0e1a3.png#pic_center) |
[注]: 转子逆时针旋转的六步换向时序的动画显示见附录 A.
4. 无刷直流电机的换向检测
有刷直流电机通过电刷和换向器的结构设计, 可以实现电机的同步驱动, 是机械上的实现而不需要控制律的协助.
无刷直流电机要实现六步换向时序控制, 需要通过检测 (反馈) 手段, 进行换向同步驱动控制.
根据不同的检测手段, 又将 BLDC 的驱动控制分为有感驱动和无感驱动两类.
| 特点比较 | |
|---|---|
| 有感驱动 | 霍尔传感器 (BLDC 有感控制中最常用的传感器) 采集转子位置信号, 再根据霍尔信号进行电流换相 优点: 电机启动和低速时可以做到大力矩输出; \qquad 启动时不会有抖动, 非常顺畅 缺点: 霍尔自身比较敏感脆弱易受干扰; \qquad 增加信号线 (+5根) 和安装结构; \qquad 增加体积和成本 应用场景: 车模和船模中的电调多是使用 “有感” 方式, 因为其电机需要频繁启动、停止、反转 |
| 无感驱动 | 不需要外部位置传感器, 通过检测悬空相的反电动势的过零点, 进行换向控制 优点: 成本和结构上有了大的简化; \qquad 外置驱动时电机只有三根相线 缺点: 带载、满载启动容易抖动或启动失败, 只适合固定负载启动或者空载启动的场合 \qquad 无感控制启动的时候可控性较差, 要达到一定转速后才变得可控 应用场景: 航模/无人机一般用 “无感” 方式, 因为航空发动机一旦转起来后, 在空中不需要停车 |
III. 无刷直流电机的有感控制
1. 有感控制的霍尔检测
| 霍尔传感器 120° 电角度布置时的转子角度检测 |
|---|
 |
| 一对磁极情况下, 霍尔传感器 120° 电角度布置时, 每 60° 电角度对应唯一霍尔状态, 可作为 “六步换向法” 的位置信号. |
| 霍尔传感器 60° 电角度布置时的转子角度检测 |
|---|
 |
| 一对磁极情况下, 霍尔传感器 60°电角度布置时, 每 60° 电角度对应唯一霍尔状态, 可作为 “六步换向法” 的位置信号. 注意 120° 分布和 60° 分布的霍尔信号是不同的. |
2. 有感控制策略
| BLDC 有感控制策略 |
|---|
 |
| 如左图所示, 定子电磁场旋转相位超前于转子磁场旋转相位, 产生牵引力矩 如右图所示, 定子电磁场旋转相位超前于转子磁场旋转相位 90° 时, 力矩转化率最高 (即单位电流产生的转矩最大化, 电机矢量控制 FOC 就是这个策略) [BLDC 驱动控制策略]: 在每次换相时使定子磁场领先转子磁场方向 120° 电角度, 这样在接下来转子旋转 60° 的过程中, 定子磁场与转子磁场方向的夹角从 120° 变化到 60°, 这种情况下的力矩转化率较高 |
3. 有感控制律
BLDC 有感控制就是通过位置传感器获得转子的位置 (转角), 然后通过控制定子线圈中的电流导通实现对定子磁场的调制.
使得定子磁场相位领先于转子转角相位 60°~ 120° 之间 (电角度), 这样定子磁场始终能够以较高的效率驱动转子的转动.
定子磁场就是根据转子位置数据的反馈而进行控制. 位置传感器一般选用较廉价的霍尔传感器.
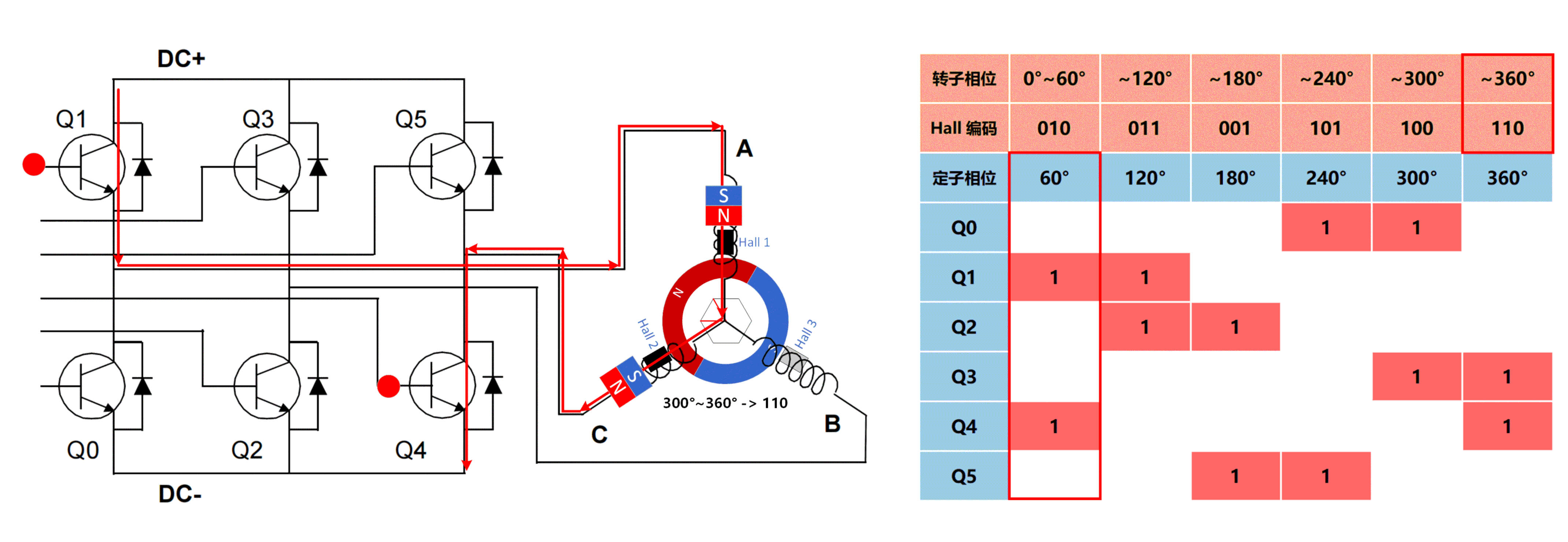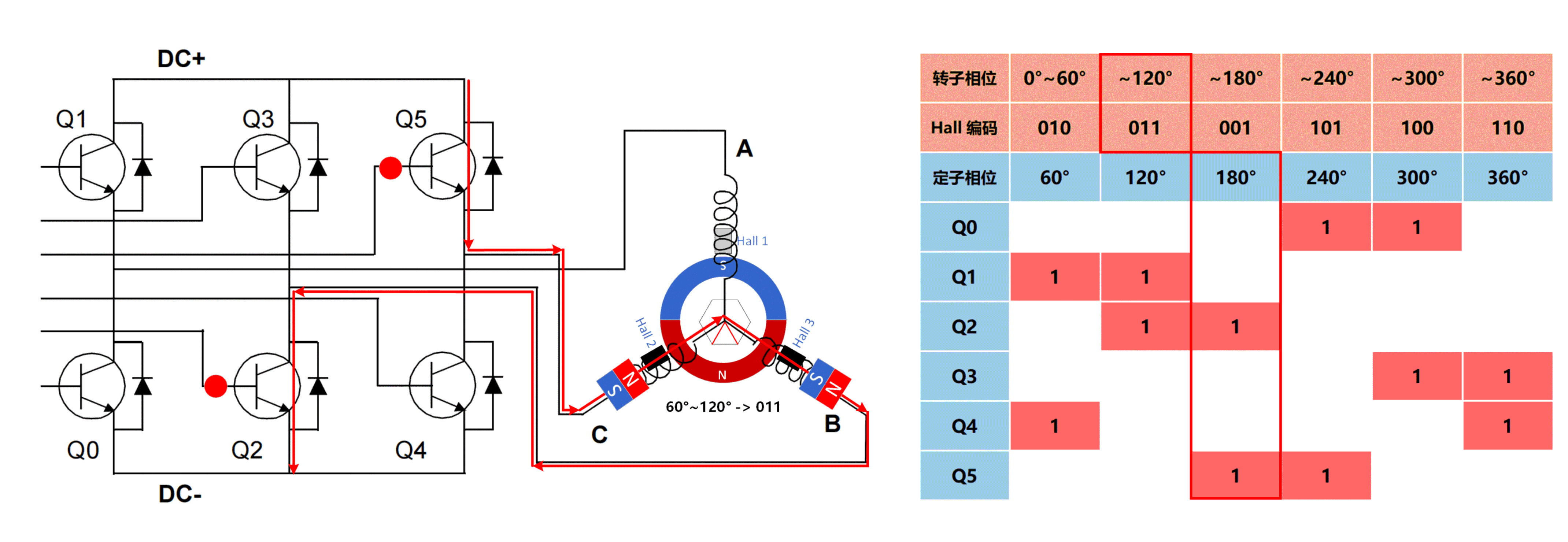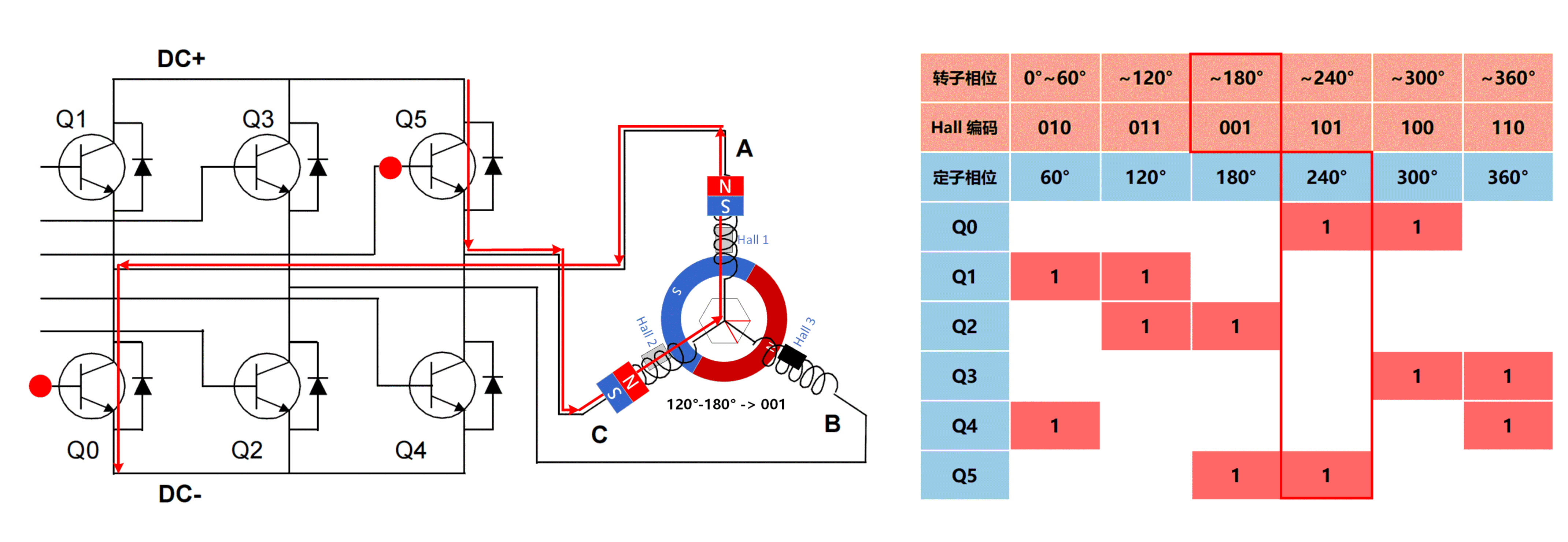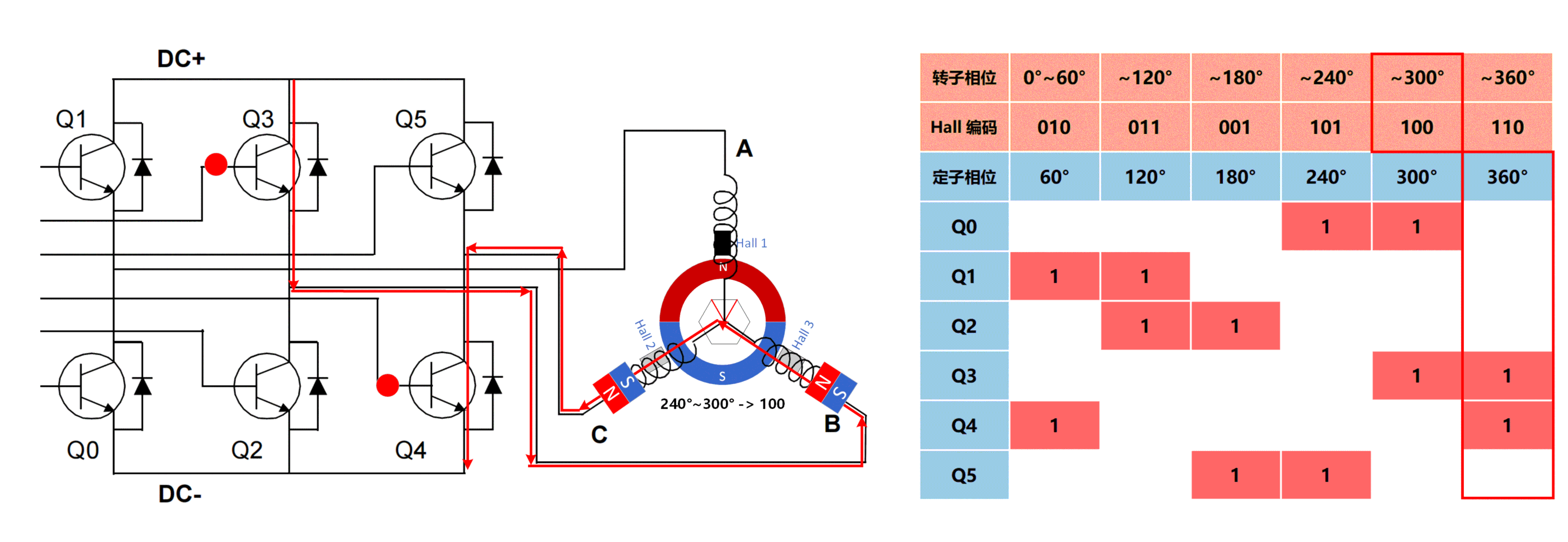
从下面各 BLDC 逆时针旋转的有感控制律图片中也可以看出:
- 转子相位进入 300° ~ 360° 区间时, 定子相位马上被控制到 60° 上;
- 转子相位达到 0° ~ 60° 区间时, 定子相位马上被控制到 120° 上;
(依此类推) … …
霍尔传感器检测作用是确定和触发 “六步换向法” 中的换向时机, 产生最优电能-机械能转换效率.
| BLDC 有感控制律 (霍尔传感器触发的六步换向法) | |
|---|---|
| 第1步 |  |
| 第2步 |  |
| 第3步 |  |
| 第4步 |  |
| 第5步 |  |
| 第6步 |  |
[注]: BLDC 逆时针旋转的有感控制律的动画显示见附录 B.
IV. 无刷直流电机的无感控制
1. 再谈反电动势
由物理知识可知感应电动势又分为: 动生电动势、感生电动势. 动生电动势是一种由于导体在磁场中运动而在导体内部产生的电动势. 感生电动势是一种由于磁场变化而在静止导体中产生的一种电动势.
BLDC 产生的感应电动势 (反电动势) 是感生电动势.
E = n Δ Φ Δ t (IV-1-1) E = n \frac{\Delta \Phi}{\Delta t} \tag{IV-1-1} E=nΔtΔΦ(IV-1-1)
其中 E E E 为反电动势, Φ \Phi Φ 为磁通量, n n n 为绕组匝数.
| 反电动势的行为 | |
|---|---|
| 靠近过程中 磁通量增加 反电动势抵抗磁通的增加 —— “你别过来” |  |
| 远离过程中 磁通量减少 反电动势抵抗磁通的减少 —— “你别走” |  |
| 磁通量没有变化时的瞬间 反电动势为 0 为反电动势过零点 —— “无所谓” |  |
2. 无刷直流电机的无感换向时机
借用有感控制控制律的图示:

转子电角度从 300° ~ 360° 之间变化时, Hall 传感器检测到的转子位置编码为 110.
当转子角度为 330° 时, B 相 (悬空相) 上的反电动势过零点, 即 B 相此刻瞬间的磁通不变.
对比有感控制的换向时机, 如需无感控制达到有感控制同样的效果, 需要在 B 相反电动势过零并延迟 30° 相位后, 执行换向 (换相) 控制.
在该换向时刻进行换向后, 定子相位为120°, 此时转子相位为 0°. 其他换向时机依次类推.
在准确检测出悬空相端电压 (反电动势) 的过零点后再延迟 30° 电角度, 即为 BLDC 无感控制的换向时机.
和有感控制一样, 在每次换相 (换向) 后的瞬时, 定子磁场 (合成磁场) 领先转子磁场方向120° 电角度. 然后在转子磁场向前转动 60° 电角度的过程中, 保持定子磁场不变, 直到下一个换向时机到来.
区别于 FOC 控制的是, FOC 控制使得定子的合成磁场始终领先转子磁场 90°, 始终保持最高效的控制. 可见在原理上 FOC 是相对六步换向法更高效和精密的控制方法, 技术难度上也更高, 本篇博文暂不展开 FOC 的内容.
我们知道了 BLDC 无感控制的换向时机取决于悬空相的反电动势过零点时刻.
那么无感控制的重点就是悬空相的过零点检测技术了.
3. 无感控制的过零检测方法 —— 母线电压
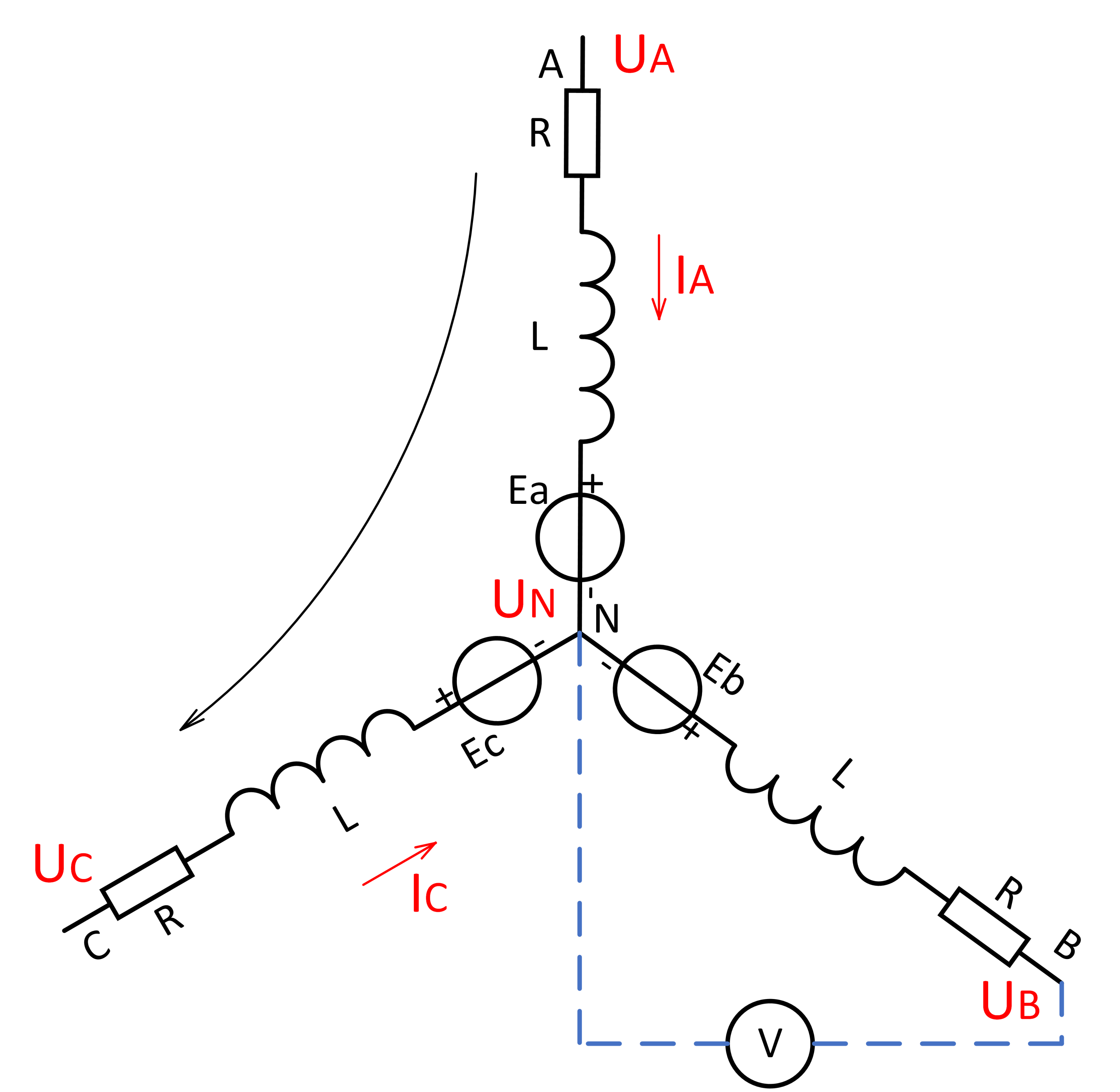
如上图所示, 是 BLDC 的定子三相绕组星形连接的等效电路图. 假设此时 B 相 (极) 为悬空相, 需要检测该相的反电动势过零点. 根据基尔霍夫电压定律 (Kirchhoff’s Voltage Law, KVL) 先建立数学模型:
U A = I A R + L d I A d t + E a + U N (IV-3-1) U_{A} = I_A R +L \frac{d I_A}{dt} + E_a +U_N \tag{IV-3-1} UA=IAR+LdtdIA+Ea+UN(IV-3-1)
U B = I B R + L d I B d t + E b + U N (IV-3-2) U_{B} = {I_B} R +L \frac{d I_B}{dt} + E_b +U_N \tag{IV-3-2} UB=IBR+LdtdIB+Eb+UN(IV-3-2)
U C = I C R + L d I C d t + E c + U N (IV-3-3) U_{C} = {I_C} R +L \frac{d I_C}{dt} + E_c +U_N \tag{IV-3-3} UC=ICR+LdtdIC+Ec+UN(IV-3-3)
其中
U A U_A UA、 U B U_B UB、 U C U_C UC 为三相绕组 A A A、 B B B、 C C C 三个极上的电势;
I A I_A IA、 I B I_B IB、 I C I_C IC 为三相绕组内的电流, 并因为 B 相悬空故有
I B = 0 (IV-3-4) I_B = 0 \tag{IV-3-4} IB=0(IV-3-4)
E a E_a Ea、 E b E_b Eb、 E c E_c Ec 为三相绕组上的反电动势;
U N U_N UN 为三相绕组的公共点 N 的电势;
L L L 为各相绕组线圈的电感.
再根据基尔霍夫电流定律 (Kirchhoff’s Current Law, KCL) 建立方程
I A + I C = 0 (IV-3-5) I_A +I_C =0 \tag{IV-3-5} IA+IC=0(IV-3-5)
由式 (IV-3-1) 和式 (IV-3-3), 并结合式 (IV-3-5) 可知
U A + U C = E a + E c + 2 U N (IV-3-6) U_A + U_C = E_a +E_c + 2 U_N \tag{IV-3-6} UA+UC=Ea+Ec+2UN(IV-3-6)
由式 (IV-3-2) 结合式 (IV-3-4) 可知
E b = U B − U N (IV-3-7) E_b = U_{B} - U_N \tag{IV-3-7} Eb=UB−UN(IV-3-7)
也就是说, 悬空相上的反电动势就是悬空相对应极 (端) 的电势减去中性点的电势.
现在的问题是: BLDC 三相线圈的公共点 (中性点) N 在电机内部, 并没有引出, 不能直接测量得到中性点的电势 U N U_N UN.
在 B 相的反电动势过零点时刻, 因为 A 相和 C 相在几何上相对于 B 相呈对称布局, 故A 相和 C 相的磁通量变化率绝对值相同但符号相反, 即
Δ Φ A + Δ Φ C = 0 (IV-3-8) \Delta \Phi_A + \Delta \Phi_C = 0 \tag{IV-3-8} ΔΦA+ΔΦC=0(IV-3-8)
由反电动势的计算公式 (IV-1-1) 可知
E a + E c = 0 (IV-3-9) E_a +E_c = 0 \tag{IV-3-9} Ea+Ec=0(IV-3-9)
那么在 B 相的反电动势过零点时刻, 式 (IV-3-6) 和式 (IV-3-7) 可以简化为
{ U A + U C = 2 U N E b = U B − U N ⇒ E b = U B − U A + U C 2 (IV-3-10) \left\{ {\begin{aligned} &U_A + U_C = 2 U_N \\ &E_b = U_{B} - U_N \end{aligned}} \right. \quad \Rightarrow\quad E_b = U_{B} - \frac{U_A + U_C}{2} \tag{IV-3-10} {UA+UC=2UNEb=UB−UN⇒Eb=UB−2UA+UC(IV-3-10)
反电动势过零点时刻 E b = 0 E_b =0 Eb=0, 只需要检测并验证下式是否成立
U B − U A + U C 2 = ? 0 (IV-3-11) U_{B} - \frac{U_A + U_C}{2} \,\,{\color{red}{\overset{?}{=}}}\,\, 0 \tag{IV-3-11} UB−2UA+UC=?0(IV-3-11)
数学上的推导是比较简明的, 实际应用如何处理呢?
上式中 U B U_B UB 对应悬空相的端电压. 因为存在一相悬空故电机驱动的输入的母线电压全部加载于未悬空的 A 相和 C 相, 即 U A + U C U_A +U_C UA+UC 是母线电压.
也就是说, 通过测量悬空相的端电压, 并将其与母线电压的一半进行对比, 即可确定悬空相反电动势过零点的时刻.
进一步, 采用分压电阻对端电压和直流母线电压进行分压, 使分压后的被测信号在采样单元允许的输入范围内.
电路实现如下图所示.
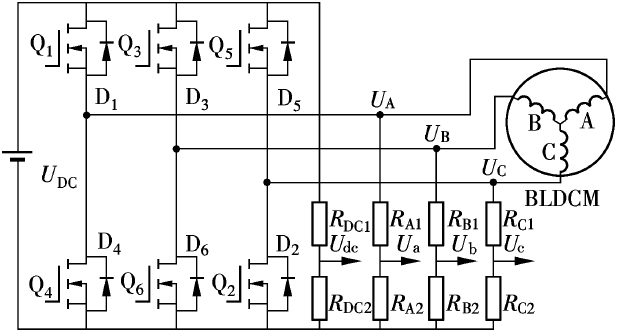
4. 无感控制的过零检测方法 —— 虚拟中性点
因为 “BLDC 三相线圈的公共点 (中性点) N 在电机内部, 并没有引出, 不能直接测量得到中性点的电势 U N U_N UN”, 但是也可以构造虚拟中性点来模拟真实中性点的电势.
下图所示是虚拟中性点的原理图:
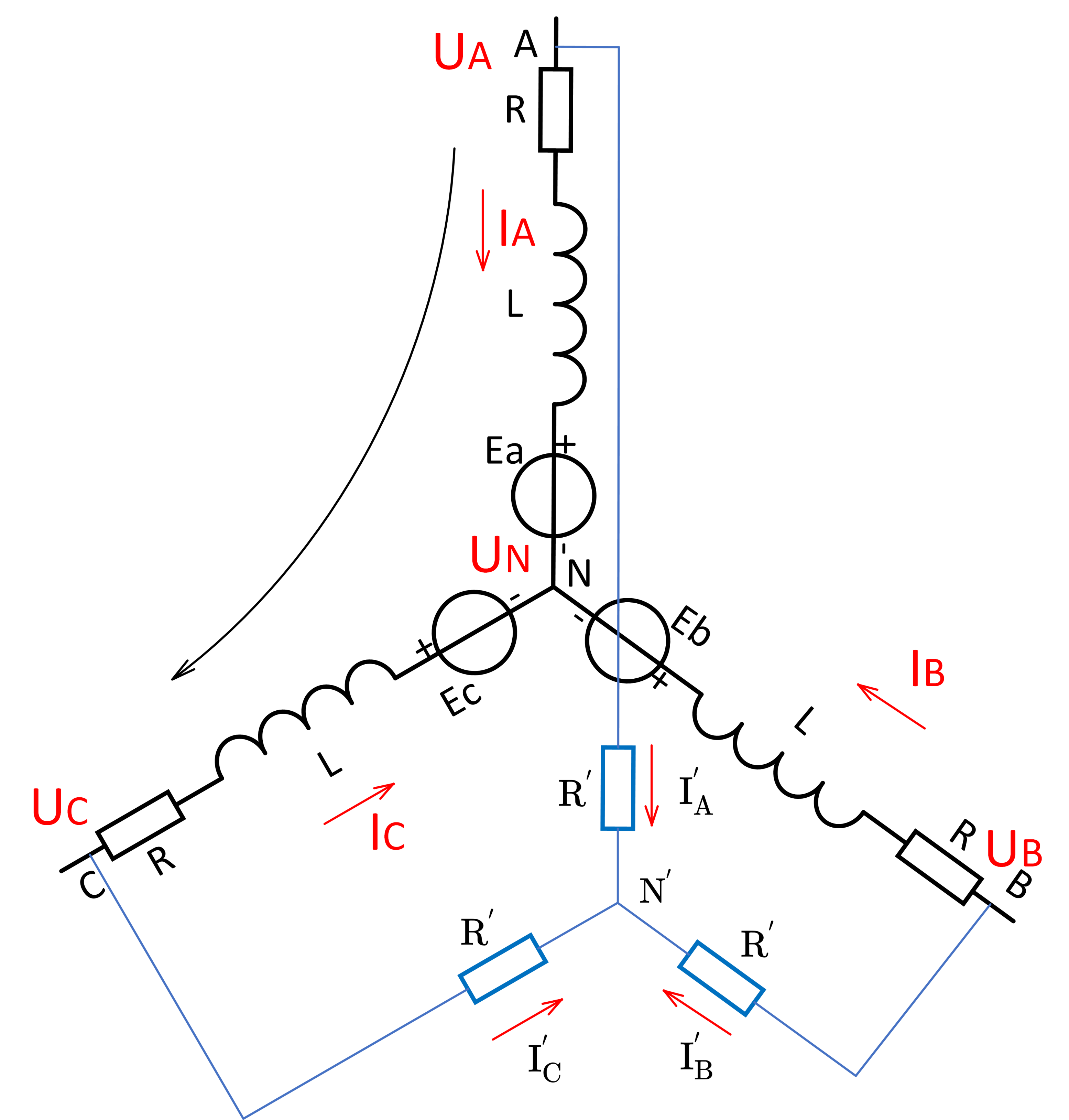
先针对 BLDC 三相绕组建立数学公式
{ U A = I A R + L d I A d t + E a + U N U B = I B R + L d I B d t + E b + U N U C = I C R + L d I C d t + E c + U N I A + I B + I C = 0 E a + E b + E c = 0 (IV-4-1) \left\{{ \begin{aligned} &U_{A} = I_A R +L \frac{d I_A}{dt} + E_a +U_N \\ &U_{B} = {I_B} R +L \frac{d I_B}{dt} + E_b +U_N \\ &U_{C} = {I_C} R +L \frac{d I_C}{dt} + E_c +U_N \\ &I_A + I_B + I_C = 0\\ &E_a + E_b + E_c =0 \end{aligned} }\right.\tag{IV-4-1} ⎩ ⎨ ⎧UA=IAR+LdtdIA+Ea+UNUB=IBR+LdtdIB+Eb+UNUC=ICR+LdtdIC+Ec+UNIA+IB+IC=0Ea+Eb+Ec=0(IV-4-1)
上式中第 5 个式子, 在悬空相反电动势过零时刻成立, 即此时反电动势之和为零 (参考式 (IV-3-9)). 将式 (IV-4-1) 中前三行式子两侧各自相加, 并考虑后两个式子, 得到悬空相反电动势过零时刻实际三相绕组中性点 N 的电势为
U A + U B + U C = 3 U N (IV-4-2) U_A +U_B + U_C = 3 U_N \tag{IV-4-2} UA+UB+UC=3UN(IV-4-2)
再针对虚拟中性点建立数学公式
{ U A = I A ′ R ′ + U N ′ U B = I B ′ R ′ + U N ′ U C = I C ′ R ′ + U N ′ I A ′ + I B ′ + I C ′ = 0 (IV-4-3) \left\{ {\begin{aligned} U_A = I_A^{'} R^{'} + U_{N^{'}}\\ U_B = I_B^{'} R^{'} + U_{N^{'}}\\ U_C = I_C^{'} R^{'} + U_{N^{'}}\\ I_A^{'} + I_B^{'} + I_C^{'} = 0 \end{aligned}} \right. \tag{IV-4-3} ⎩ ⎨ ⎧UA=IA′R′+UN′UB=IB′R′+UN′UC=IC′R′+UN′IA′+IB′+IC′=0(IV-4-3)
对式 (IV-4-3) 中前三式两侧相加, 得到虚拟中性点 N ′ \rm N^{'} N′ 的电势
U A + U B + U C = 3 U N ′ (IV-4-4) U_A +U_B + U_C = 3 U_{N^{'}} \tag{IV-4-4} UA+UB+UC=3UN′(IV-4-4)
结合式 (IV-4-2) 和式 (IV-4-4) 得到
U N = U N ′ (IV-4-5) U_N = U_{N^{'}} \tag{IV-4-5} UN=UN′(IV-4-5)
即反电动势过零点时, 虚拟中性点与三相绕组中性点电压一致.
结合式 (IV-3-7) 和式 (IV-4-5),
E b = U B − U N ′ (IV-4-6) E_b = U_{B} - U_{N^{'}} \tag{IV-4-6} Eb=UB−UN′(IV-4-6)
反电动势过零点时刻 E b = 0 E_b =0 Eb=0, 只需要检测并验证下式是否成立
U B = ? U N ′ (IV-4-7) U_{B} \,\, {\color{red}{\overset{?}{=}}} \,\, U_{N^{'}} \tag{IV-4-7} UB=?UN′(IV-4-7)
同样地, 数学上的推导是比较简明的, 实际应用如何处理呢?
虚拟中性点的检测电路如下:

电路中, 分压 (divider) 以获得合适检测范围, 滤波 (filter) 滤除尖峰、高次谐波.
让悬空相端电压与虚拟中性点电压进行比较, 以此检测反电动势是否过零点.
比如后面所列的开源方案 “MikroKopter 电调” 就是采用虚拟中性点进行过零点检测.
5. 无感控制的 “三段式” 启动
如下两个原因使得 BLDC 无感控制的平稳启动成为难题,
(1) 没有位置传感器反馈转子的位置以掌握控制换向的时机而让电机逐渐平稳运转起来
(2) 初始时刻转速较慢且不平稳, 故反电动势还微弱且紊乱, 无法利用反电动势过零点检测来确定转子位置与换向控制的时机
为了解决这个启动难题, 一般使用如下表描述的 “三段式” 启动法来启动无感的 BLDC:
| 启动阶段 | 控制方法 |
|---|---|
| 转子预定位 | 给任意两相通电, 通电一段时间后, 转子会转到与该通电状态对应的预知位置, 完成转子的预定位 (需电流控制器保证电流不超过最大值) |
| 外同步加速 | 根据预先设计好的优化加速曲线, 不断提升换相信号的频率及增大端电压, 实现电机的外同步加速(开始获得有效转子位置信号, 即过零点检测信号, 电机处于他控式同步电机状态) |
| 运行状态切换 | 当电机加速到一定转速后, 就可以准确地检测到反电动势的过零点信号了. 此时可用该过零信号代替外同步信号, 实现外同步运转到自同步运转的切换(转子磁势通常平均滞后定子磁势 90° 电角度 —— 60° ~ 120° 之间变化, 使得单位电流产生的转矩最大化) |
无刷直流电机的无感启动尚且这么复杂, 要想频繁地正反转切换控制就更麻烦了. 实际使用中只能避开这种应用需求, 转而采用有感控制.
V. 无刷直流电机的调速与制动
1. PWM 调速与续流
无刷直流电机也采用脉宽调制技术 (Pulse Width Modulation, PWM) 进行调速. PWM 是最常用的电机调速方式, 实现宽转速、灵活调速, 频率在几百 Hz 到几十 KHz 之间. 通过 PWM 波对桥式逆变功率管的开关状态进行调制, 达到对相电流的控制和调节, 从而控制电机转速.
根据无刷直流电机在每个开关管导通的 120° 电角度的时间内, 不同的斩波方法, 可以将 PWM 调制分为五种模式:
- H_PWM-L_PWM 模式
- ON_PWM 模式
- PWM_ON 模式
- H_PWM-L_ON 模式
- H_ON-L_PWM 模式
如 PWM-ON 模式, 在 120° 导通区间, 对应的两个开关管前 60° 采用 PWM 调制, 后 60° 则恒通.
又如 H_PWM-L_ON 模式, 上桥斩波而下桥恒通. 在每个通电状态中, 只对上桥臂进行 PWM 调制, 而下桥臂保持恒通. 该模式能有效的降低电机的转矩脉动, 特别是在高速情况下.
H_PWM-L_ON 模式中, 高电压端 PWM 驱动上桥, 低电压端可由普通 IO 驱动下桥, 如图 “驱动形式” 所示.
PWM 调速中, 需要考虑 PWM 波快速跳转与通断时, 元器件击穿问题或者电流续流问题. 这是就需要逆变电路中的续流二极管发挥作用了.
如图 “续流回路” 所示, 当 PWM 由高电平进入低电平, Q1 由导通变为关断, 原回路消失. 需利用仍然导通的 Q4 与一直关断的 Q0 的续流二极管构成回路, 进行续流.
续流二极管起到了平缓电流的作用, 不致电感感应电压太高而击穿元器件, 同时能够平滑电机输出力矩. 有了续流回路, PWM 调速才得以可行.
| H_PWM-L_ON 模式 | |
|---|---|
| 驱动形式 |  |
| 续流回路 |  |
2. 无刷直流电机的制动
| 制动分类 | 制动方法 | 制动控制描述 |
|---|---|---|
| 机械制动 | 抱闸方法 | 如电磁抱闸 |
| 电气制动 | 短接制动 | 将系统动能转换成电能消耗在定子绕组上 让电机的驱动MOS管上桥臂 (或者下桥臂) 全部导通而下桥臂 (或者上桥臂) 截止状态, 电机的三相定子绕组全部被短接 绕组的电阻比较小, 能产生很大的短路电流, 使电机瞬时产生极大的制动力矩, 能够达到快速刹车的效果 |
| ~ | 能耗制动 | 将系统动能转换成电能消耗在制动电阻上 |
| ~ | 反接制动 | 反接制动是将电机绕组接向电源的极性对调, 使得驱动电源极性与反电动势电源极性一致 两者叠加产生很大的制动电流, 制动效果明显但产生热量大 |
| ~ | 回馈制动 | 将机械能转换为电能, 反馈到储能装置 (无法用于故障、急停、断电) |
VI. 开源实例
无刷直流电机的六步换向驱动控制, 已经比较成熟了, 能够找到不少开源方案. 另外, 市面上也有较多封装好的芯片可选用.
| 序号 | 开源项目 | 网址 |
|---|---|---|
| 1 | MikroKopter 电调 | https://wiki.mikrokopter.de/en/BL-Ctrl_V1x-INFO |
| 2 | Odrive | https://odriverobotics.com/ |
| 3 | VESC 本杰明电调 | http://vedder.se/2015/01/vesc-open-source-esc/ |
| 4 | simpleFOC (Arduino library) | https://simplefoc.com/ |
| 5 | MIT开源 (四足机器人的电机) | https://github.com/bgkatz/3phase_integrated https://build-its.blogspot.com/ |
| 6 | STM32 Motor Control Software Development Kit (MCSDK) FULL source code | https://www.st.com/en/embedded-software/x-cube-mcsdk-ful.html |
VII. 总结
本博客文章主要涉及无刷直流电机的电调相关的基本概念:
- 直流电机的基本概念和原理
- 无刷直流电机的 “六步换向法”
- 无刷直流电机的有感控制
- 无刷直流电机的无感控制
- 无刷直流电机的调速与制动
最后列举了开源方案供参考和研究.
(如有问题, 请指出, 谢谢!)
附录
A. 六步换向时序的动图
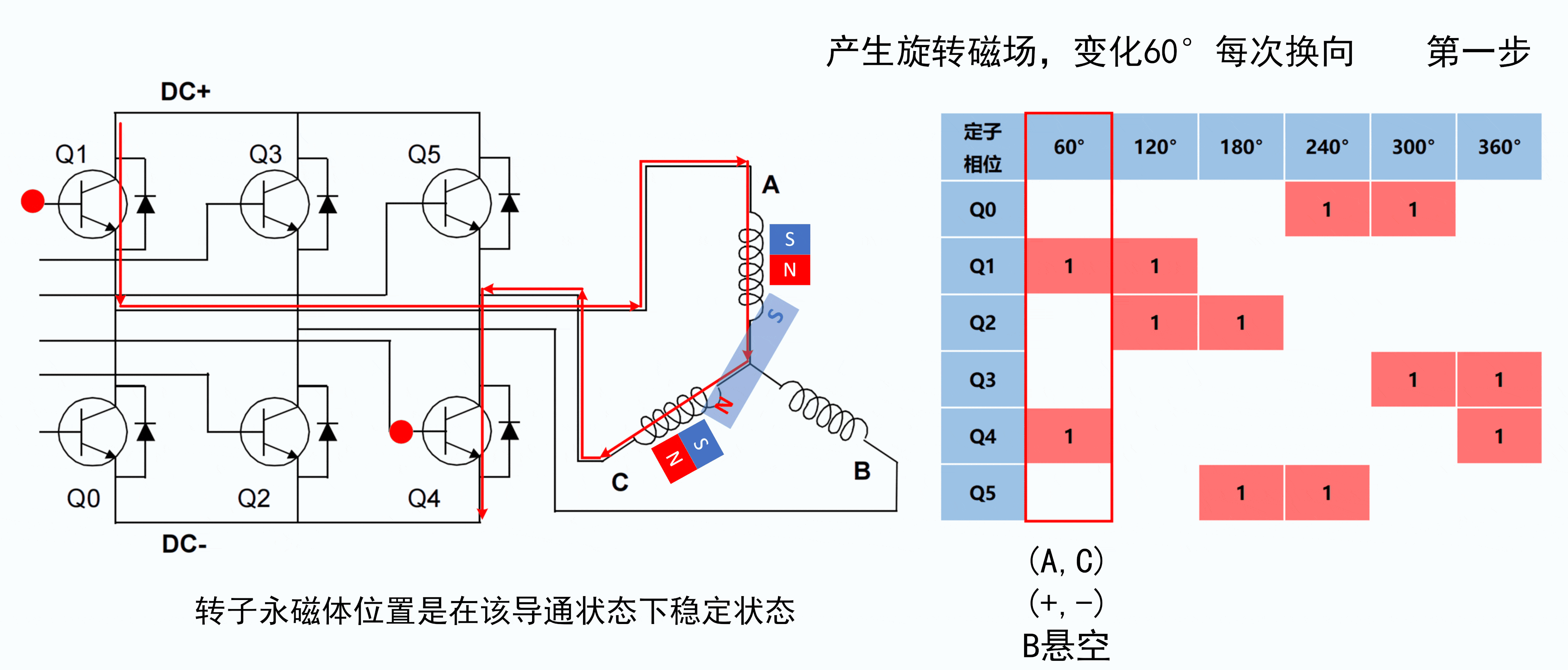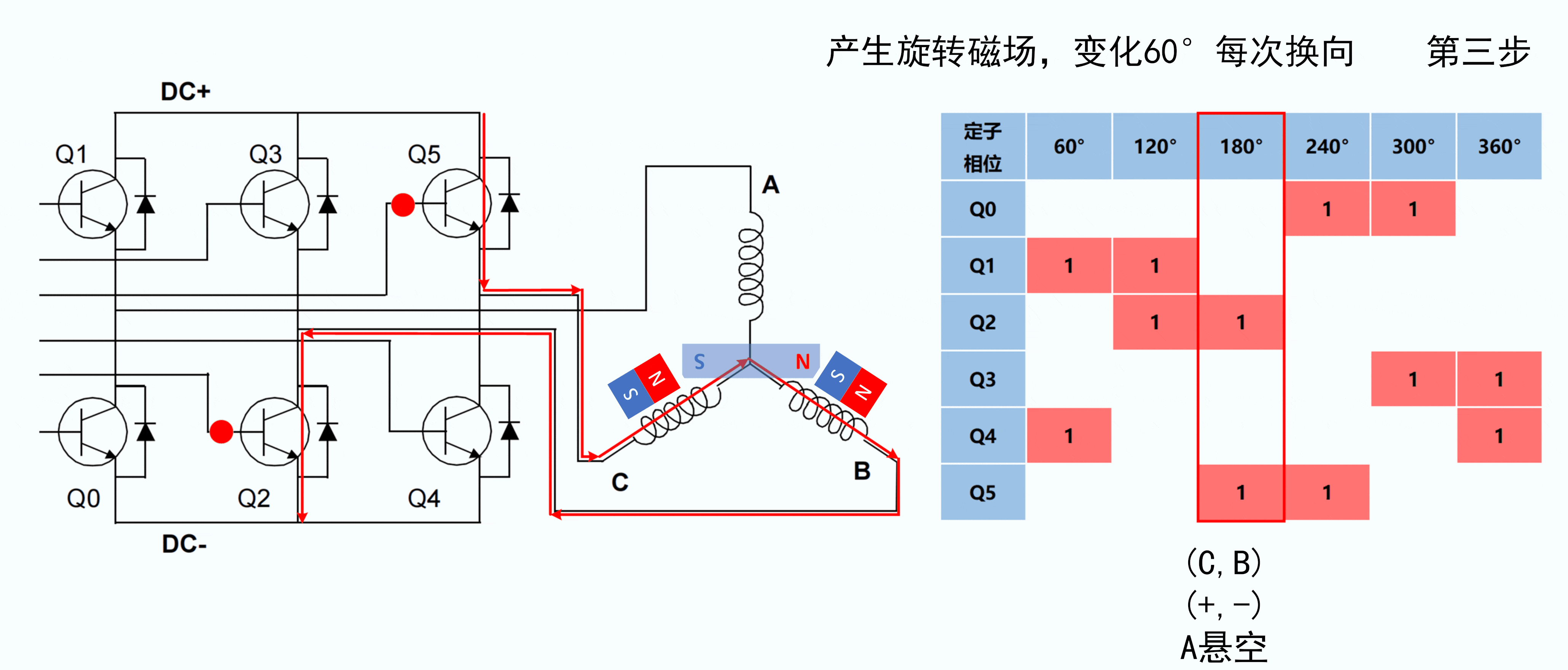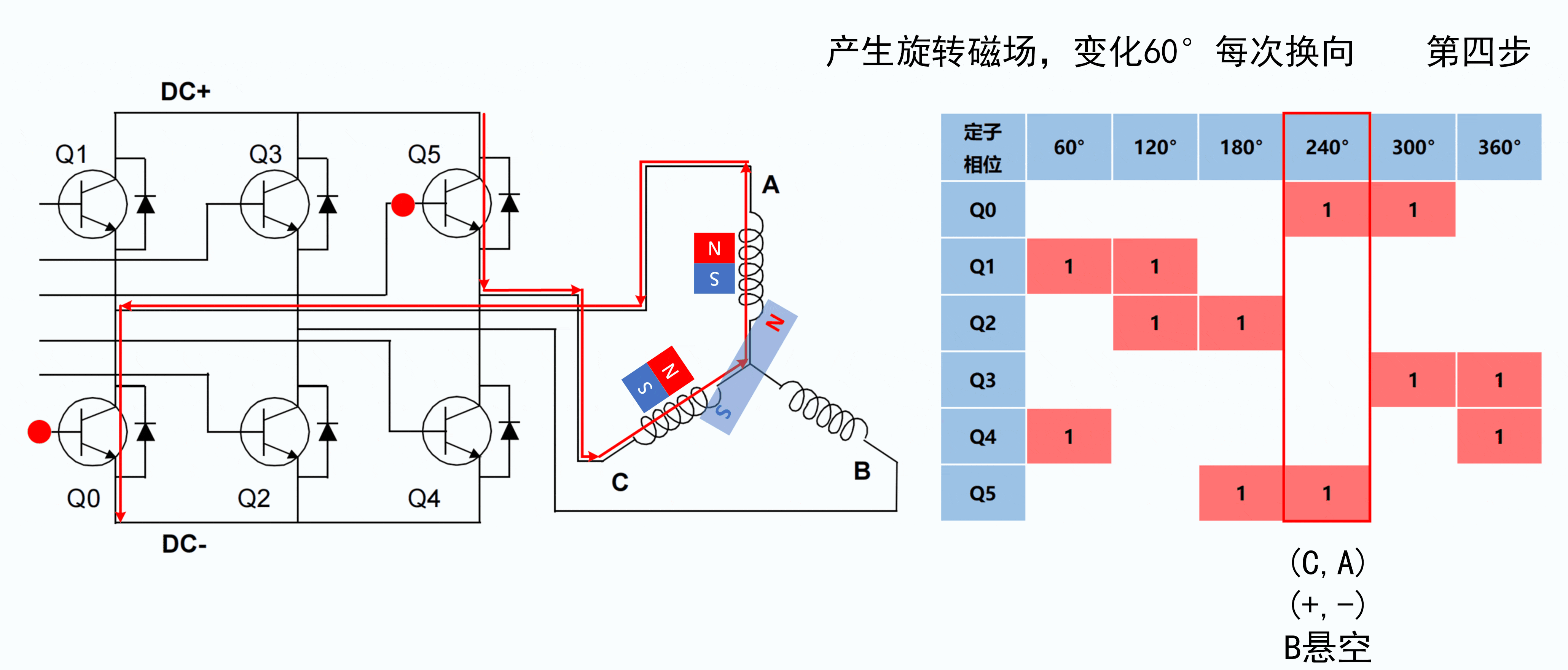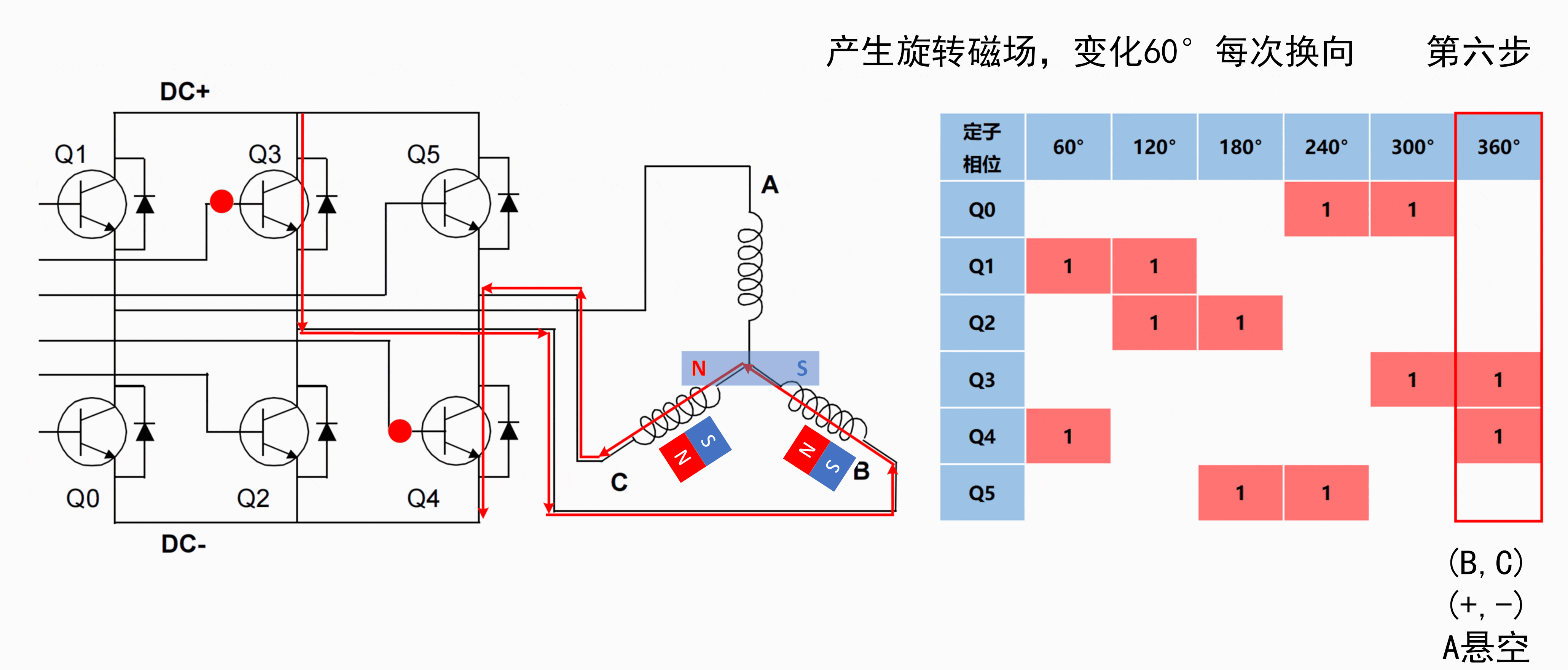
B. 有感控制律的动图