目录

1.位图

位图的实现

题目变形一

题目变形二

题目变形三

总结：

2.布隆过滤器

概念

布隆过滤器的实现

3.哈希切割的思想

1.位图

     哈希表和位图是数据结构中常用的两种技术。哈希表是一种数据结构，通过哈希函数把数据和位置进行映射，来实现快速的寻找、插入和删除操作。哈希表适用于海量数据处理，索引，数据压缩等方面有广泛应用123. 位图主要用于海量数据处理，索引，数据压缩等方面有广泛应用。位图的应用场景包括：

1. 给定100亿个整数，设计算法找到只出现一次的整数；

2. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

3. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数。

如下题目：

位图的实现

0.5G我们开不出bit类型的，我们只能开出整形或字符类型的。因此这里直接用vector来映射，因此我们需要计算出映射的位置。

如判断x是否存在,则我们需要计算x在第几个整形的第几个bit位上。

template<size_t N>class bitset
{
public:bitset(){_bit.resize(N/32);}void set(size_t x){size_t i = x / 32;//第几个整形size_t j = x % 32;//第几个位//找到该位置并置1 ，利用位运算计算//注意左移是向高位移，右移是向低位移_bit[i] |= (1 << j);//这里1左移再或上原数据，重新赋值后，该比特位就修改成1}void reset(size_t x){//与set相反，这里是将原来的x有存在变为不存在，不存在变为存在size_t i = x / 32;//第几个整形size_t j = x % 32;//第几个位//找到该位置//1变0   0变1_bit[i] &= ~(1 << j);}//检测是否中存在，即该位置是1还是0bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _bit[i] & (1 << j);}
private://数据个数足够大，用16进制表示std::vector<int> _bit;size_t size;
};

/用两个数组表示两个bit位   
//用两位bit位映射一个数三种状态，存在，不存在，个数
//00 不存在  01存在   10两个以上的个数
template<size_t N>class twobitset
{
public:void set(const size_t x){if (bit1.test(x) == false && bit2.test(x) == false)//0 0 -> 0 1{bit2.set(x);}else if (bit1.test(x) == false && bit2.test(x) == true) //0 1 -> 1 0 {bit1.set(x);bit2.reset(x);}}
private:bitset<N> bit1;bitset<N> bit2;
};

题目变形三

template<size_t N>class twobitset
{
public:void set(const size_t x){if (bit1.test(x) == false && bit2.test(x) == false)//0 0 -> 0 1{bit2.set(x);}else if (bit1.test(x) == false && bit2.test(x) == true) //0 1 -> 1 0 {bit1.set(x);bit2.reset(x);}else if (bit1.test(x) == true && bit2.test(x) == false;)// 10 ->11{bit1.set(x);bit2.set(x);}}
private:bitset<N> bit1;bitset<N> bit2;
};

2.布隆过滤器

概念

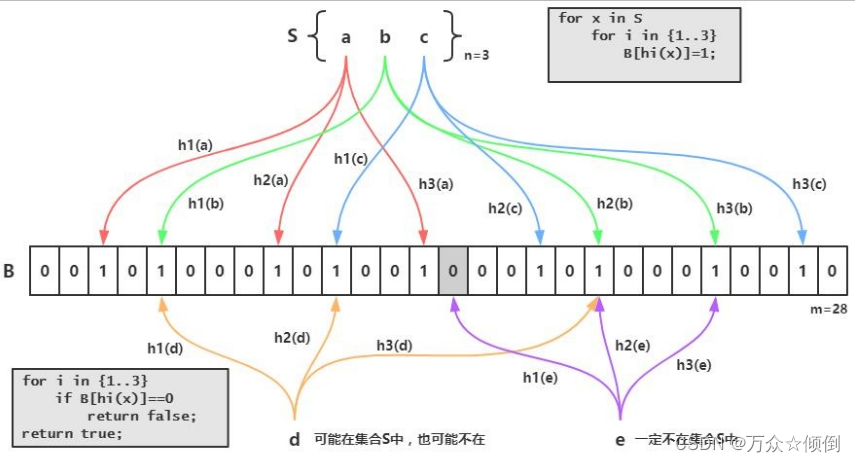
布隆过滤器是一种概率型数据结构，用于判断一个元素是否在一个集合中。它可以节省空间和时间，但有一定的误判率：

1. 布隆过滤器的核心是一个位数组，即一个只包含0和1的数组，以及一组哈希函数，即一组可以将任意元素映射到位数组的索引的函数。

2. 当要添加一个元素时，先用哈希函数计算出它在位数组中的多个索引，然后将这些索引对应的值都设为1. 当要检查一个元素是否存在时，也先用哈希函数计算出它在位数组中的多个索引，然后检查这些索引对应的值是否都为1. 如果都为1，说明元素可能存在，如果有一个为0，说明元素一定不存在。

上述说了位图，我们知道位图可以来查找大量整形数据，但是对于其他类型，如字符型，就无法去查找，此时我们就需要有一种方法将他搞成整形。

直接用ascll码肯定不行，再通过哈希字符串算法转化一下，但是仍会有较大的冲突，还是有大概率的值是一样的，为了减少这些冲突，我们让一个字符串对应三个或者更多的哈希字符串算法转化后的整形，只有当这些整型值都存在的时候才存在，大大减少了重复带来的问题。各种字符串Hash函数 - clq - 博客园 (cnblogs.com)

但是还是存在问题：即使我们让一个字符串对应了三个转化后的数，但还是存在别的字符串也会对应这三个转化后的数（将不存在的判断为存在的），我们只能尽可能的减少这种情况，因此是否存在我们还是有不确定因素，但不存在我们一定能够能确定。

一个字符串对应的三个整数的对应比特位设置为1.

总的来说，存在误判率，但概率已经不是很大了。

那么如何选择n（插入元素个数）和k（映射的个数）的值呢？

有人给出了公式计算这里的m是布隆过滤器的长度。我们先以k=3先来实现。

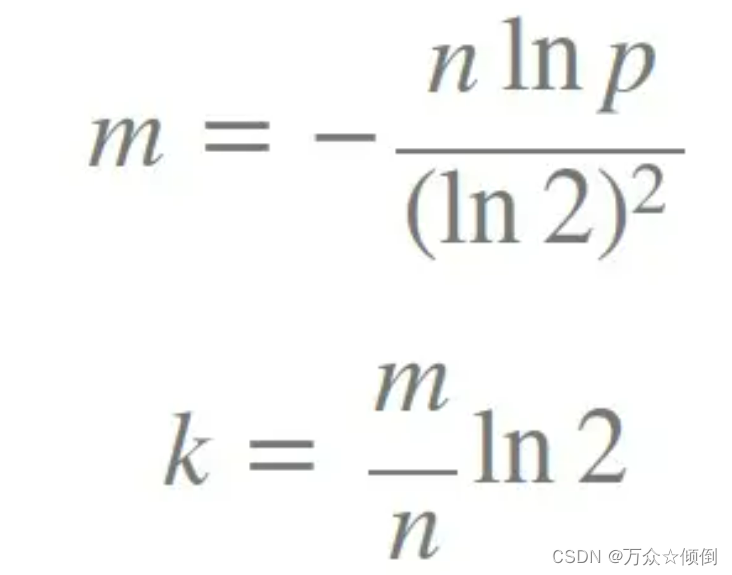
布隆过滤器的实现

#pragma once
#include"bitset.h"
//这里我们就选用3个映射值来对应一个字符串，每一个映射值我们选取一种hash字符串算法
#include<string.h>
struct BKDR
{size_t operator()(const std::string& key){// BKDRsize_t hash = 0;for (auto e : key){hash *= 31;hash += e;}return hash;}
};
struct AP
{size_t operator()(const std::string& str){size_t hash = 0;int i = 0;char ch = str[i];for (auto ch: str){if ((i & 1) == 0){hash ^= ((hash << 7) ^ ch ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));}i++;}return hash;}
};
struct SDB
{size_t operator()(const std::string& str){size_t hash = 0;for(auto ch:str){hash = 65599 * hash + ch;}return hash;}
};
template<size_t N,class K=std::string,class HashFunc1= BKDR,class HashFunc2 = AP,class HashFunc3 = SDB>
class BloomFilter
{
public://这里的类型就用泛型了void set(const K& key){//三个值来映射size_t hash1 = HashFunc1()(key) % N;size_t hash2 = HashFunc2()(key) % N;size_t hash3 = HashFunc3()(key) % N;_bit.set(hash1);_bit.set(hash2);_bit.set(hash3);}bool test(const K& key){size_t hash1 = HashFunc1()(key) % N;size_t hash2 = HashFunc2()(key) % N;size_t hash3 = HashFunc3()(key) % N;//只有当三个映射值都存在是才能表示存在if (_bit.test(hash1) == true&& _bit.test(hash2) == true&& _bit.test(hash3) == true){return true;//存在误判}return false;}/*double wrongrate(){return  }*/private://用位图封装bitset<N> _bit;
};

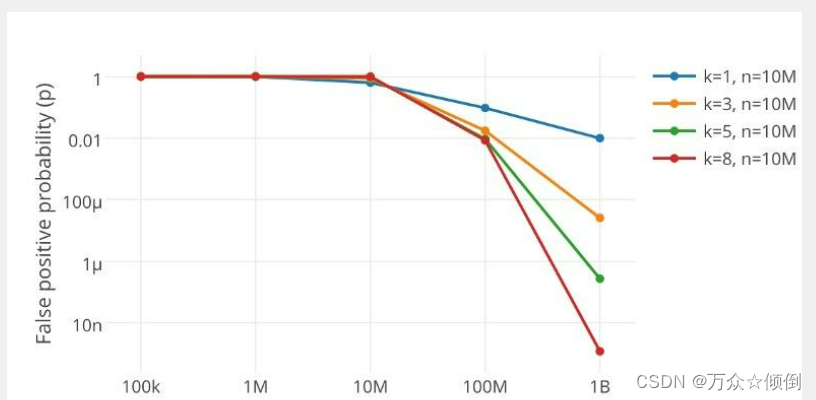
 事实上，空间开得越多，选用的映射值越多，都会之误判律极大地降低。

   对于布隆过滤器，一般是不支持删除的，我们在删除一个值这会影响以他的字符串成员存在变成不存在，如若像删除，就必须要引用计数，增加计数位（多个比特位），即对应的哈希值在每一次被set之后，对应的计数位++，判断是否存在时，同时添加计数位是否为零，其次删除后，就减减计数位的值，不过还是消耗了空间。

3.哈希切割的思想

​​​​​​​     哈希切割是一种将大文件分割成若干个小文件的方法，以便于处理海量数据。该方法使用哈希函数将相同的数据分配到同一个文件中。这种方法可以用于处理日志文件等大小超过100GB的文件

例题：