主要讲解 component 的创建
以及vue插件的安装
Vue.js Devtools
为谷歌浏览器的Vue插件,可以在调试工具内查看组件的数据等
下载
有两种下载方式
1. 谷歌应用商店
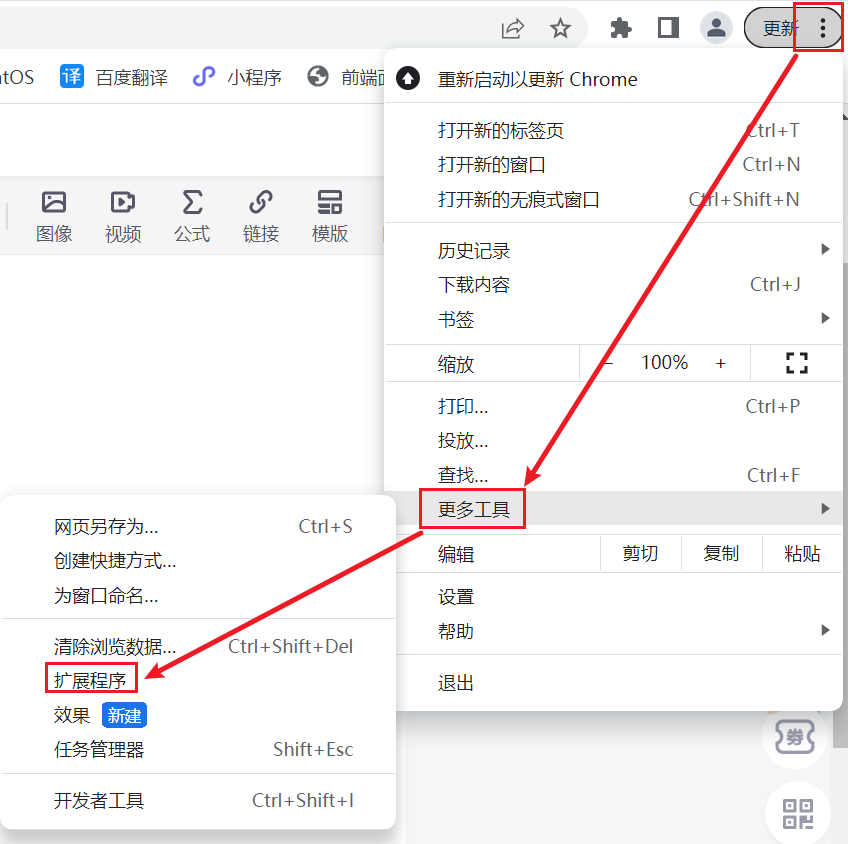

打开Chrome应用商店去下载,这个方法需要魔法
2. 极简插件
极简插件官网_Chrome插件下载_Chrome浏览器应用商店
搜索 Vue

这个就为我们需要的插件

推荐下载,下载后解压

把后缀为 crx 的文件拖动到扩展应用内

添加扩展应用,就可以使用该插件了
components 文件
components文件为放置需要复用的组件的文件
新建组件
在src内创建 components 文件夹
在文件夹内新创建 abc.vue 文件
在 abc 文件内写入需要复用的内容
使用组件
在要使用的页面内先引用
import person from './components/person.vue'在 components 内注册
export default {name:'App', // 组件名components: {person} // 注册组件
}在结构上使用该组件
<template><div class="app"><h1>hello,world!</h1><person></person></div>
</template>![[C++][算法基础]n-皇后问题(DFS)](http://pic.xiahunao.cn/[C++][算法基础]n-皇后问题(DFS))



常用操作)
删除有序数组中的重复项(79)排序矩阵查找)

)

】)
)





)
 - 17 管理科学-运筹学基础 (1)》)

