一、最小路径和
1、题目解析
就是一个人从左上往做下走，每次只能往右或者往下，求他到终点时，路径上数字和最小，返回最小值
2、算法原理
a状态表示方程
小技巧：经验+题目要求
用一个二维数组表示，创建一个二维数组
dp[i][j] 表示当前从起点到当前节点的最小值
b状态转移方程
一个小技巧：找到最近的一步，划分问题
能到达dp[i][j]的只有一条路径，上或者左边，选择一个两者较小的值。因为dp[i-1][j]或者dp[i][j-1]也是表示他那个节点对路径最小值——问题进入闭环
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]
c初始化
以下面这张图为例，为了避免越界访问我们本来应该在1,1的位置开始遍历的。给第一行和第一列进行初始化。
为了简化这个过程，我们给它多创建一行多创建一列，再给里面赋上合适的值这样避免了越界访问，也避免了初始化繁琐的操作，我们可以直接进行填表。
既然要选取较小值，那我们就直接弄上最大值INT_MAX，然后在0,1和1,0的位置附上0就行了，这样dp[1][1]就能保证刚好就是grid[0][0]，这样从1开始的每一列都是获取上面的路径和，每一行都是获取左边的路径和，这样就是合理的赋值。
这其实就是运用了虚拟节点来进行初始化，简化初始化的行为。
这种方法需要注意两点：
- 进行合理赋值，保证后面填表的值是正确的
- 注意取值的下标映射
因为我们的dp表是多了一行多了一列，我们需要i-1,j-1才能取到正确的值
d填表顺序
从左到右，从上到下
e返回值
dp[m][n]
3、代码
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {//建dp表//初始化//填表//返回值int m=grid.size();int n=grid[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));dp[0][1]=0;dp[1][0]=0;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];}}return dp[m][n];}
};二、地下城游戏
1、题目解析
这道题相较于第一题多了负数，但是还是有可以一样的处理——进行相加，并且还多了一个限制条件，骑士的值不能为零。也是只能向下和向右走。不过这道题需要返回骑士需要救到公主所需最低的健康值。
2、算法原理
a状态表示方程
经验+题目要求
有两种解题方式：
1、以某个位置为结尾。。。。。
假设dp[i][j]表示从期待您出发到达i，j位置数所需的最低健康点数
这个思路其实是错误的，因为你不仅需要进入这个房间，还要静茹下一个房间，这就导致了你不能简单的通过这个房间的前一步进行判断，还需要考虑后续房间的影响。————有后效性
2、以某个位置为起点。。。。。
dp[i][j]表示从这李出发到达终点所需最低初始健康。
b状态转移方程
根据最近的一步，划分问题
假设进入d[i][j]这个房间所需最小生命值为x
其实想要右边房间的话就需要：x+d[i][j]>=dp[i][j+1]
x>=dp[i][j+1]-d[i][j]
还有一种特殊情况需要我们考虑如果房间里面是一个较大血包的话，dp[i][j+1]-d[i][j]是有可能小于0的————这表示你就算是负多少多少都能够走到终点，但这是不合理的，负数骑士都死掉了。
所以
c初始化
虚拟节点（处理边界问题的好方法）
这道题需要考虑边界问题是最后一行和最后一列。
需要注意的两点：
1、设置合适的值，保证填表时值的正确性
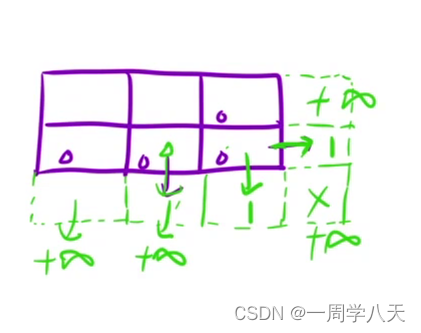
走出迷宫最少得剩下一滴血
2、注意下标映射
因为是添加在最后一行和最后一列，不需要考虑下标问题
d填表顺序
从下往上，从右往左
e返回值
dp[0][0]
3、代码
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {//建表//初始化//填表//返回值int m=dungeon.size(),n=dungeon[0].size();vector<vector<int>> dp(m+1,vector<int> (n+1,INT_MAX));dp[m][n-1]=1;dp[m-1][n]=1;for(int i=m-1;i>=0;i--){for(int j=n-1;j>=0;j--){int t=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];dp[i][j]=max(1,t);}}return dp[0][0];}
};
