UML的概念 

用例图的概念

• 包含 <<include>>
• 扩展<<exted>>
• 泛化

        用例图（也可称用例建模）描述的是外部执行者（Actor）所理解的系统功能。用例图用于需求分析阶段，它的建立是系统开发者和用户反复讨论的结果，表明了开发者和用户对需求规格达成的共识。
        在UML中，用例表示为一个椭圆。图显示了一个图书管理系统的用例图。其中，“新增书籍信息”、“查询书籍信息”、“修改书籍信息”、“登记外借情况”、“查询外借情况”、“统计金额与册数”等都是用例的实例。

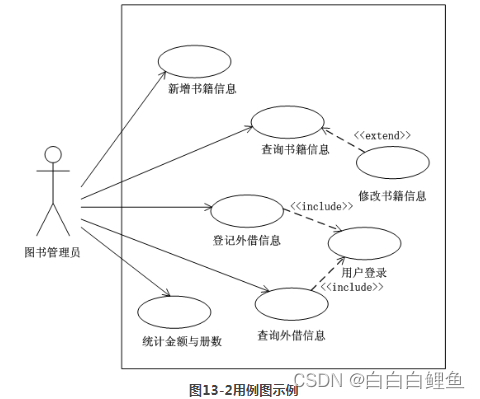
        用例分析技术为软件需求规格化提供了一个基本的元素，而且该元素是可验证、可度量的。用例可以作为项目计划、进度控制、测试等环节的基础。

泛化关系：

 聚合关系：

        聚合（Aggregation）是一种特殊形式的关联。聚合表示类之间的关系是整体与部分的关系。聚合关系的含义是“聚”在一起的意义，也就是表示“部分”可以独立于“整体”而存在。在UML模型中，使用一个带空心菱形的实线表示，空心菱形指向的是代表“整体”的类，如图13-10所示。

组合关系：

        如果发现“部分”类的存在，是完全依赖于“整体”类的，那么就应该使用“组合”关系来描述。在UML模型中，组合关系是使用带有实心菱形的实线表示，实心菱形指向的是代表“整体”的类。

聚合与组合的区别在什么地方呢？

        许多书籍虽然举过很多例子，但是都忽略了，这种例子是必须依赖于“应用场景”的。也就是要根据应用场景来判断部分类和整体类之间的关系。例如：“电脑”是一个整体类，而“主板”、“CPU”......则是相对于它的部分类。那么它们之间应该整体类还是部分类呢？如果你是在固定资产管理系统中，可能适合的就是“组合”，甚至只是“电脑”类的属性；而如果对于在线DIY的系统，那么显然应该采用“聚合”关系。对于组合而言，最易于理解的例子是“订单”与“订单项”之间的关系，如果订单不存在，显然订单项也就没有意义了，因此必然是组合关系。
原则：判断是聚合还是组合关系，关键在于要放到具体的应用场景中讨论。

实现关系：

类图 

• 依赖 
• 关联：聚合、组合
• 泛化 

        类关系图包含“依赖”“关联”“聚合”“组合”“实现”“继承”6种，从关系的紧密程度来看，从松到紧依次为：依赖<关联<聚合<组合<实现<继承。有趣的是，UML图中的连线貌似也体现了这种关系，简单来说，就是 虚线<实线，空心<实心 。

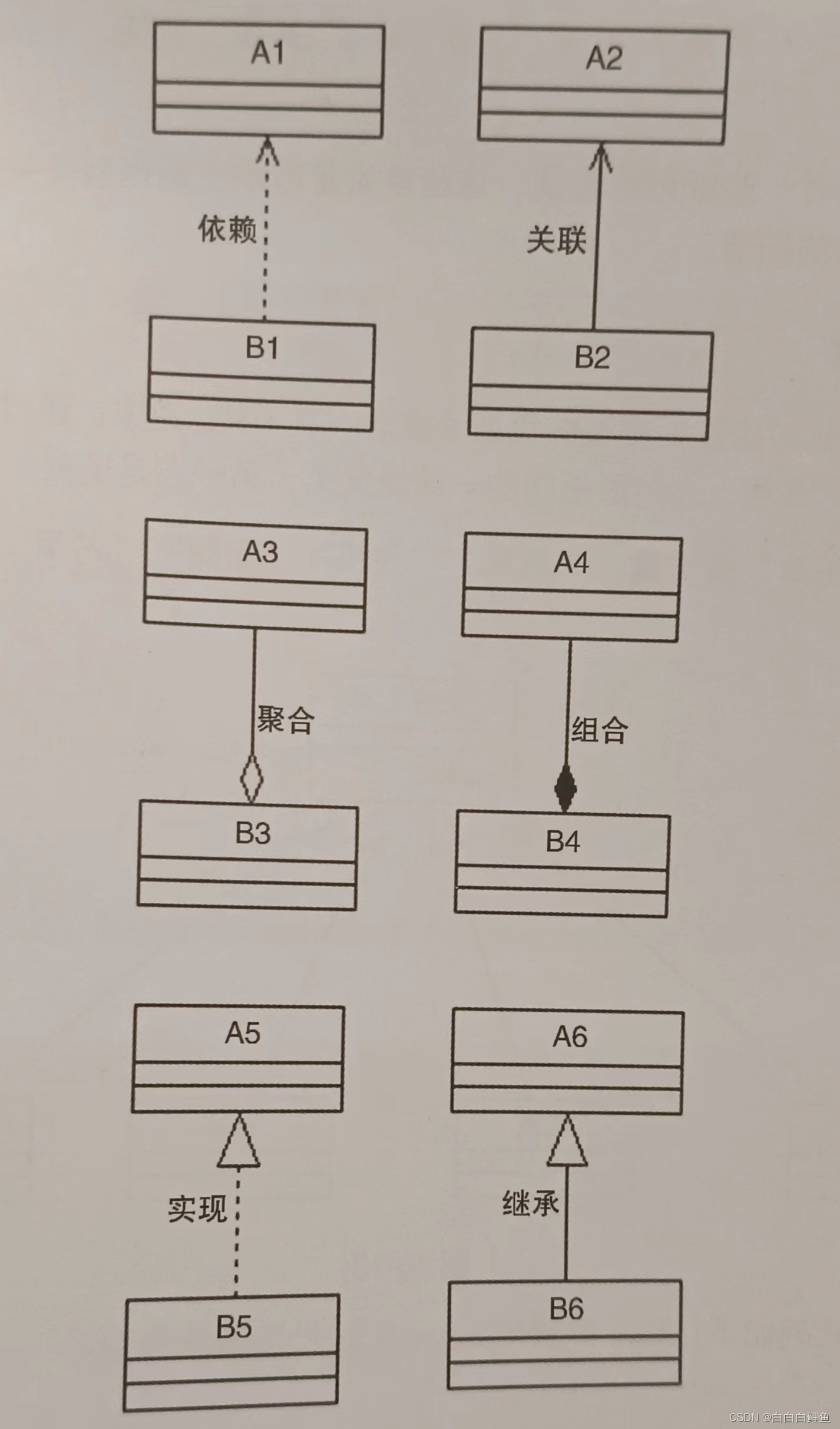
这6组关系按照关系的紧密程度又可以分为3组：

（1）使用关系：即B类调用了A类的方法或者使用了A类的属性，为了与下面的两组关系对应，也称为“use-a”关系，包括“依赖关系”和“关联关系”。
（2）包含关系：即B类和A类是“整体-部分”的关系，B类中包含A类，又叫“has-a"关系，包括“聚合关系”和“组合关系”。

（3）血缘关系：即B类属于A类，又叫“is-a”关系，包括“实现关系”和“继承关系”。