spring_01概念及案例

 

1.什么是IOC?　　

　　IOC概念:inverse of Controll,控制反转,所谓控制反转,就是把创建对象和维护对象关系的权利从程序中转移到spring的容器中(applicationContext.xml),而程序本身不再维护

 

2.什么是di?

　　dependency injection,依赖注入,di和IOC是一个概念,spring的设计者认为di等更能准确表达spring

 

3.学习框架,最主要的就是学习各个配置

 

4.spring层次图 

　　

 

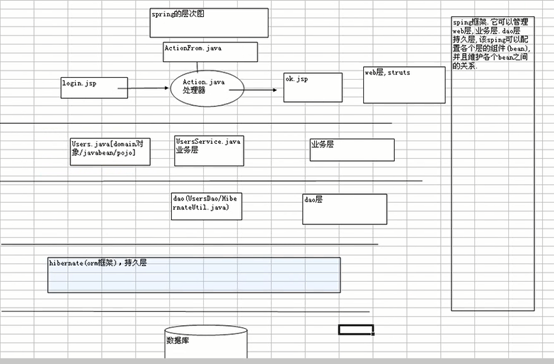
5.初次相遇spring,我的看法:

　　刚刚接触spring,素问spring是一个非常强大的框架,现在一看果然,他能够创建并管理几乎所有的bean对象,这里的bean对象包括:domain,dao,javabean,service...

　　它就像是一个工程师,协调各个框架(springMVC,struts,hibernate......),注入灵魂,从而创建出一个个伟大的项目,

 

6.搭建spring项目简单步骤:

　　1),导入jar包,spring.jar(这个包包含spring框架常用的包),common-logging.jar为日志包,前面两个包为必须,其余包按照需求选择导入

　　

　　2),在src目录下建立文件applicationContext.xml,一般都是在这个目录下配置,,并且名字为applicationContext.xml,部分开发人员也喜欢使用beans.xml这个名字

　　3),根据项目需要创建相关的类,并且配置到配置文件applicationContext.xml文件中,配置到配置文件中的类必须满足javabean类的规格

 

7.简单案例,对比使用传统方法和使用spring框架输出"hello,爱华顿g":

　　

package com.ahd.service;public class UserService {private String username;public String getUsername() {return username;}public void setUsername(String username) {this.username = username;}public void sayHello(){System.out.println("hello "+username);}
}

 

　　src目录下建立applicationContext.xml文件

<?xml version="1.0" encoding="UTF-8"?><beans xmlns="http://www.springframework.org/schema/beans"xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xmlns:context="http://www.springframework.org/schema/context"xmlns:tx="http://www.springframework.org/schema/tx"xsi:schemaLocation="http://www.springframework.org/schema/beans http://www.springframework.org/schema/beans/spring-beans-2.5.xsdhttp://www.springframework.org/schema/context http://www.springframework.org/schema/context/spring-context-2.5.xsdhttp://www.springframework.org/schema/tx http://www.springframework.org/schema/tx/spring-tx-2.5.xsd"><!-- 在容器文件中配置数据源(bean/entity/service/dao/pojo) --><!-- bean元素的作用是当spring框架加载的时候,spring会自动为bean类 UserService类的属性设置值  id就是创建对象的对象名 --><bean id="userService" class="com.ahd.service.UserService">
<!—name对应java类中的属性,value是赋值--!><property name="username"><value>爱华顿g</value></property></bean>
</beans>

 

　　测试类Test

package com.ahd.test;import static org.junit.Assert.*;import com.ahd.service.UserService;public class Test {@org.junit.Testpublic void test() {//不使用spring框架,使用传统编程方法//1.创建对象UserService userService=new UserService();//2.设置属性userService.setUsername("爱华顿g");//3.调用方法
        userService.sayHello();}@org.junit.Testpublic void test1(){//使用spring来完成上面的流程//1.得到spring的容器对象ApplicationContextApplicationContext ac=new ClassPathXmlApplicationContext("applicationContext.xml");//2.获取bean对象UserService us=(UserService) ac.getBean("userService");//3.调用方法us.sayHello();}
}

 

　　结果截图: