深度网络概览

[hide]

1 概述
2 深度网络的优势
3 训练深度网络的困难
- 3.1 数据获取问题
- 3.2 局部极值问题
- 3.3 梯度弥散问题
4 逐层贪婪训练方法
- 4.1 数据获取
- 4.2 更好的局部极值
5 中英文对照
6 中文译者

概述

在之前的章节中，你已经构建了一个包括输入层、隐藏层以及输出层的三层神经网络。虽然该网络对于MNIST手写数字数据库非常有效，但是它还是一个非常“浅”的网络。这里的“浅”指的是特征（隐藏层的激活值 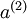$\textstyle {a}^{(2)}$ ）只使用一层计算单元（隐藏层）来得到的。

在本节中，我们开始讨论深度神经网络，即含有多个隐藏层的神经网络。通过引入深度网络，我们可以计算更多复杂的输入特征。因为每一个隐藏层可以对上一层的输出进行非线性变换，因此深度神经网络拥有比“浅层”网络更加优异的表达能力（例如可以学习到更加复杂的函数关系）。

值得注意的是当训练深度网络的时候，每一层隐层应该使用非线性的激活函数 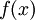$\textstyle f(x)$ 。这是因为多层的线性函数组合在一起本质上也只有线性函数的表达能力（例如，将多个线性方程组合在一起仅仅产生另一个线性方程）。因此，在激活函数是线性的情况下，相比于单隐藏层神经网络，包含多隐藏层的深度网络并没有增加表达能力。

深度网络的优势

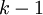为什么我们要使用深度网络呢？使用深度网络最主要的优势在于，它能以更加紧凑简洁的方式来表达比浅层网络大得多的函数集合。正式点说，我们可以找到一些函数，这些函数可以用 $\textstyle k$ 层网络简洁地表达出来（这里的简洁是指隐层单元的数目只需与输入单元数目呈多项式关系）。但是对于一个只有 $\textstyle k-1$ 层的网络而言，除非它使用与输入单元数目呈指数关系的隐层单元数目，否则不能简洁表达这些函数。

举一个简单的例子，比如我们打算构建一个布尔网络来计算 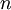$\textstyle n$ 个输入比特的奇偶校验码（或者进行异或运算）。假设网络中的每一个节点都可以进行逻辑“或”运算（或者“与非”运算），亦或者逻辑“与”运算。如果我们拥有一个仅仅由一个输入层、一个隐层以及一个输出层构成的网络，那么该奇偶校验函数所需要的节点数目与输入层的规模 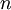$\textstyle n$ 呈指数关系。但是，如果我们构建一个更深点的网络，那么这个网络的规模就可做到仅仅是 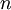$\textstyle n$ 的多项式函数。

当处理对象是图像时，我们能够使用深度网络学习到“部分-整体”的分解关系。例如，第一层可以学习如何将图像中的像素组合在一起来检测边缘（正如我们在前面的练习中做的那样）。第二层可以将边缘组合起来检测更长的轮廓或者简单的“目标的部件”。在更深的层次上，可以将这些轮廓进一步组合起来以检测更为复杂的特征。

最后要提的一点是，大脑皮层同样是分多层进行计算的。例如视觉图像在人脑中是分多个阶段进行处理的，首先是进入大脑皮层的“V1”区，然后紧跟着进入大脑皮层“V2”区，以此类推。

训练深度网络的困难

虽然几十年前人们就发现了深度网络在理论上的简洁性和较强的表达能力，但是直到最近，研究者们也没有在训练深度网络方面取得多少进步。问题原因在于研究者们主要使用的学习算法是：首先随机初始化深度网络的权重，然后使用有监督的目标函数在有标签的训练集 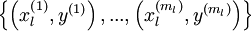$\textstyle \left\{ \left( x_{l}^{\left( 1 \right)},{{y}^{\left( 1 \right)}} \right),...,\left( x_{l}^{\left( {{m}_{l}} \right)},{{y}^{\left( {{m}_{l}} \right)}} \right) \right\}$ 上进行训练。例如通过使用梯度下降法来降低训练误差。然而，这种方法通常不是十分奏效。这其中有如下几方面原因：

数据获取问题

使用上面提到的方法，我们需要依赖于有标签的数据才能进行训练。然而有标签的数据通常是稀缺的，因此对于许多问题，我们很难获得足够多的样本来拟合一个复杂模型的参数。例如，考虑到深度网络具有强大的表达能力，在不充足的数据上进行训练将会导致过拟合。

局部极值问题

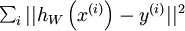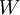使用监督学习方法来对浅层网络（只有一个隐藏层）进行训练通常能够使参数收敛到合理的范围内。但是当用这种方法来训练深度网络的时候，并不能取得很好的效果。特别的，使用监督学习方法训练神经网络时，通常会涉及到求解一个高度非凸的优化问题（例如最小化训练误差 $\textstyle \sum\nolimits_{i}{||{{h}_{W}}\left( {{x}^{\left( i \right)}} \right)-{{y}^{\left( i \right)}}|{{|}^{2}}}$ ，其中参数 $\textstyle W$ 是要优化的参数。对深度网络而言，这种非凸优化问题的搜索区域中充斥着大量“坏”的局部极值，因而使用梯度下降法（或者像共轭梯度下降法，L-BFGS等方法）效果并不好。

梯度弥散问题

梯度下降法（以及相关的L-BFGS算法等）在使用随机初始化权重的深度网络上效果不好的技术原因是：梯度会变得非常小。具体而言，当使用反向传播方法计算导数的时候，随着网络的深度的增加，反向传播的梯度（从输出层到网络的最初几层）的幅度值会急剧地减小。结果就造成了整体的损失函数相对于最初几层的权重的导数非常小。这样，当使用梯度下降法的时候，最初几层的权重变化非常缓慢，以至于它们不能够从样本中进行有效的学习。这种问题通常被称为“梯度的弥散”.

与梯度弥散问题紧密相关的问题是：当神经网络中的最后几层含有足够数量神经元的时候，可能单独这几层就足以对有标签数据进行建模，而不用最初几层的帮助。因此，对所有层都使用随机初始化的方法训练得到的整个网络的性能将会与训练得到的浅层网络（仅由深度网络的最后几层组成的浅层网络）的性能相似。

逐层贪婪训练方法

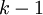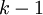那么，我们应该如何训练深度网络呢？逐层贪婪训练方法是取得一定成功的一种方法。我们会在后面的章节中详细阐述这种方法的细节。简单来说，逐层贪婪算法的主要思路是每次只训练网络中的一层，即我们首先训练一个只含一个隐藏层的网络，仅当这层网络训练结束之后才开始训练一个有两个隐藏层的网络，以此类推。在每一步中，我们把已经训练好的前 $\textstyle k-1$ 层固定，然后增加第 $\textstyle k$ 层（也就是将我们已经训练好的前 $\textstyle k-1$ 的输出作为输入）。每一层的训练可以是有监督的（例如，将每一步的分类误差作为目标函数），但更通常使用无监督方法（例如自动编码器，我们会在后边的章节中给出细节）。这些各层单独训练所得到的权重被用来初始化最终（或者说全部）的深度网络的权重，然后对整个网络进行“微调”（即把所有层放在一起来优化有标签训练集上的训练误差）.

逐层贪婪的训练方法取得成功要归功于以下几方面：

数据获取

虽然获取有标签数据的代价是昂贵的，但获取大量的无标签数据是容易的。自学习方法（self-taught learning）的潜力在于它能通过使用大量的无标签数据来学习到更好的模型。具体而言，该方法使用无标签数据来学习得到所有层（不包括用于预测标签的最终分类层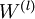） $\textstyle {{W}^{\left( l \right)}}$ 的最佳初始权重。相比纯监督学习方法，这种自学习方法能够利用多得多的数据，并且能够学习和发现数据中存在的模式。因此该方法通常能够提高分类器的性能。