自我学习
今天让我们来完成自我学习的代码。完成这个代码需要结合稀疏自编码和softmax分类器,具体的可以看我以前的博客。
依赖
- MNIST Dataset
- Support functions for loading MNIST in Matlab
- Starter Code (stl_exercise.zip)
这需要有MNIST的数据,这部分代码已经在文件里面自带。
第二步:训练相应的自编码器
我们将使用无标签数据(从5到9)来训练一个稀疏自编码,使用sparseAutoencoderCost.m,来完成相应的操作。这个在前面的博客里面的我已经完成了。完成这一步,我的电脑差不多跑了将近40分钟。
我们仅需要对stlExercise.m里面加入相应的代码(Step 2里面)
%% ----------------- YOUR CODE HERE ----------------------
% Find opttheta by running the sparse autoencoder on
% unlabeledTrainingImagesopttheta = theta; options.Method = 'lbfgs'; % Here, we use L-BFGS to optimize our cost% function. Generally, for minFunc to work, you% need a function pointer with two outputs: the% function value and the gradient. In our problem,% sparseAutoencoderCost.m satisfies this.
options.MaxIter = 400; % Maximum number of iterations of L-BFGS to run
options.Display = 'iter';
options.GradObj = 'on';[opttheta, cost] = fminlbfgs( @(p) sparseAutoencoderCost(p, ...inputSize, hiddenSize, ...lambda, sparsityParam, ...beta, unlabeledData), ...theta, options);% save('min_func_result.mat', 'trainSet', 'testSet', 'unlabeledData', 'trainData', 'trainLabels', 'testData', 'testLabels', 'opttheta');% load('min_func_result.mat');最终会得到下面的结果

第3步:导出特征
在稀疏自编码后,我们将导出特征。我们得完成feedForwardAutoEncoder.m里面的代码。
这步我们得自己来写。
function [activation] = feedForwardAutoencoder(theta, hiddenSize, visibleSize, data)% theta: trained weights from the autoencoder
% visibleSize: the number of input units (probably 64)
% hiddenSize: the number of hidden units (probably 25)
% data: Our matrix containing the training data as columns. So, data(:,i) is the i-th training example. % We first convert theta to the (W1, W2, b1, b2) matrix/vector format, so that this
% follows the notation convention of the lecture notes. W1 = reshape(theta(1:hiddenSize*visibleSize), hiddenSize, visibleSize);
b1 = theta(2*hiddenSize*visibleSize+1:2*hiddenSize*visibleSize+hiddenSize);%% ---------- YOUR CODE HERE --------------------------------------
% Instructions: Compute the activation of the hidden layer for the Sparse Autoencoder.
m=size(data,2);
z_2=W1*data+repmat(b1,1,m);
a_2=sigmoid(z_2);
activation=a_2;%-------------------------------------------------------------------end%-------------------------------------------------------------------
% Here's an implementation of the sigmoid function, which you may find useful
% in your computation of the costs and the gradients. This inputs a (row or
% column) vector (say (z1, z2, z3)) and returns (f(z1), f(z2), f(z3)). function sigm = sigmoid(x)sigm = 1 ./ (1 + exp(-x));
end
我们得通过先前写的代码softmaxTrain.m来完成相应的功能。
我们在stlExercise.m文件里面的第4步改成相应的
%% ----------------- YOUR CODE HERE ----------------------
% Use softmaxTrain.m from the previous exercise to train a multi-class
% classifier. % Use lambda = 1e-4 for the weight regularization for softmax% You need to compute softmaxModel using softmaxTrain on trainFeatures and
% trainLabelslambda = 1e-4;
numClasses = numel(unique(trainLabels));softmaxModel = softmaxTrain(hiddenSize, numClasses, lambda, ...trainFeatures, trainLabels, options);我们可以运行程序,看看输出的结果。
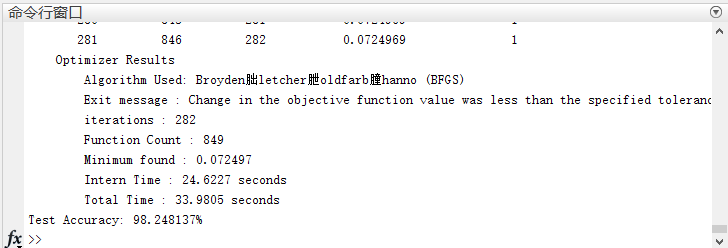
我们可以看到最后的精度还是挺高的,相比较之下,原始数据的精度只有96%。
)
)

)

)


)


cv2.rotate)


开箱点评)




