从自我学习到深层网络
在前一节中,我们利用自编码器来学习输入至 softmax 或 logistic 回归分类器的特征。这些特征仅利用未标注数据学习获得。在本节中,我们描述如何利用已标注数据进行微调,从而进一步优化这些特征。如果有大量已标注数据,通过微调就可以显著提升分类器的性能。
在自我学习中,我们首先利用未标注数据训练一个稀疏自编码器。随后,给定一个新样本  ,我们通过隐含层提取出特征
,我们通过隐含层提取出特征 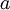 。上述过程图示如下:
。上述过程图示如下:
我们感兴趣的是分类问题,目标是预测样本的类别标号 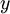 。我们拥有标注数据集
。我们拥有标注数据集 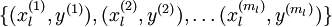 ,包含
,包含 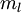 个标注样本。此前我们已经说明,可以利用稀疏自编码器获得的特征
个标注样本。此前我们已经说明,可以利用稀疏自编码器获得的特征 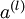 来替代原始特征。这样就可获得训练数据集
来替代原始特征。这样就可获得训练数据集 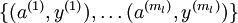 。最终,我们训练出一个从特征
。最终,我们训练出一个从特征 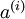 到类标号
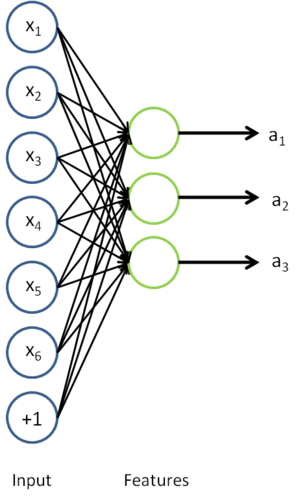
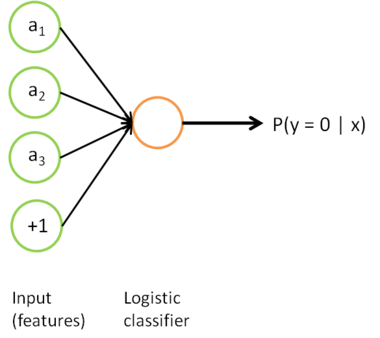
到类标号 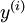 的 logistic 分类器。为说明这一过程,我们按照神经网络一节中的方式,用下图描述 logistic 回归单元(橘黄色)。
的 logistic 分类器。为说明这一过程,我们按照神经网络一节中的方式,用下图描述 logistic 回归单元(橘黄色)。
考虑利用这个方法所学到的分类器(输入-输出映射)。它描述了一个把测试样本  映射到预测值
映射到预测值 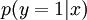 的函数。将此前的两张图片结合起来,就得到该函数的图形表示。也即,最终的分类器可以表示为:
的函数。将此前的两张图片结合起来,就得到该函数的图形表示。也即,最终的分类器可以表示为:
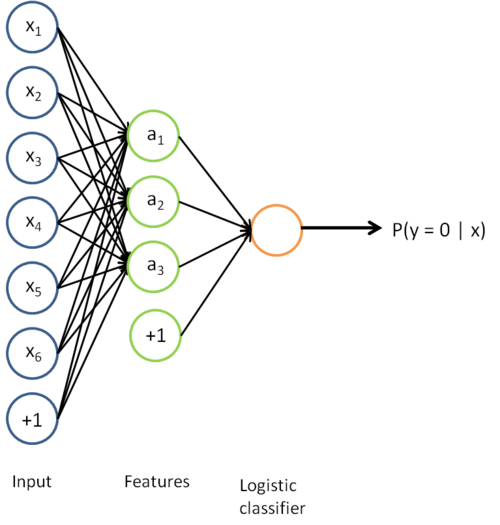
该模型的参数通过两个步骤训练获得:在该网络的第一层,将输入  映射至隐藏单元激活量
映射至隐藏单元激活量 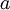 的权值
的权值 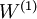 可以通过稀疏自编码器训练过程获得。在第二层,将隐藏单元
可以通过稀疏自编码器训练过程获得。在第二层,将隐藏单元 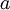 映射至输出
映射至输出 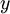 的权值
的权值 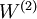 可以通过 logistic 回归或 softmax 回归训练获得。
可以通过 logistic 回归或 softmax 回归训练获得。
这个最终分类器整体上显然是一个大的神经网络。因此,在训练获得模型最初参数(利用自动编码器训练第一层,利用 logistic/softmax 回归训练第二层)之后,我们可以进一步修正模型参数,进而降低训练误差。具体来说,我们可以对参数进行微调,在现有参数的基础上采用梯度下降或者 L-BFGS 来降低已标注样本集 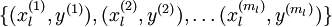 上的训练误差。
上的训练误差。
使用微调时,初始的非监督特征学习步骤(也就是自动编码器和logistic分类器训练)有时候被称为预训练。微调的作用在于,已标注数据集也可以用来修正权值 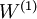 ,这样可以对隐藏单元所提取的特征
,这样可以对隐藏单元所提取的特征 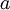 做进一步调整。
做进一步调整。
到现在为止,我们描述上述过程时,都假设采用了“替代 (Replacement)”表示而不是“级联 (Concatenation)”表示。在替代表示中,logistic 分类器所看到的训练样本格式为 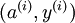 ;而在级联表示中,分类器所看到的训练样本格式为
;而在级联表示中,分类器所看到的训练样本格式为 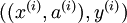 。对级联表示同样可以进行微调(在级联表示神经网络中,输入值
。对级联表示同样可以进行微调(在级联表示神经网络中,输入值 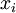 也直接被输入至 logistic 分类器。对此前的神经网络示意图稍加更改,即可获得其示意图。具体的说,第一层的输入节点除了与隐层联接之外,还将越过隐层,与第三层输出节点直接相连)。但是对于微调来说,级联表示相对于替代表示几乎没有优势。因此,如果需要开展微调,我们通常使用替代表示的网络(但是如果不开展微调,级联表示的效果有时候会好得多)。
也直接被输入至 logistic 分类器。对此前的神经网络示意图稍加更改,即可获得其示意图。具体的说,第一层的输入节点除了与隐层联接之外,还将越过隐层,与第三层输出节点直接相连)。但是对于微调来说,级联表示相对于替代表示几乎没有优势。因此,如果需要开展微调,我们通常使用替代表示的网络(但是如果不开展微调,级联表示的效果有时候会好得多)。
在什么时候应用微调?通常仅在有大量已标注训练数据的情况下使用。在这样的情况下,微调能显著提升分类器性能。然而,如果有大量未标注数据集(用于非监督特征学习/预训练),却只有相对较少的已标注训练集,微调的作用非常有限。
中英文对照
- 自我学习 self-taught learning
- 深层网络 deep networks
- 微调 fine-tune
- 稀疏自编码器 sparse autoencoder
- 梯度下降 gradient descent
- 非监督特征学习 unsupervised feature learning
- 预训练 pre-training
)

)


)


cv2.rotate)


开箱点评)





)
)
