目录
一、特征统计量
1.概率分布
2.特征统计量
二、平稳时间序列的定义
严平稳与宽平稳的关系
三、平稳时间序列的统计性
四、平稳性的重大意义
五、平稳性检验
时序图检验
自相关图检验
R绘图
一、特征统计量
平稳性是某些时间序列具有的一种统计特征要描述清楚这个特征,我们必须借助以下统计工具。
1.概率分布
时间序列概率分布族:
![]()
实际应用的局限性
2.特征统计量
- 均值
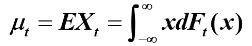
- 方差
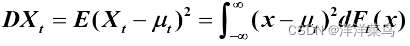
- 自协方差
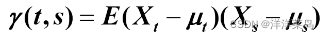
- 自相关系数(ρ)
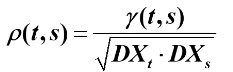
二、平稳时间序列的定义
- 严平稳:随机变量族的统计性质完全有它们的联合概率分布族决定,若任意的t下的联合概率分布族相等,则认为该序列是严平稳的
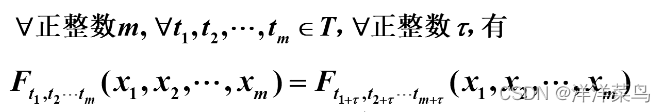
宽平稳:(使用序列的特征统计量来定义)认为序列的统计性质主要由它的低阶矩决定,所以只要保证序列低阶矩平稳(二阶),就能保证序列的主要性质近似稳定:
满足如下条件的序列可称为宽平稳序列 :
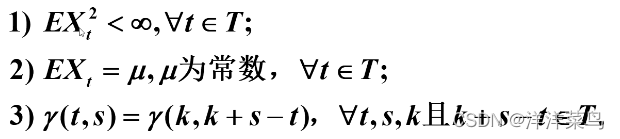
严平稳与宽平稳的关系
- 一般关系

- 特例

三、平稳时间序列的统计性
1)均值为常数:Ex=μ(μ为常数)2)自协方差和自相关系数只依赖于时间的平移长度而与时间的起止点无关
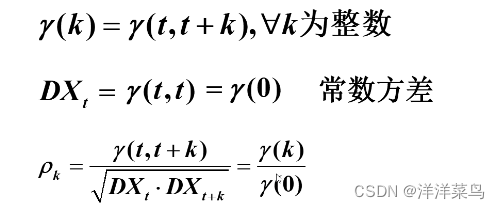
自相关系数的4个性质:规范性、对称性、非负定性和非唯一性

- 非唯一性:一个平稳时间序列一定唯一决定它的自相关函数,一个自相关函数未必唯一对应一个平稳时间序列
四、平稳性的重大意义
- 在平稳序列场合,均值序列变成了只含有一个常量的常数序列。
{ut,t属于T} ——> {u,t属于T}
- 原本每个随机变量的均值(方差,自相关系数)只能依靠唯一的一个样本观察值去估计,瞎子你由于平稳性,每个统计量都将拥有大量的样本观察值。
- 这极大地减少了随机变量的个数,并增加了待估变量的样本容量。极大地简化了时序分析的难度,同时也提高了对特征统计量的估计精度。
五、平稳性检验
- 图检验:
- 时序图 ——> 优点:操作简便
- 自相关图 ——> 缺点:结论带有一定的主观色彩
- 假设检验:单位根检验
-
时序图检验
根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终再一个常数值附近波动,而且波动的范围有界、无明显趋势及周期特征
如果有趋势或周期,通常是非平稳
-
自相关图检验
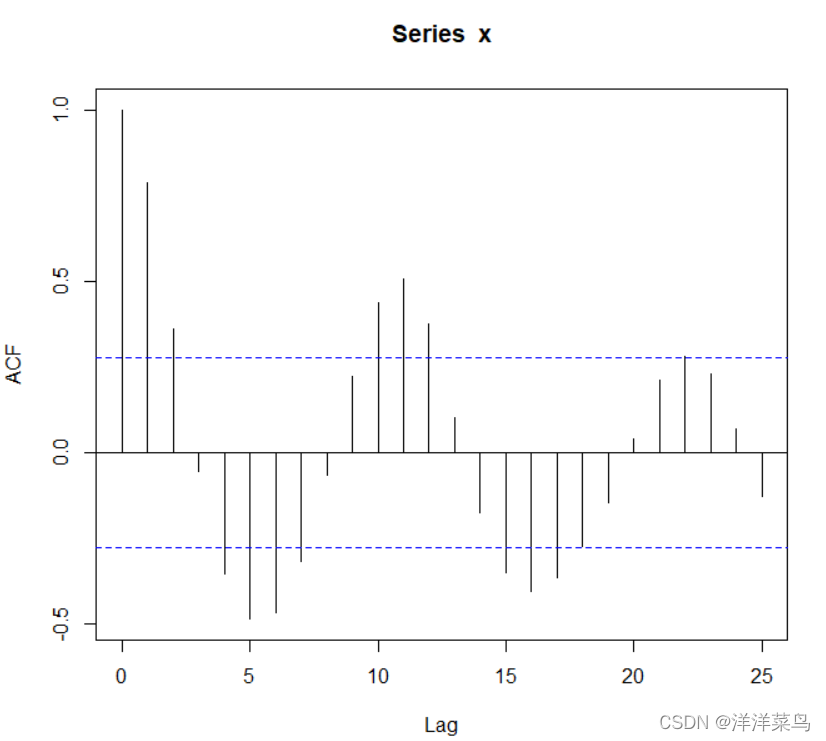
平稳序列通常具有短期相关性。该性质用自相关系数来描述就是随着延迟期数的增加,平稳序列的自相关系数会很快地衰减向零。
非平稳序列衰减向零地速度通常比较慢。
R绘图
在R中,绘制时序图可用plot()函数,绘制自相关图可用acf()函数
在后续会详细介绍相关绘图的参数,其相关的数据也会在后续上传。
我们先看一下例2_1,在这里截取部分数据
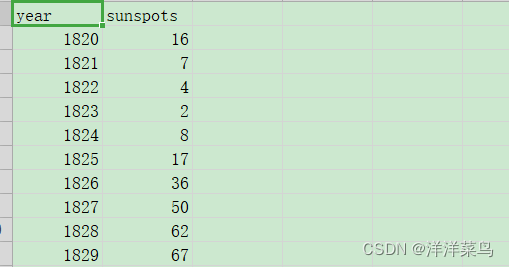
在这里我们可以看到,数据有标题,且都是每年一个数据
代码如下:
读取数据时 要用 / 或者 \\ ,否则会出错
a<-read.table("D:/桌面/E2_1.csv")
a返回:

然后我们进行时间序列分离变量时会报错,
如执行代码:x<-ts(a$sunspots,start=1964)
错误如下:

那么该如何解决?
这时就应该回到最初读取数据时了,如下
a<-read.table("D:/桌面/E2_1.csv",sep=",",header=T)
a此时读取如下:

可以发现,第一列和第二列已经完全分开了,嘿嘿,我们接下来在进行下一步
x<-ts(a$sunspots,start=1964)
x在这里,a$是为了选出x所代表的数据,start表示数据的起始时间,原数据的起始时间是1820,在这里我们用的1964,对结果不会有影响,就是所对应的时间会有所改变
结果如下:

接下来,我们进行一下绘图试试
先画个时序图:
plot(x)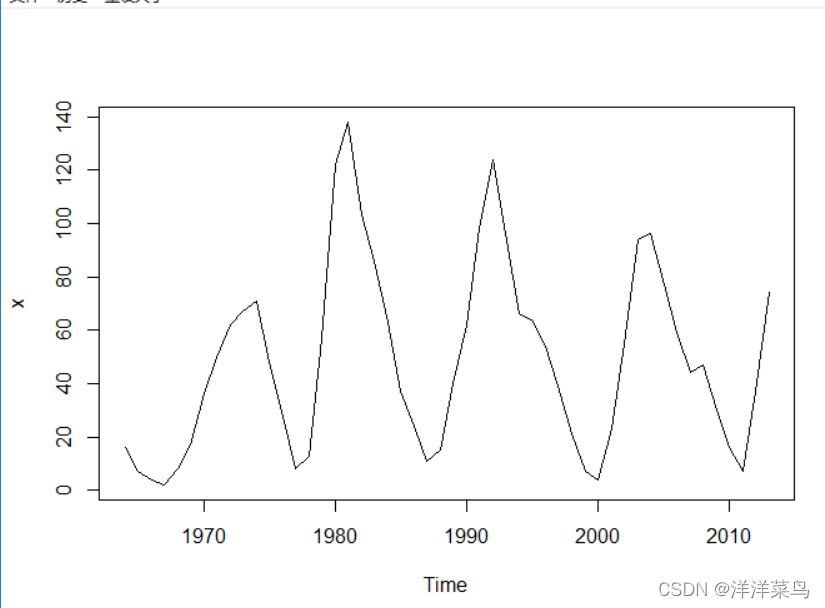
再画个自相关图:
acf(x,lag.max=25)lag.max 也可以用 lag 代替哦

返回结果为:
接下来,我们再举一个例子2-2
读取方法跟上面一样,不再多讲了
a<-read.table("D:/桌面/E2_2.csv",sep=",",header=T)
返回结果:
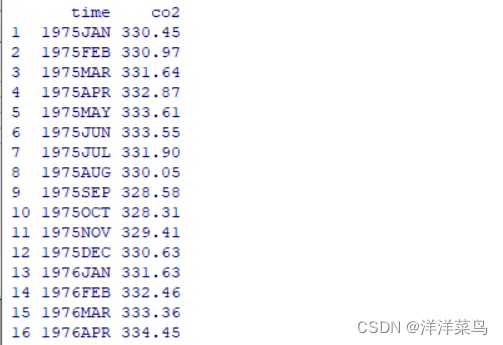
仔细看看可知,它们是一年12个月都有的哦
接下来的分离数据就有所不同了,方法如下:
x<-ts(a$co2,start=c(1975,1),frequency=12)
xfrequency 代表频率,这里表示一年有12个月,如果是4个季度就是4
返回结果如下:
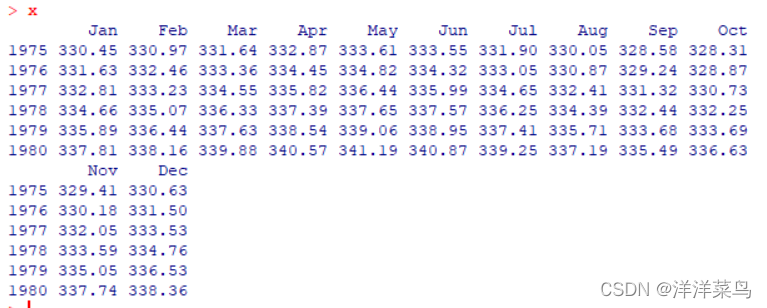
绘制时序图:
plot(x)
返回:
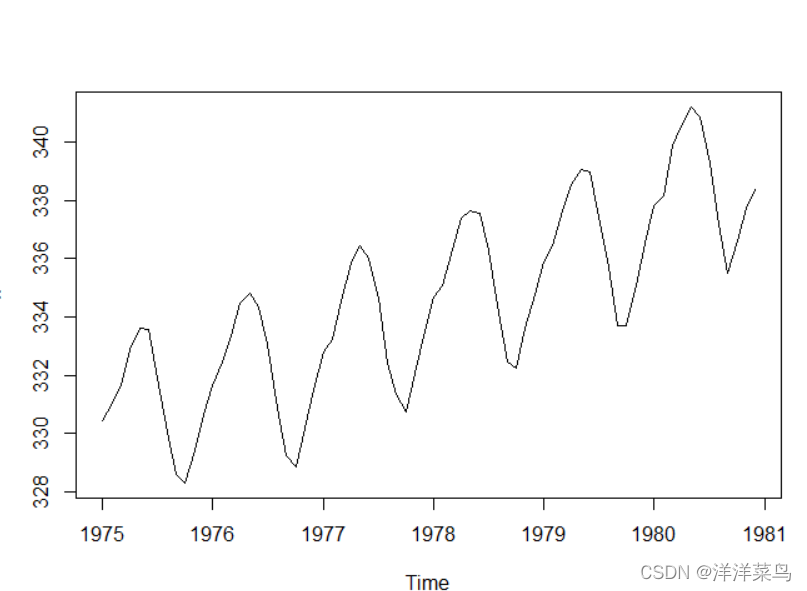
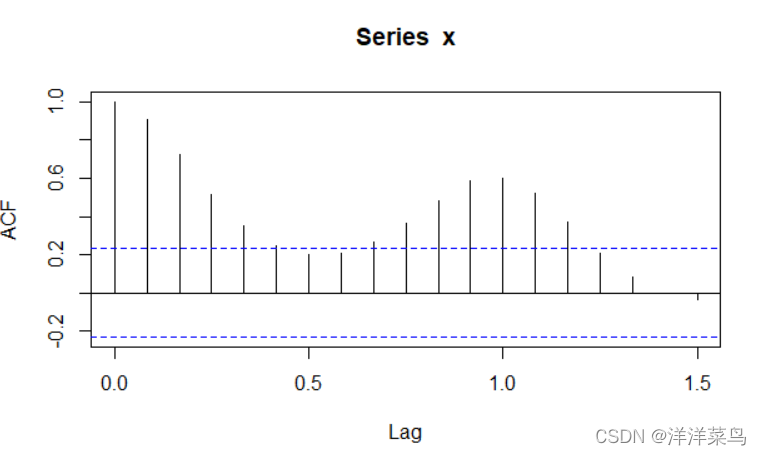
绘制自相关图:
acf(x)返回:
这次,我们介绍到这里,如有问题,欢迎评论区见哦!!
















)
)

