目录

        1.纯随机序列的定义

2.性质

3.纯随机性检验

---

1.纯随机序列的定义

• 纯随机序列也称为白噪声序列，满足如下性质：

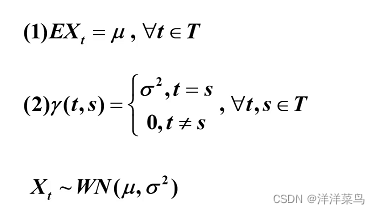
2.性质

• 纯随机性（无记忆性）

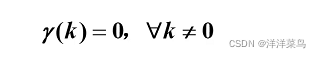
•  方差齐性

举例，随机生成1000个白噪声序列

用正态分布序列 rnorm(数量，均值，方差)，如下为，1000个标准正态的分布图形

a<-rnorm(1000)
x<-ts(a)
plot(x)

时序图如下：

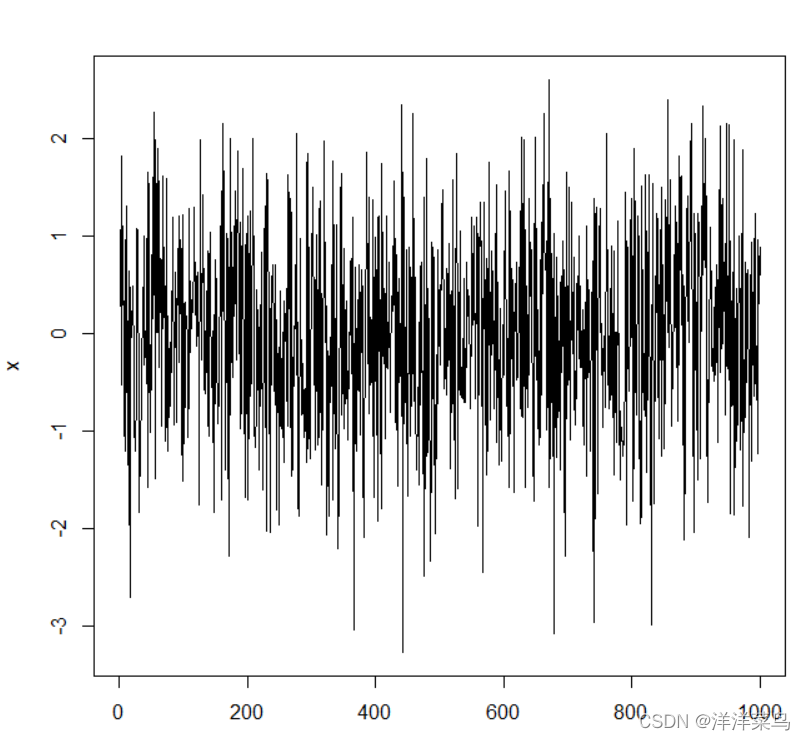
 自相关图：

acf(x)

返回：

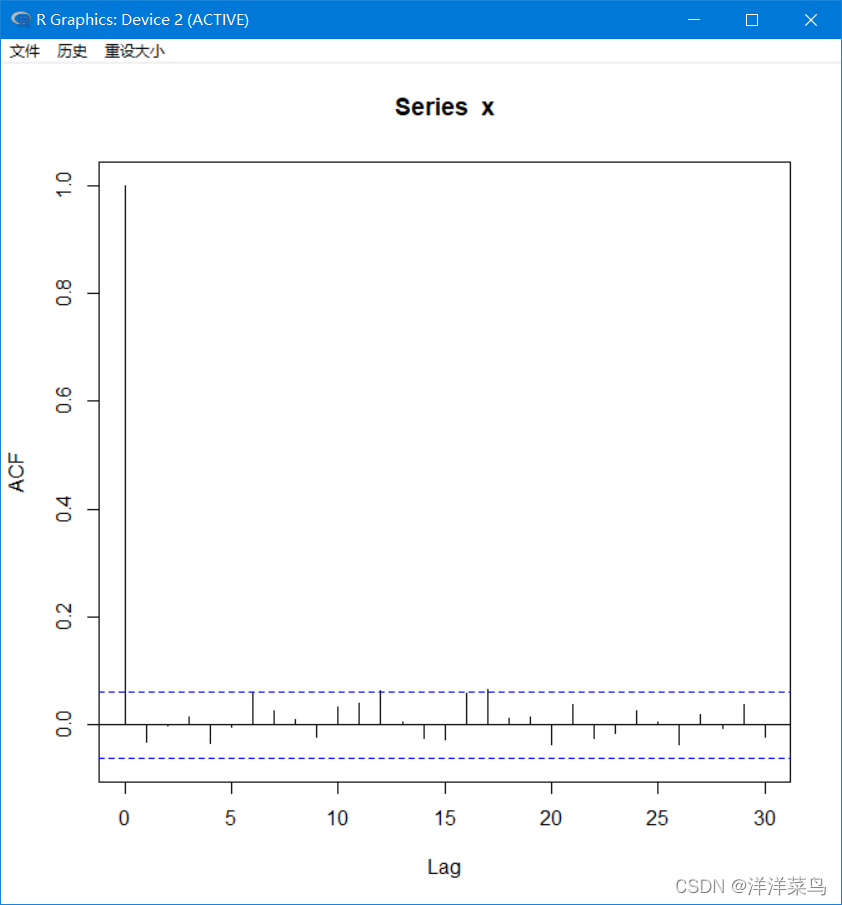
如图，可以看出自相关系数基本分布在二倍标准差之间，但由于数据是随机的，所以有一定的误差

3.纯随机性检验

Bartlett定理：如果一个时间序列是纯随机的，得到一个观察期数为n的观察序列，那么该序列的延迟非零期的样本自相关系数将近似服从均值为0，方差为序列观察期数倒数的正态分布

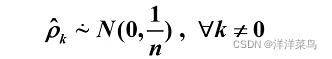
原假设：

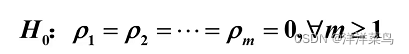
备择假设：

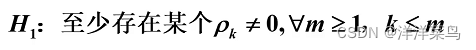
Q统计量（Box和Pierce）：服从自由度为m的卡方分布，其对大样本检验效果较好

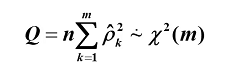
LB统计量（Box和Ljung）：Q统计量的修正，现在使用较普遍

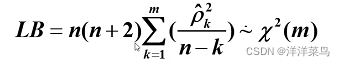
拒绝域：

R语言白噪声检验

Box.test(x,type=,lag=6)  
其中：
type='Box-Pierce'  Q统计量 ，默认
type='Ljung-Box'   LB统计量

举例1：对上面随机生成的白噪声序列进行6阶和12阶的LB统计量

for(i in 1:2)print( Box.test(x,type='Ljung-Box',lag=6*i))

返回：

举例2：对1900年到1998年全球7级以上地震法伤次数序列进行平稳性和纯随机性检验

读取数据

a<-read.table('D:/桌面/E2_5.csv',sep=',',header=T)
a

返回：

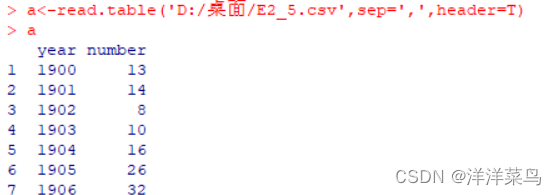
 选择变量序列

x<-ts(a$number,start=1900)
x

返回：

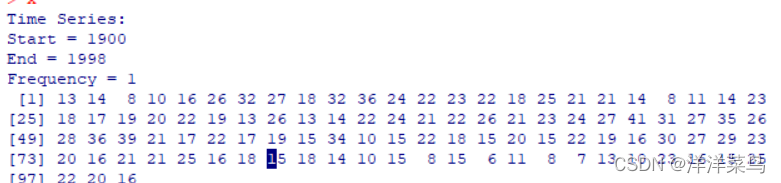
绘制时序图：

plot(x)

绘制自相关图： 

acf(x)

6阶LB统计量：

Box.test(x,type='Ljung-Box',lag=6)

返回：