目录

1.wold分解定理（1938）

2.AR模型

2.1定义：

 AR(p) 有三个限制条件：

中心化 AR(p) 模型

2.2 AR模型的平稳性判别

序列拟合函数

R 举例

---

1.wold分解定理（1938）

对于任何一个离散平稳序列 {xt} 他都可以分解为两个不相关的平稳序列之和，其中一个为确定性的，另一个为随机性的，不妨记作

其中：

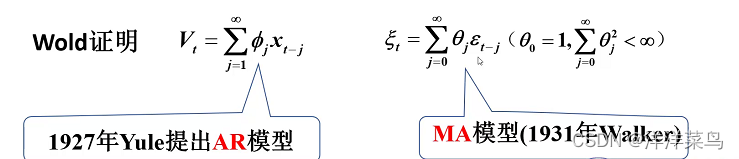
2.AR模型

2.1定义：

如下结构的模型称为P阶自回归（autoregression）模型，简记为 AR(p)

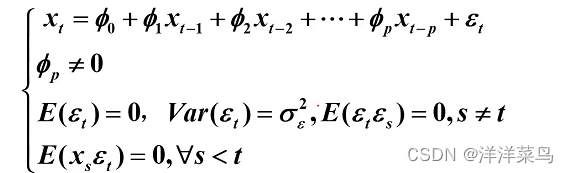
 AR(p) 有三个限制条件：

        条件1：

         这个限制条件保证了模型的最高阶数为 p

        条件2：

         这个限制条件实际上是要求随机干扰序列{t}为零均值白噪声序列

        条件3：

         这个限制条件说明当期的随机干扰与过去的序列值无关

通常会缺省上面的限制条件，把 AR(p) 模型简记为：

中心化 AR(p) 模型

则中心化 AR(p) 模型 为：

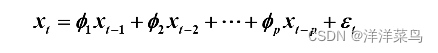
引入延迟算子，可记为：

 又可简记为：

则可得到p阶子回归系数多项式

2.2 AR模型的平稳性判别

AR模型是常用的平稳序列的拟合模型之一，但并非所有的AR模型都是平稳的

序列拟合函数

1.arima.sim函数拟合

只能拟合平稳的数据

2. filter 函数拟合

可拟合非平稳的数据

R 举例

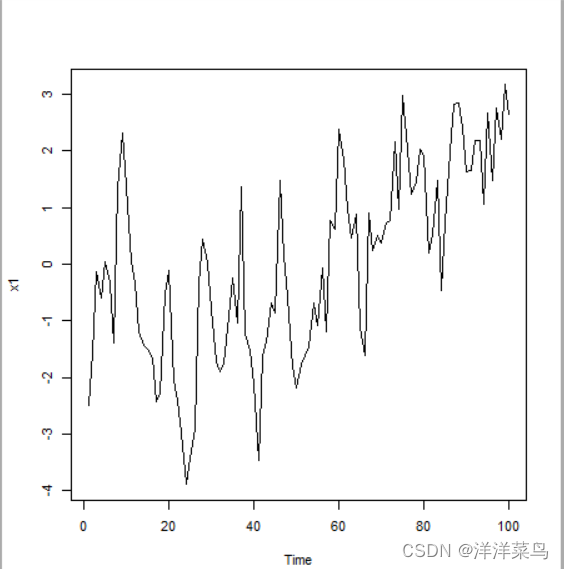
例1：平稳序列

x1<-arima.sim(n=100,list(ar=0.8))
plot(x1)

 返回：

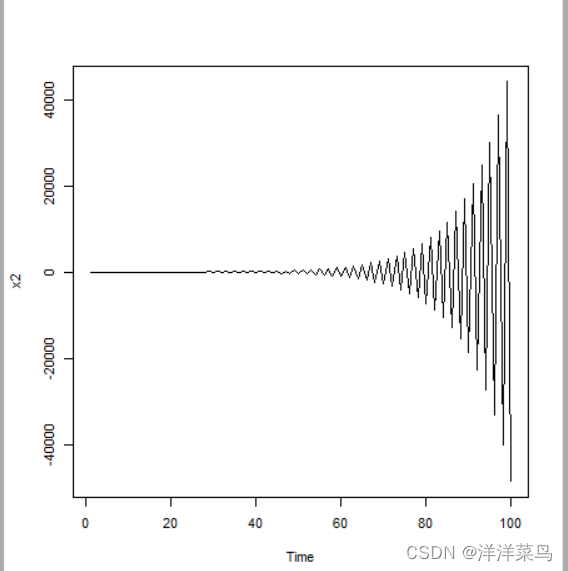
例2：非平稳序列

x2<-arima.sim(n=100,list(ar=-1.1))

返回：

我们发现报错，报错提示，该不是平稳序列，所以我们应改为用filter 函数拟合，如下

x2<-filter(rnorm(100),filter=-1.1,method="recursive")
plot(x2)

返回：

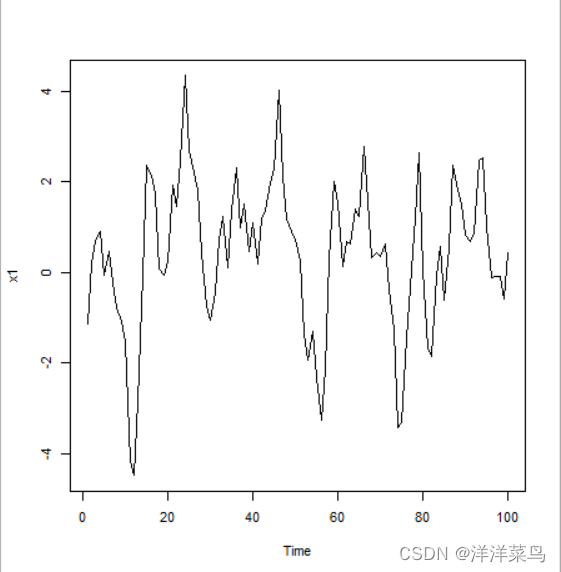
例3：平稳序列

x1<-arima.sim(n=100,list(ar=c(1,-0.5)))
plot(x1)

返回：

例4：非平稳序列

这个就不在这写了，大家可以自己用这个试试哦，看看是否你已经掌握了。