目录
1.特征根判别法
AR(p)模型对应齐次方程特征根与回归系数多项式根的关系:
2.平稳域判别
(1)AR(1)(一阶)模型平稳域
(2)AR(2)(二阶)模型平稳域
3.举例
4.函数展开成幂级数——麦克劳林级数
小结
1.特征根判别法
AR模型可以看作非齐次差分方程,它的解不妨记作
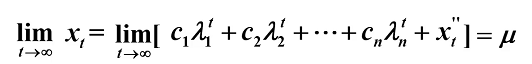
平稳条件:|| < 1
- AR模型平稳 <——> 特征根都在单位圆内
AR(p)模型对应齐次方程特征根与回归系数多项式根的关系:
中心化AR(p)模型:
![]()
对应齐次方程的特征方程:
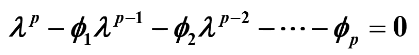
自回归系数多项式:
![]()
我们令 得:
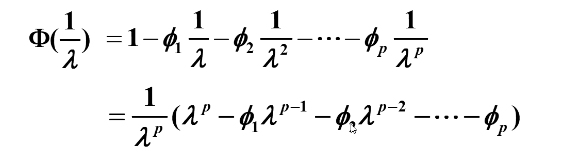
令上式等于 0 ,可知,根为倒数关系。
2.平稳域判别
AR(p)模型
![]()
平稳 <——> { | 特征根都在单位圆内}
对于低阶自回归模型通常更为简便。
(1)AR(1)(一阶)模型平稳域
模型:
![]()
特征方程:
![]()
特征根:
![]()
(2)AR(2)(二阶)模型平稳域
模型:
![]()
特征方程:
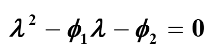
特征根:
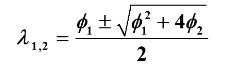
平稳域:
平稳域的条件有:
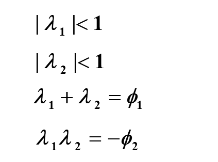
由上述条件我们可以推导如下:
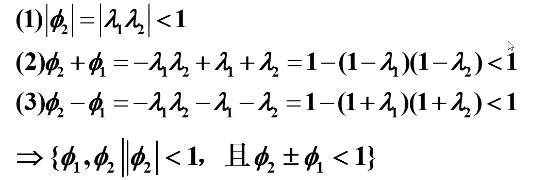
再把上述平稳域可视化,如下
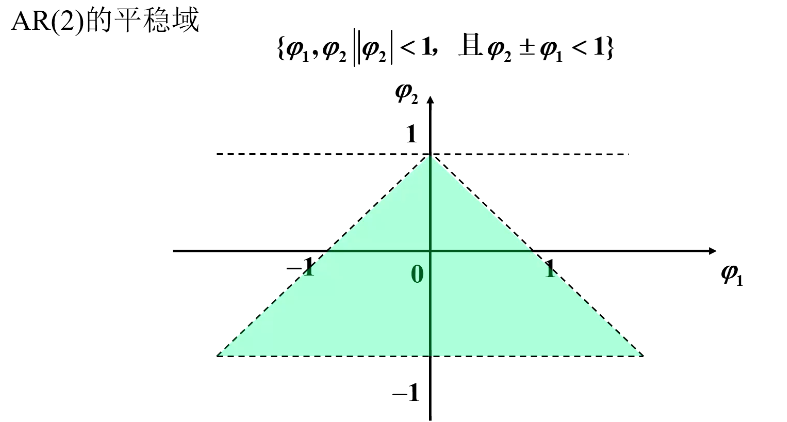
3.举例
例子仍为上篇文章中的例子:传送门
在上一篇文章,我们用R通过绘图,知道了它们是否为平稳性,接下来我们通过特征根和平稳域来判别一下它们的平稳性
第一个:一阶平稳
![]()
特征根判别:
因为 - 0.8 = 0 ,所以得到
= 0.8 。又因为|
| < 1,所以 平稳。
平稳域判别:
可知,,因为
,所以平稳
第二个:一阶非平稳
![]()
特征根判别:
因为 - (-1.1)= 0 ,所以得到
= 1.1 。又因为|
| <>1,所以 非平稳。
平稳域判别:
可知,,因为
,所以 非平稳
第三个:二阶平稳
![]()
特征根判别:
解的:
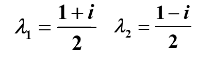
又因为 模(长度) ,所以 平稳
平稳域判别:
所以平稳
第四个:二阶非平稳
![]()
特征根判别:
解得:
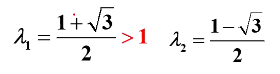
因为 不在单位圆内,所以 非平稳
平稳域判别:
>1
4.函数展开成幂级数——麦克劳林级数
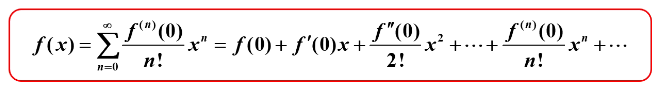
如:
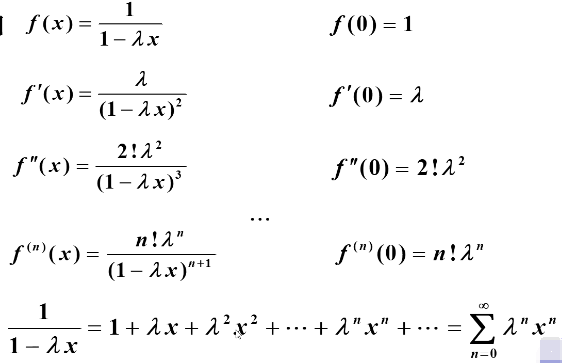
小结
1.
AR(p)模型 :
![]()
可简记为:
![]()
p阶自回归系数多项式 :
![]()
2. 平稳性判定
单位根 特征根都在单位圆内
平稳域
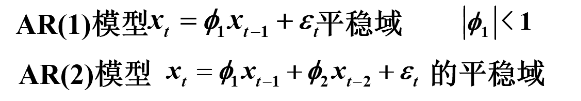
3.函数展开成幂级数——麦克劳林级数
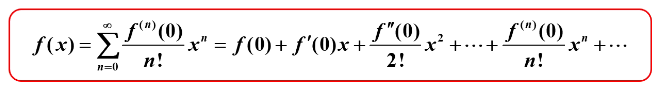
)


)详解 —— python)


)详解 —— matlab)












