目录
一、差分 Xt
二、延迟算子
延迟算子的性质
p阶差分
k步差分
三、线性差分方程
齐次线性差分方程的解
非齐次线性差分方程的解
时序分析与线性差分方程的关系
一、差分 Xt
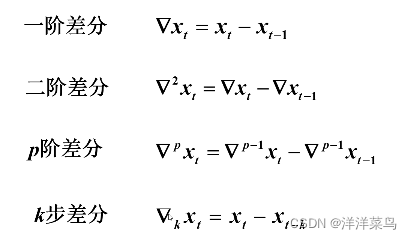
二、延迟算子
- 延迟算子类似于一个时间指针，当前序列值乘以一个延迟算子，就相当于把当前序列值的时间向过去拨了一个时刻
- 记B为延迟算子，有
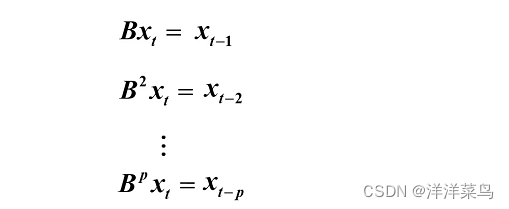
延迟算子的性质
用延迟算子表示差分运算
p阶差分
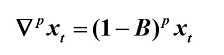
计算方式：
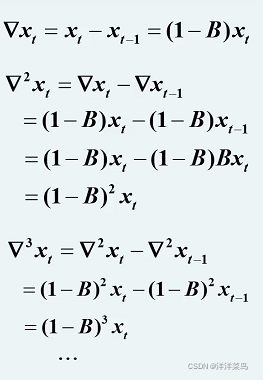
k步差分
三、线性差分方程
齐次线性差分方程的解
齐次线性差分方程（ h(t)=0 ）
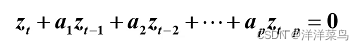
先找到特征方程
特征根可以记作为
则有：
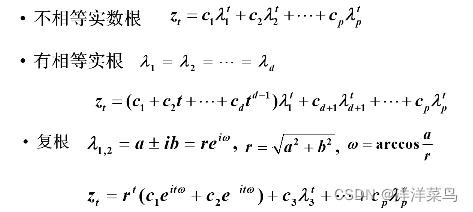
非齐次线性差分方程的解
非齐次线性差分方程的特解：
- 使得非齐次线性差分方程成立的任意一个解
非齐次线性差分方程的通解：
- 齐次线性差分方程的通解Z't 和 非齐次线性差分方程的特解 Z''t 之和
时序分析与线性差分方程的关系
- 常用的时间序列模型和某些模型的自协方差函数和自相关函数都可以视为线性差分方程
- 线性差分方程队以ing的特征根的性质对判断模型的平稳性有着非常重要的意义
