总结

空间中不共线的两个不为零向量都可以表示空间中的任意一个向量。但是这种向量太多了，我们选一个特殊点的，i=[1 0]和j=[0 1]作为单位向量，i和j的拉伸与相加可以组成笛卡尔坐标系中的任意一个向量。给定向量（基）线性组合的向量的集合，被称为给定向量（基）张成的空间。第三个向量u落在前两个向量v和w张成的空间中。那这些向量线性相关，也就是说向量没有给张成的空间增加新的维度。如果向量线性无关，比如w张成的空间是一维的，向量v不落在w张成的空间中，那么v和w张成的空间就变成了二维平面，向量给张成的空间增加了新的维度。可见向量空间的一组基，是张成该空间的线性无关向量的集合。变换也就相当于函数：接收内容，输出结果。对于线性变换，可以理解为直线在变换后仍然保持为直线，不能有所弯曲，而且原点必须保持固定。可以用矩阵描述线性变换，将变换后的基向量坐标分别写到矩阵的每一列。一个v向量乘以矩阵，可以得到变换后的v，而且可以根据变换后的i和j推断出来v的位置。如果说两个矩阵相乘，那么也就是进行了一次复合变换。线性变换将空间拉伸或挤压，想要测量变换对空间有多少拉伸或挤压，那么我们就可以求矩阵的行列式，也就是线性变换改变面积的比例。矩阵的列，是基向量变换后的位置，变换后，基向量张成的空间，就是所有可能的变换结果。经过一个变换，空间被压缩到低维，就导致一系列向量变换后成为零向量。变换后落在原点的向量的集合叫做矩阵的零空间。秩也就是变换后空间的维度，也就是矩阵的列张成的空间的维度。空间中同一个向量可以用不同语言描述，区别就在于坐标系选取的不同。坐标描述，依赖于所选的基向量。如果说使用不同的基向量描述同一个东西，描述的形式是不同的。那么如何在不同坐标系之间进行转化？可以用笛卡尔坐标系的语言表达别的坐标系的的基向量。以笛卡尔坐标系语言描述的别的坐标系的基向量作为列，形成一个基变换矩阵。通过这个矩阵，可以将别的坐标系语言描述的向量，转换成笛卡尔坐标系语言描述的向量。一个线性变换作用于一个向量，大部分向量在变换中都离开了它原来张成的空间，但还有一些特殊的向量仍然留在他们张成的空间里，这意味着矩阵对它的作用仅仅是拉伸或压缩，这些特殊向量就被称为变换的特征向量，特征值也就是特征向量在变换中拉伸或压缩的比例。如果变换有许多特征向量，多到能张成全空间，那就可以变换坐标系，使这些特征向量就是基向量。在另一个坐标系中表达当前坐标系描述的变换：首先通过基变换矩阵，用我们的语言描述另一个坐标系中的基向量，然后左乘线性变换矩阵，用我们的语言描述线性变换，然后再左乘基变换矩阵的逆，得到用另一个坐标系语言描述的线性变换。最终得到的变换是从新基向量所构成的坐标系角度看的。特征向量作为基向量的到的新的矩阵是对角的，并且对角元为对应的特征值，因为它所处坐标系的基向量在变换中只进行了缩放。

线性代数远不止这些空间中直观的运用，在模糊控制领域，同样用到了矩阵，只不过那里面矩阵的运算变成了取交集、并集。空间中理解线性代数是片面的，但有助于更好的认知。

向量

数学角度：

向量可以是任何东西，只需要保证：两个向量相加及数字与向量相乘是有意义的即可。

物理角度：

向量是空间中的箭头、决定一个向量的是：它的长度和它所指的方向。

计算机角度：

向量是有序的数字列表、向量的维度等于“列表”的长度。

坐标系：

把向量至于坐标系中，坐标正负表示方向，原点为起点，可完美把两个不同的角度融合

向量加法：

物理：首尾相连 Motion

计算机：坐标相加。
向量乘法：

物理：缩放 Scaling

计算机：坐标和比例相乘。

函数也是向量:
$$\begin{gathered} (f+g)(x)=f(x)+g(x) \\ (2f)(x)=2f(x) \end{gathered}$$
函数相加、相乘和向量对应坐标相加、相乘很相似，只不过它有无穷多个坐标要相加、相乘。

函数的线性变换：
$$\frac{d}{dx}L(\frac{1}{9}{x}^3)=\frac{1}{3}{x}^2-1$$
线性的定义：满足以下两条性质。
$$\begin{gathered} L(\vec{v}+\vec{w})=L(\vec{v})+L(\vec{w}) \\ L(c\vec{v})=cL(\vec{v}) \end{gathered}$$
用矩阵表示求导：

当前空间：全体多项式。

给空间赋予坐标含义，取一个基：取x的不同次幂作为基函数，基函数集无穷大。

怎么构建变换矩阵：

求每一个基函数的导数，把结果放在对应列。

向量空间：

让所有已经建立好的理论和概念适用于一个向量空间，必须满足八条公理。

线性组合

空间中不共线的两个不为零向量都可以表示空间中的任意一个向量。
$$a\vec{\mathbf{v}}+b\vec{\mathbf{w}}$$
线性：如果你固定其中一个标量，让另一个标量自由变化，所产生的向量终点会描出一条直线。

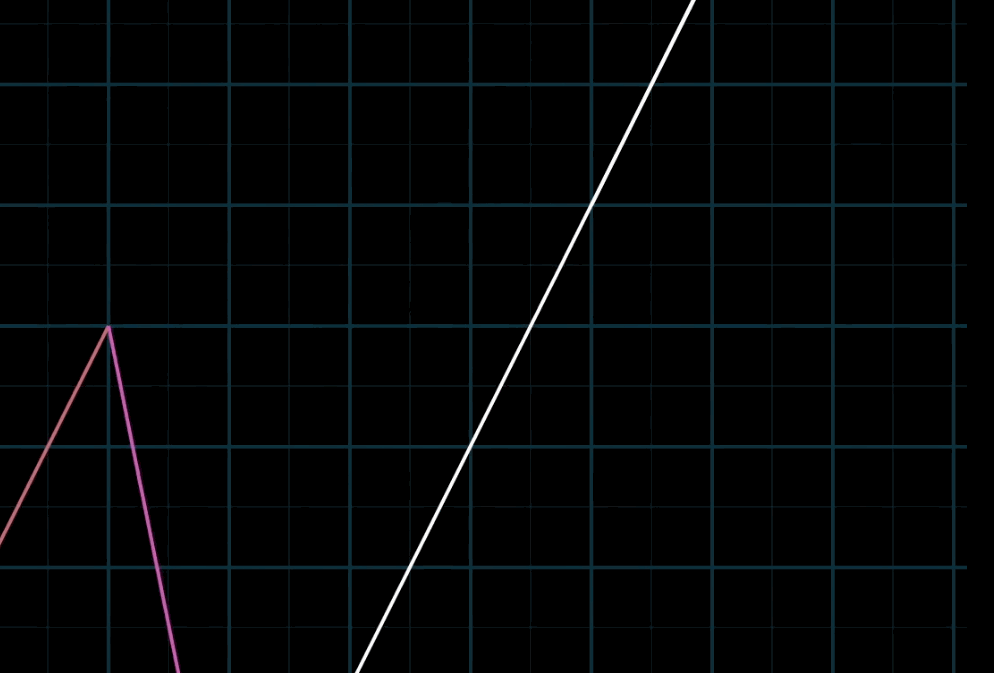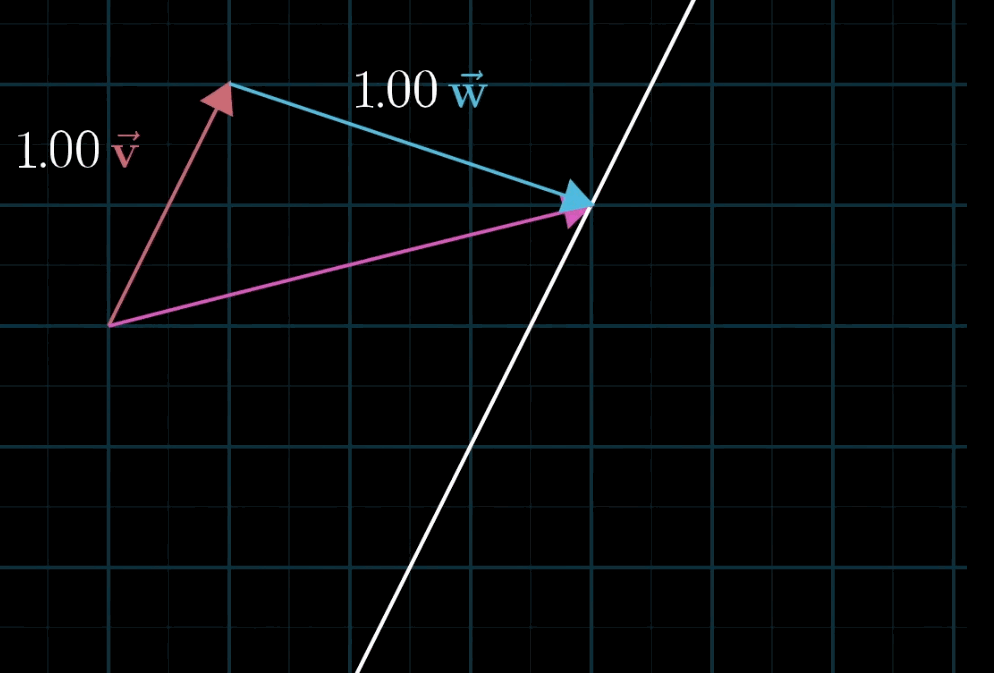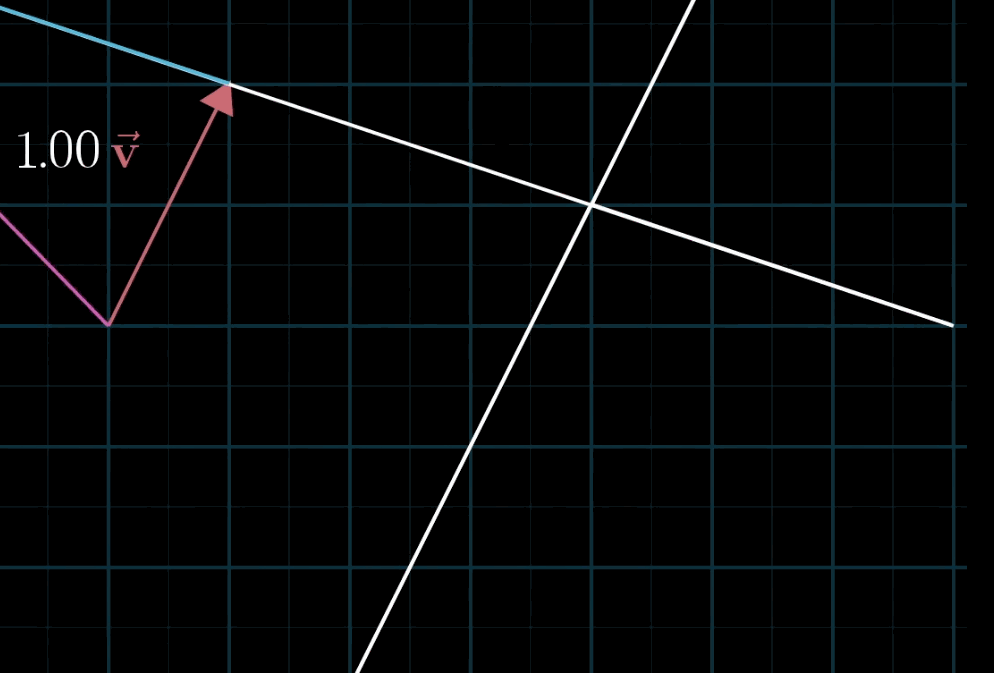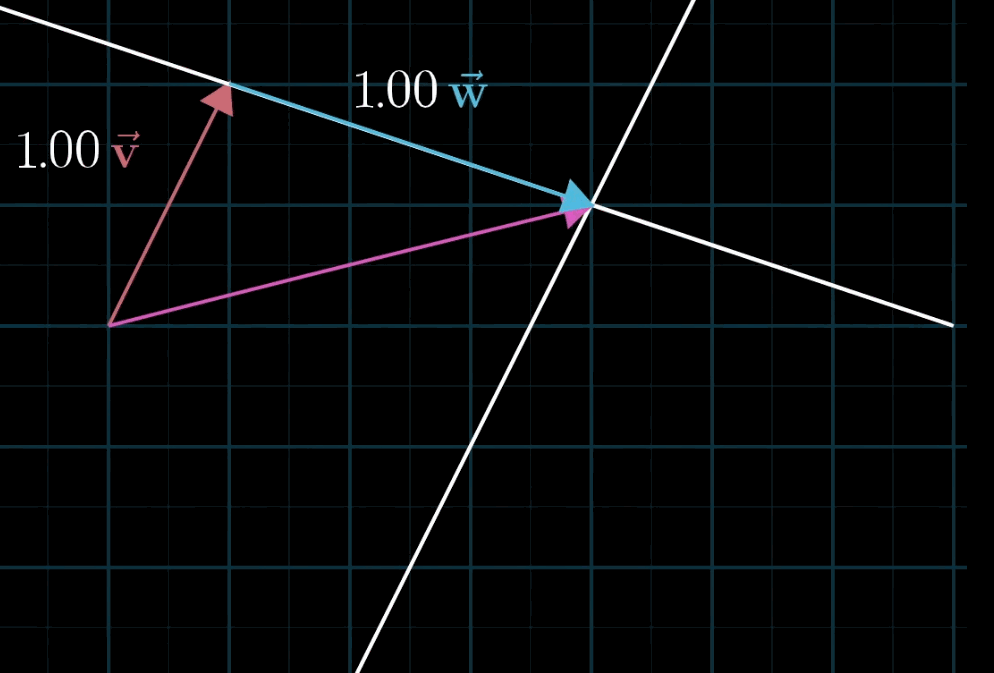
空间的基 Basis

笛卡尔坐标系，有一个最直观一组基：
{ı^,ȷ^}\{{\hat {\imath}} ,{\hat {\jmath}} \} {ı^,ȷ^​}
即单位向量：
$$\hat{ı}=(1,0)$$

$$\hat{ȷ}=(0,1)$$

通过i和j的拉伸与相加可以组成笛卡尔坐标系中的任意一个向量。

张成的空间 Span

给定向量（基）线性组合的向量的集合，被称为给定向量（基）张成的空间。

举个例子：v与w全部线性组合构成的向量集合，叫做张成的空间。(a与b在实数范围内变动)
$$a\vec{\mathbf{v}}+b\vec{\mathbf{w}}$$
仅通过向量加法和向量数乘两种计算，能获得所有可能向量的集合。

线性相关和线性无关

举个例子：

第三个向量u落在前两个向量v和w张成的空间中。那这些向量线性相关。
$$\vec{\mathbf{u}}=a\vec{\mathbf{v}}+b\vec{\mathbf{w}}$$

如果说，向量给张成的空间增加了新的维度，那这些向量线性无关。

举个例子：

w张成的空间是一维的。

向量v不落在w张成的空间中，那么v和w张成的空间就变成了二维平面。
$$\begin{gathered} \vec{\mathbf{v}}\ne b\vec{\mathbf{w}} \\ a\vec{\mathbf{v}}+b\vec{\mathbf{w}} \end{gathered}$$

向量空间的一组基

向量空间的一组基，是张成该空间的 线性无关向量 的集合。

变换

变换也就相当于函数：接收内容，输出结果

线性变换

直线在变换后仍然保持为直线，不能有所弯曲。

原点必须保持固定。

保持网格线平行且等距分布的变换。

数值描述线性变换

如果i和j没有进行变换，那么v也没有变换。
$$\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}x\\ y\end{array}\right]$$

绿色代表i变换后的向量，红色代表j变换后的向量。

可以根据变换后的i和j推断变换后的v。
$$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\underset{\text{直观的部分这里}}{\underbrace{x\left[\begin{array}{c}a\\ c\end{array}\right]+y\left[\begin{array}{c}b\\ d\end{array}\right]}}=\left[\begin{array}{c}ax+by\\ cx+dy\end{array}\right]$$

矩阵，一种描述线性变换的语言。

复合变换

对一个向量先进行一次旋转变换，再进行一次剪切变换。

求一个复合矩阵，

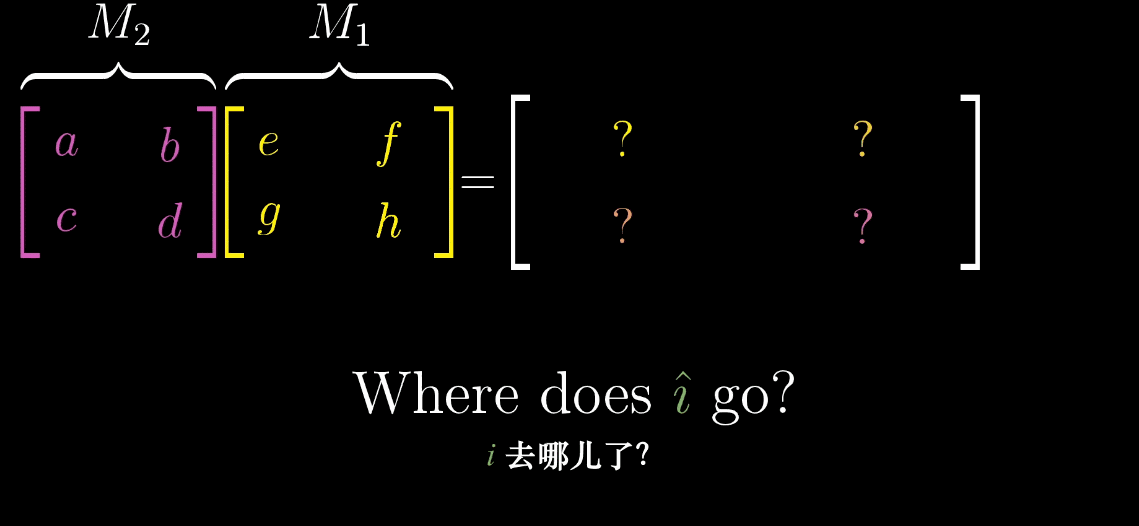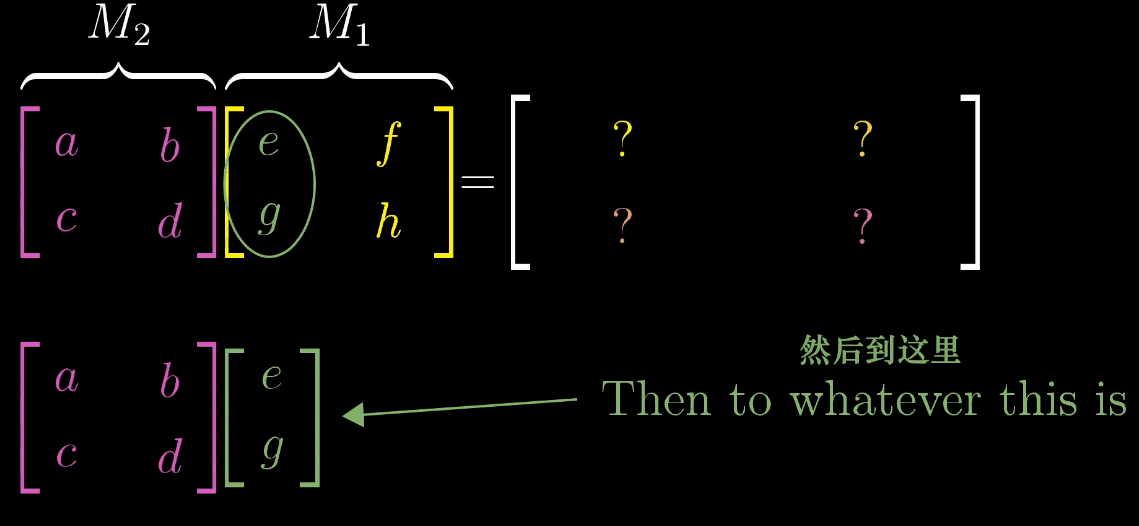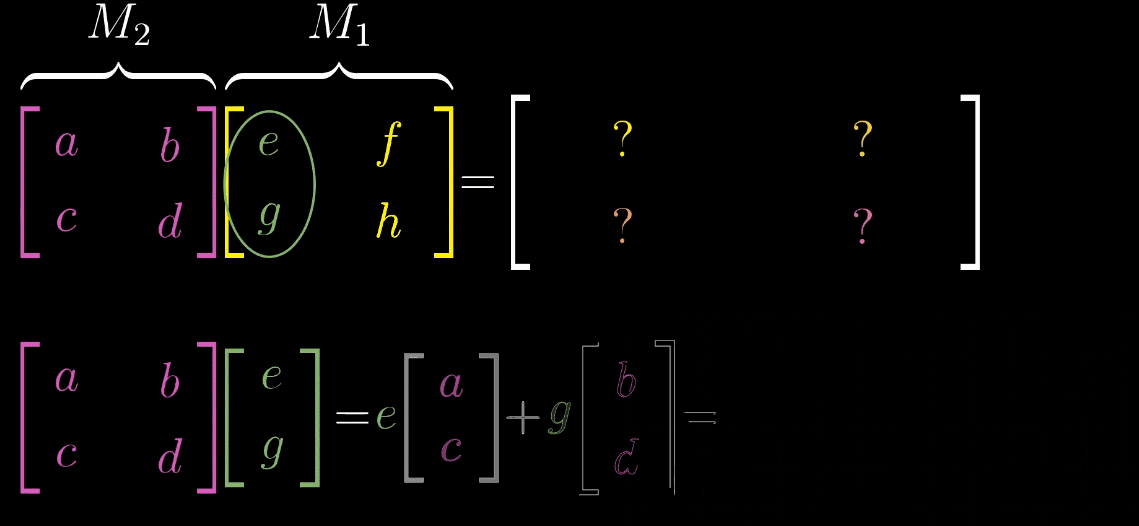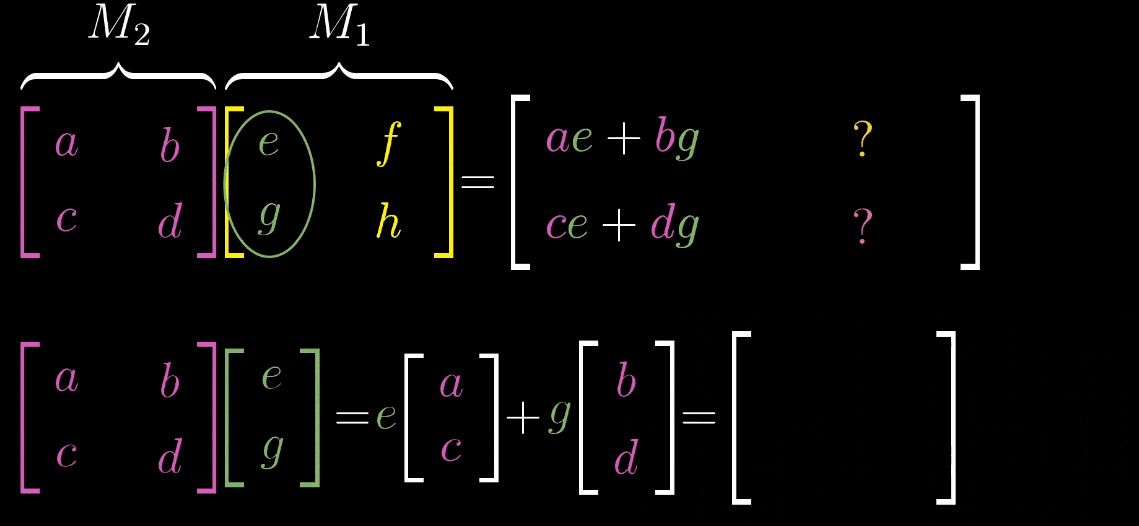
行列式

线性变换将空间拉伸或挤压。

想要测量变换对空间有多少拉伸或挤压，可以测量一个给定区域面积增大/减小的比例。

因为网格线保持平行且等距分布，只需知道单位正方形变化的比例，就可知其它任意区域面积变换的比例。

变换的行列式也就是线性变换改变面积的比例。

正负表达的是方向，j起始状态在i的左侧，如果经过变换，变为j在i的右侧，就添加负号。

只要检验一个矩阵行列式是否为0，就能了解矩阵代表的变换是否将空间压缩到更小维度上。

行列式计算：

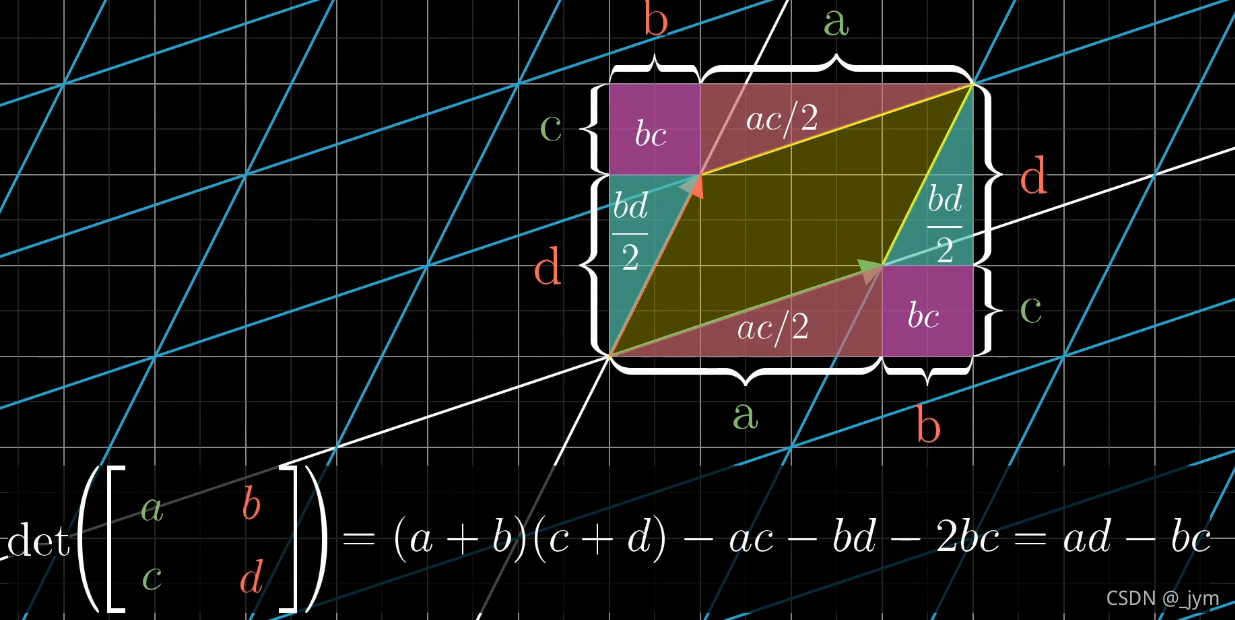
矩阵的用途

描述对空间的操作。

解线性方程组。

线性方程组

一般形式：
$$\mathbf{A}\vec{\mathbf{x}}=\vec{\mathbf{v}}$$

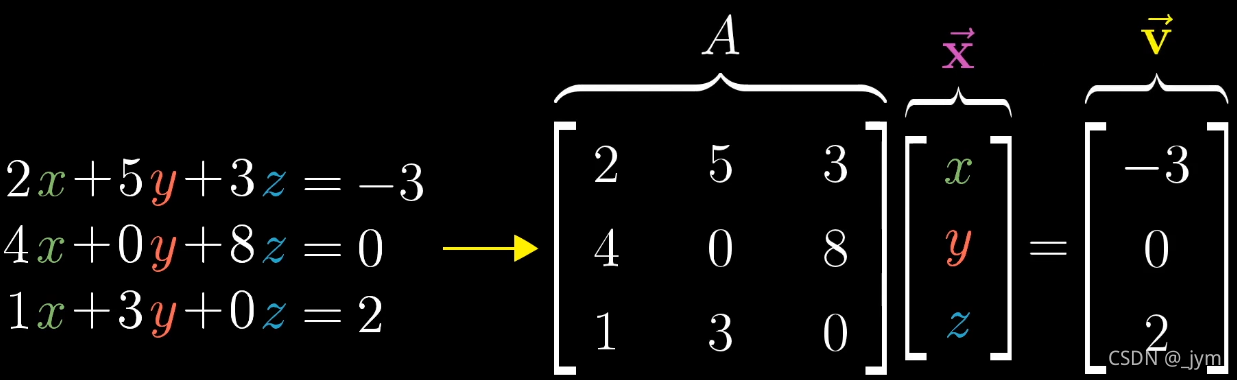
如果这个方程组成立，也就意味着，x经过A矩阵变换后，落在v上。

如果说矩阵行列式为0，也就是说，空间降维了。

举个例子，二维矩阵，行列式为0，那么x经过这个矩阵变换，降维了成了一条直线，这个直线和v共线的话，线性方程组才有可能有解。

逆矩阵

已经变换过的i和j通过逆矩阵变换，能够变回原来的i和j。

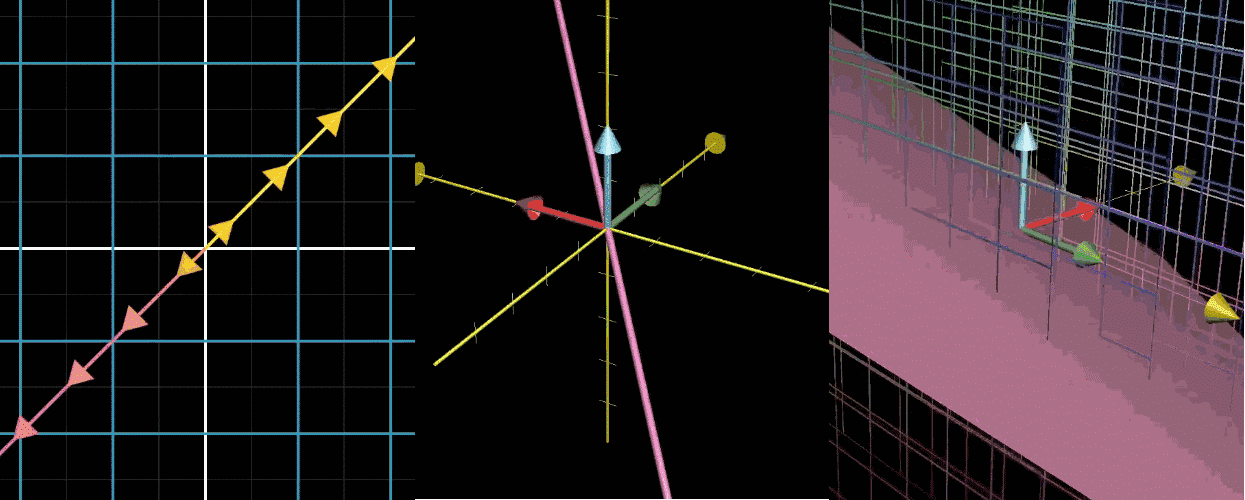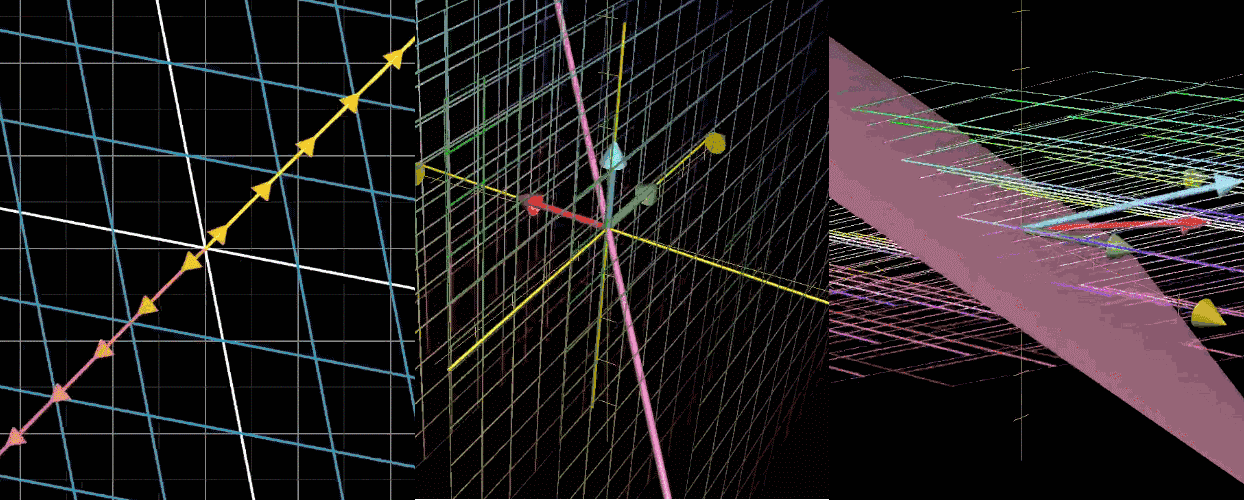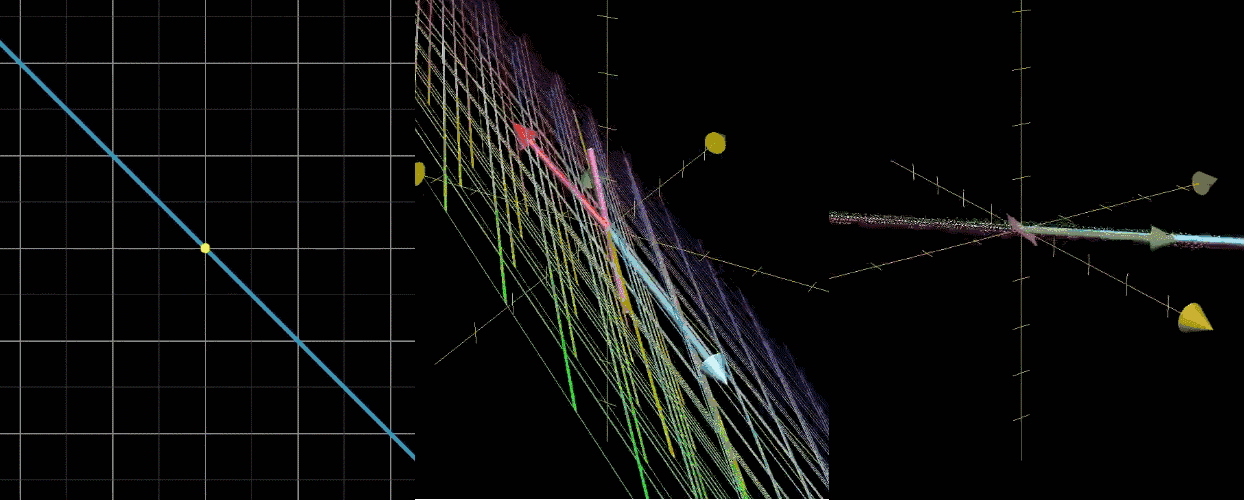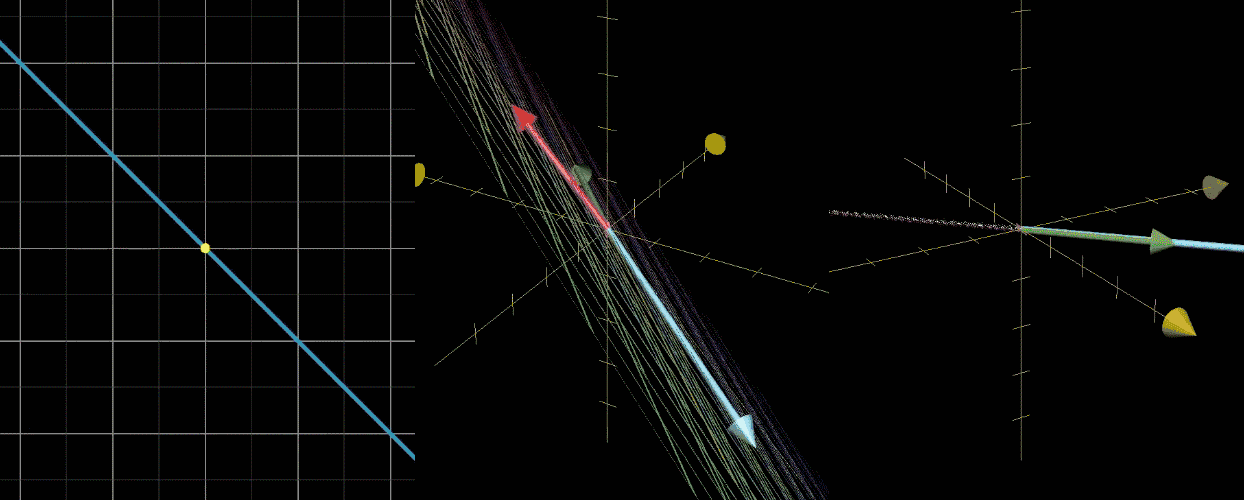
逆矩阵乘原矩阵等于恒等变换。
$$\mathbf{A}{\mathbf{A}}^{-1}=\mathbf{I}$$

列空间

矩阵的列：基向量变换后的位置。

变换后，基向量张成的空间，就是所有可能的变换结果。

列空间：矩阵的列 张成的空间。

举个例子：下图列空间是个一维的。

零空间

经过一个变换，空间被压缩到低维，就导致一系列向量变换后成为零向量。

举个例子，看下图第一个二维降到一维的，和这个直线不同方向上所有向量被压缩到原点。

变换后落在原点的向量的集合叫做矩阵的零空间。

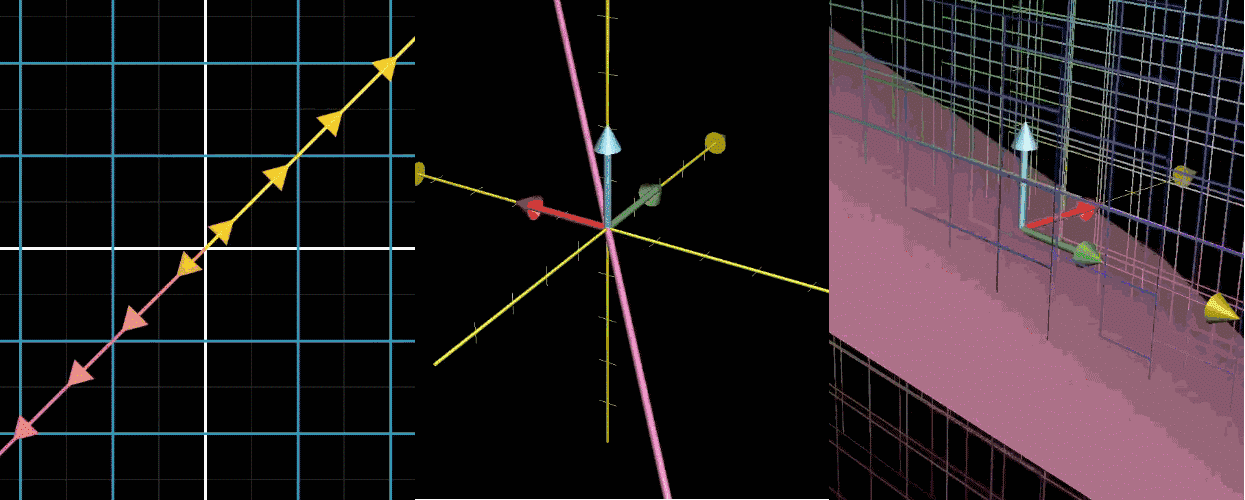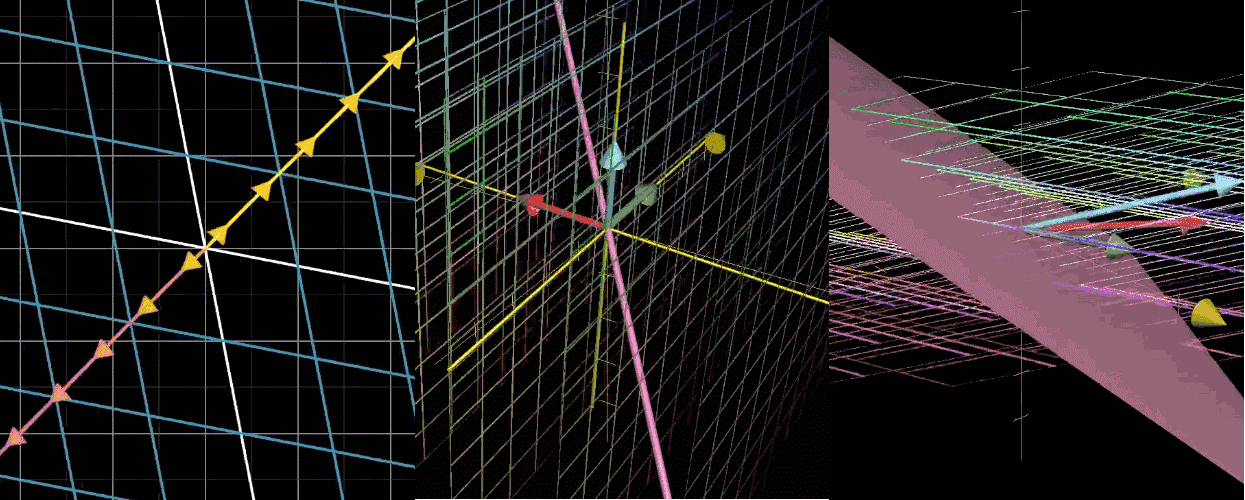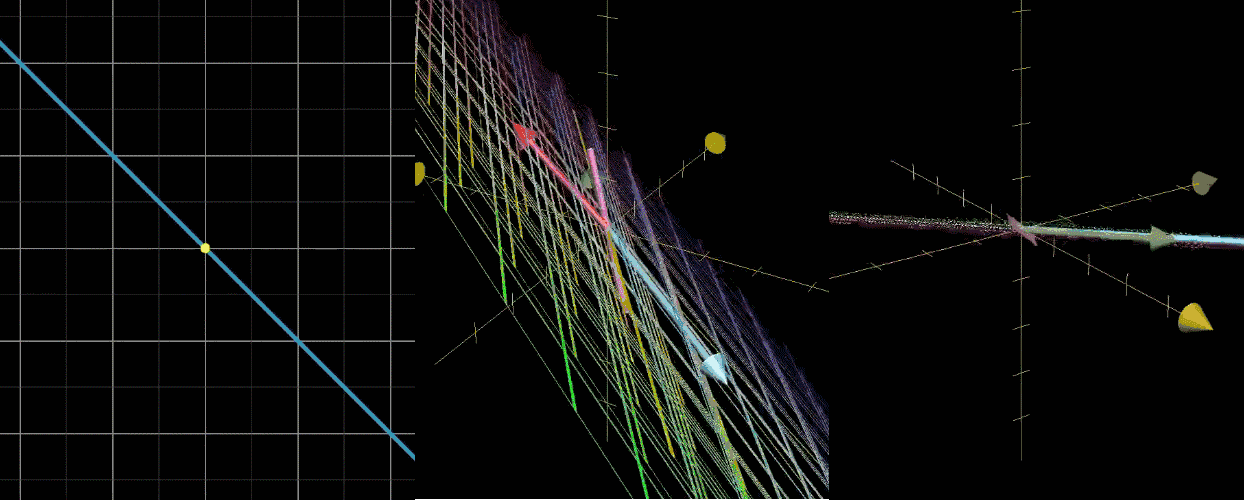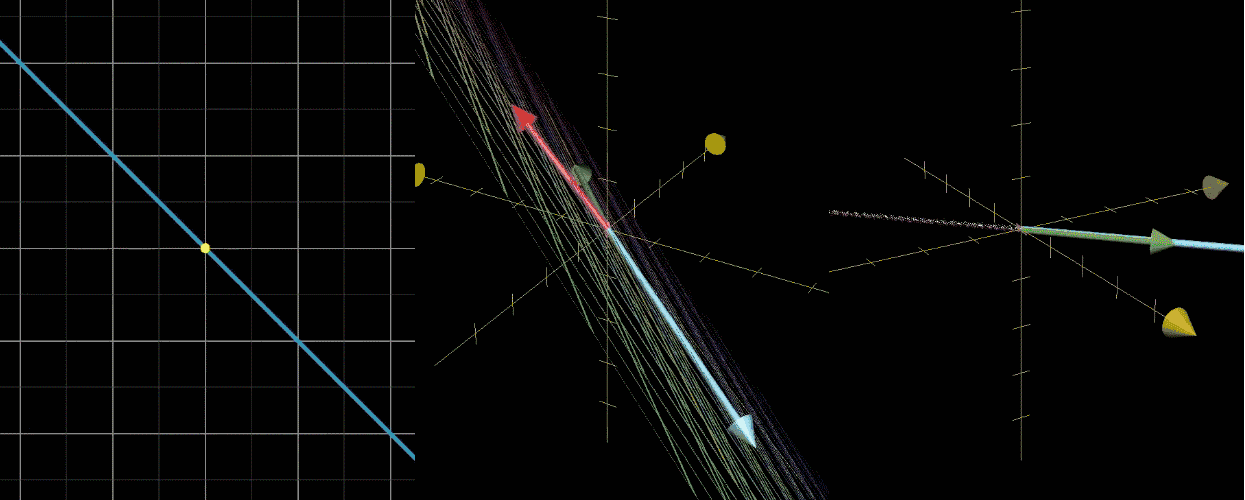
秩

秩：变换后空间的维度，也就是矩阵的列 张成的空间的维度。

举个例子：

矩阵秩为1，经过这一矩阵的变换后，向量落在一条直线上。

秩为2，变换后，向量落在二维平面上。

非方阵

举个例子：
$$\left[\begin{array}{cc}2& 0\\ -1& 1\\ -2& 1\end{array}\right]$$
上面这个矩阵，列空间是三维空间中过原点的二维平面。

两列意味着输入空间有两个基向量，三行说明每个基向量变换后用三个独立的坐标描述。

通过这个矩阵，能做到输入二维向量，输出三维向量。

基变换

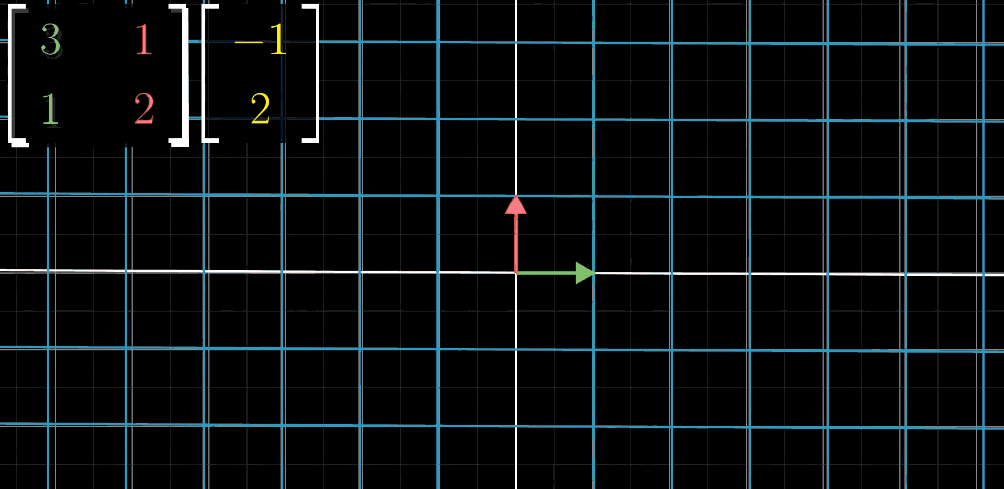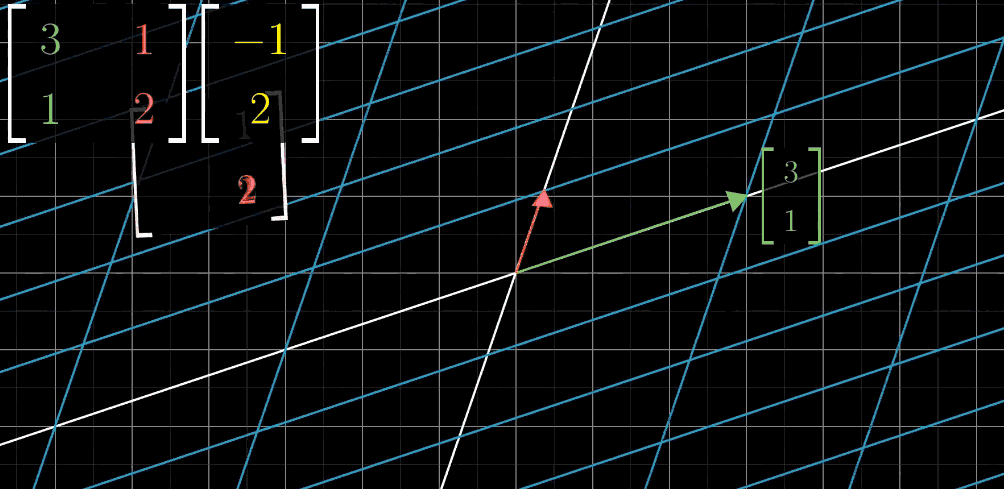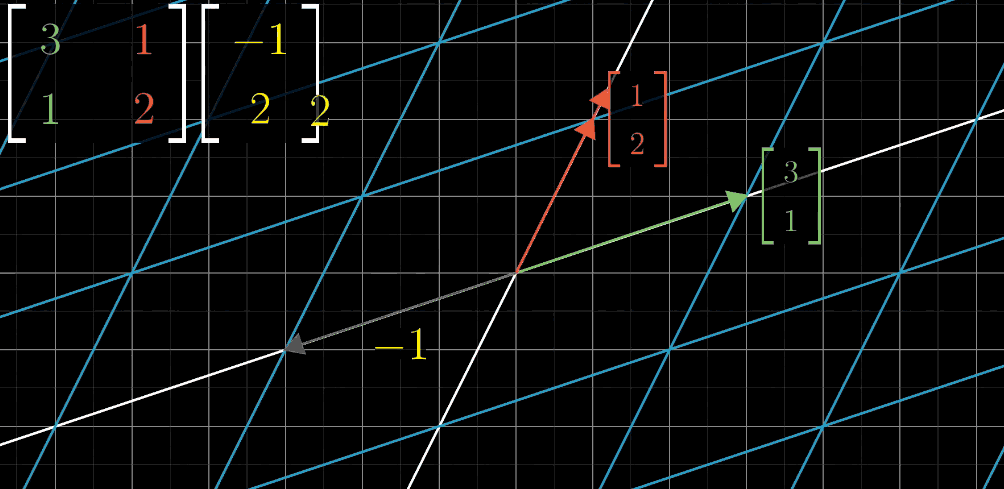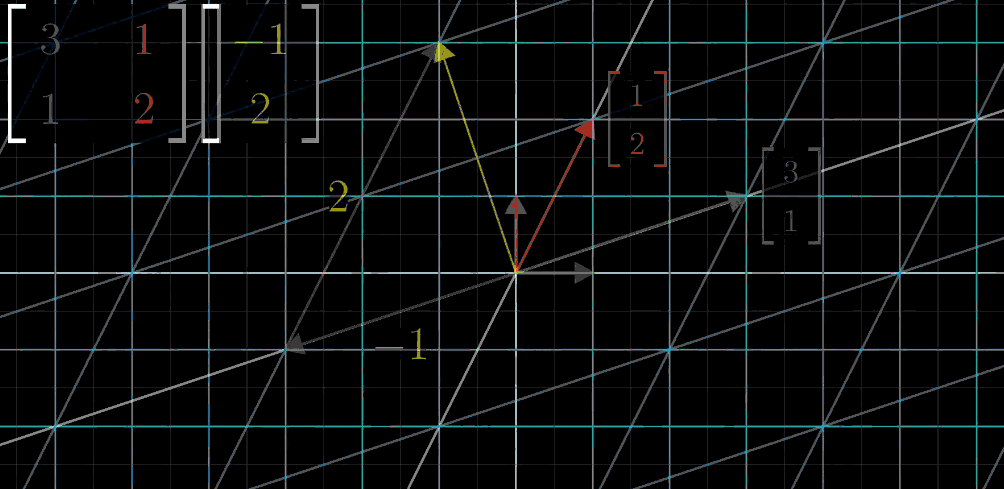
我们一般用的基向量是相互垂直长度为1 的i和j，分别指向上方和右方

如果说使用不同的基向量。

举个例子：

火星人使用的基向量为b1和b2，分别指向右上方和左上方。

黄箭头向量，用我们地球人使用的基向量表示如下：

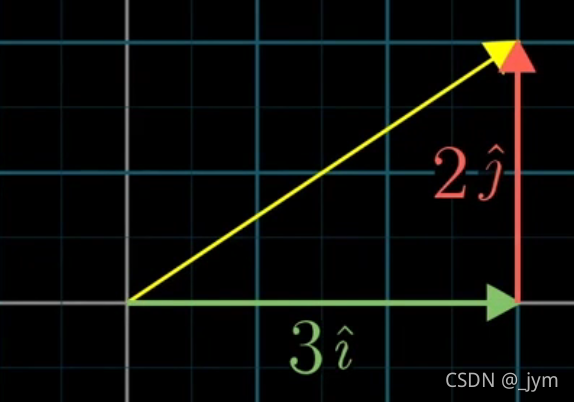
但是，用火星人使用的基向量表示如下：

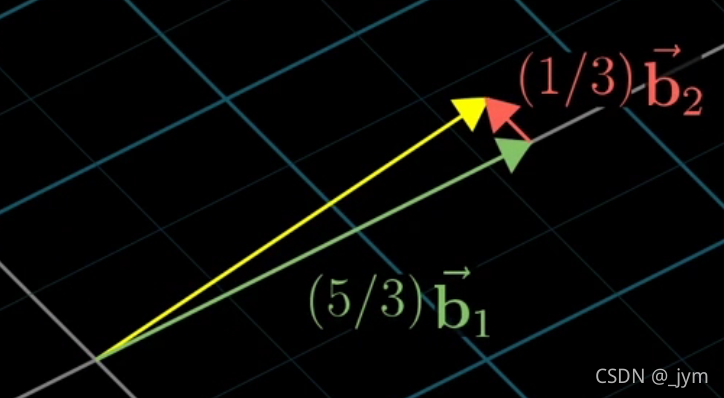
注意，这个黄箭头在空间里面没动，由于基向量不同，这个黄箭头的表示也不同。

也就是说，向量[-1 2]，在火星人眼里，是这样的：

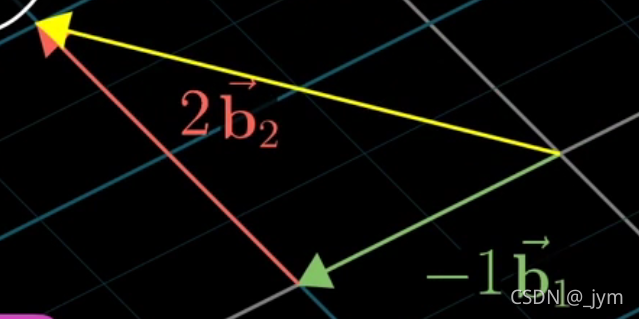
向量[-1 2]，在地球人眼里，是这样：

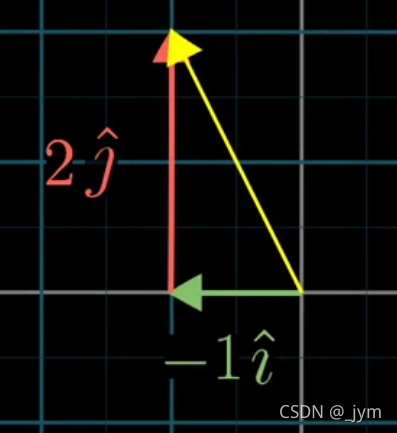
也就是说，同样的描述，未必就是一个东西。

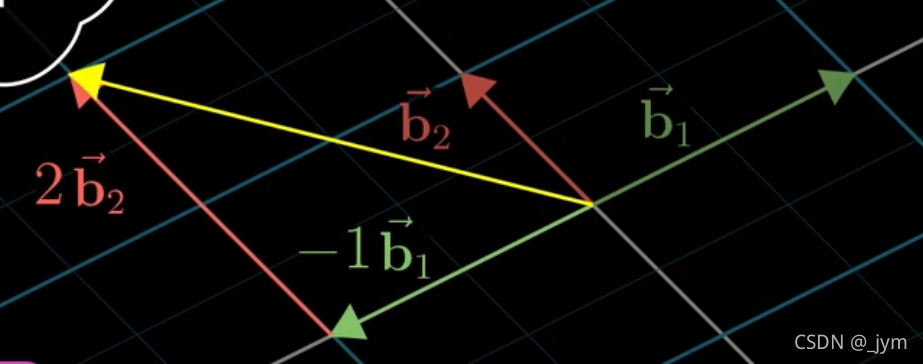
在地球人的眼中，火星人的基向量：

但是在火星人的坐标系中，他们的基向量：

空间中同一个向量可以用不同语言描述。

火星人和地球人坐标原点重合。坐标轴的方向和网格间距和地球人有所不同，这依赖于火星人对基的选择。

如何在不同坐标系之间进行转化？

举个例子：

火星人用[-1 2]表示一个向量，那么这个向量在地球人的坐标系中该如何描述。

地球人的坐标系中，b2=[-1 1] b1=[2 1]

在地球人的坐标系中可以这么表示这个向量：
$$-1\left[\begin{array}{c}2\\ 1\end{array}\right]+2\left[\begin{array}{c}-1\\ 1\end{array}\right]=\left[\begin{array}{c}-4\\ 1\end{array}\right]$$
也就是说:
$$\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]\left[\begin{array}{c}1\\ 2\end{array}\right]=\left[\begin{array}{c}-4\\ 1\end{array}\right]$$
矩阵的列，就是，用地球人的语言表达火星人的基向量。

最后实现了把火星人认为的[-1 2]这个向量，转换成我们认为的[-4 1]这个向量。这个向量在空间中是没有变动的，只不过我们在不同的参考系下，看到的这个向量是不同的。

基变换矩阵

$$\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]$$

以火星人的基向量作为列的基变换矩阵。这个基向量是用地球人的坐标描述的。

通过这个矩阵，可以将火星人语言描述的[-1 2]，转换成地球人的语言描述，也就是[-4 1]。

现在反过来：

地球人坐标系中一个向量是[3 2]，那么这个向量在火星人坐标系中是如何表示的？

通过求基变换矩阵的逆:
$${\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]}^{-1}=\left[\begin{array}{cc}1/3& 1/3\\ -1/3& 2/3\end{array}\right]$$
用这个基变换矩阵的逆乘以[3 2]，就可以知道用火星人语言描述的相同向量。
$$\left[\begin{array}{cc}1/3& 1/3\\ -1/3& 2/3\end{array}\right]\left[\begin{array}{c}3\\ 2\end{array}\right]=\left[\begin{array}{c}5/3\\ 1/3\end{array}\right]$$
以上就是在坐标系之间对单个向量的描述进行相互转化。

对于一个线性变换，比如逆时针旋转90度，用矩阵代表它的时候，是在跟踪i和j的去向。

i变换后的坐标是[0 1],j变换后的坐标是[-1 0]，这些坐标成为矩阵的列。
$$\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$$
这种表示与我们对基向量的选择相关。跟踪我们所选的i和j，并且在我们自己的坐标系中记录他们的去向。

那么火星人该如何描述空间90度旋转。

火星人想要的矩阵，需要代表它的基向量的去向。

火星人语言描述的向量：
$$\left[\begin{array}{c}-1\\ 2\end{array}\right]$$
用基变换矩阵转换成我们的语言，用地球人的语言去描述这个向量：

矩阵的列指的是，用我们的语言描述火星人的基向量。
$$\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]\left[\begin{array}{c}-1\\ 2\end{array}\right]$$
左乘线性变换矩阵：

给出的是，用我们的语言描述的线性变换后的向量。
$$\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]\left[\begin{array}{c}-1\\ 2\end{array}\right]$$
左乘基变换矩阵的逆：

得到用火星人语言描述的变换后的向量。
$${\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]}^{-1}\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]\left[\begin{array}{c}-1\\ 2\end{array}\right]$$
也就是说，三个矩阵复合，给出火星人语言描述的线性变换矩阵。

这个矩阵接收火星人语言描述的向量，输出火星人语言描述的变换后的向量。
$${\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]}^{-1}\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]\vec{\mathbf{v}}$$
v乘以这个矩阵，结果就是在火星人的坐标系中让v旋转90度。

下面这个表达式，暗示一种数学上的转移作用。中间的矩阵M代表我们所见到的变换，外侧两个矩阵代表转移作用，视角上的变化。
$$A^{-1}MA$$
三个矩阵乘积，也就是，从他人角度看的同一个变换。

特征向量 特征值

对于一个线性变换：
$$\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$$
让它作用于一个向量。

大部分向量在变换中都离开了它原来张成的空间。以下图左侧为例，离开了它原来所在的那条直线。

但是还有一些特殊向量，仍然留在他们张成的空间里，如下图右侧。

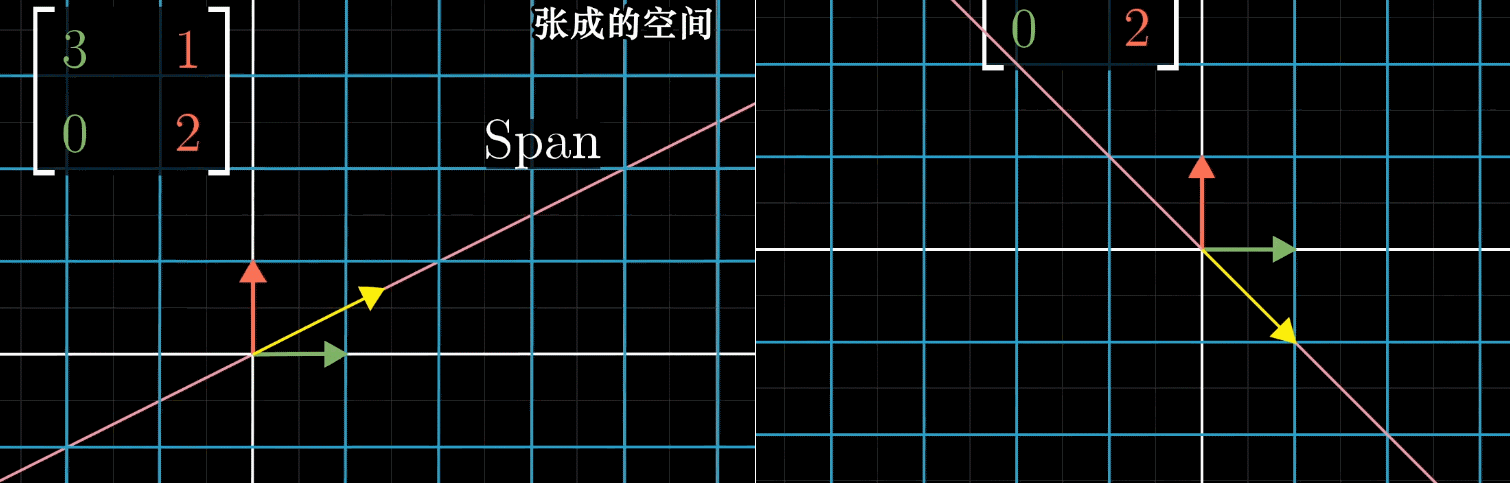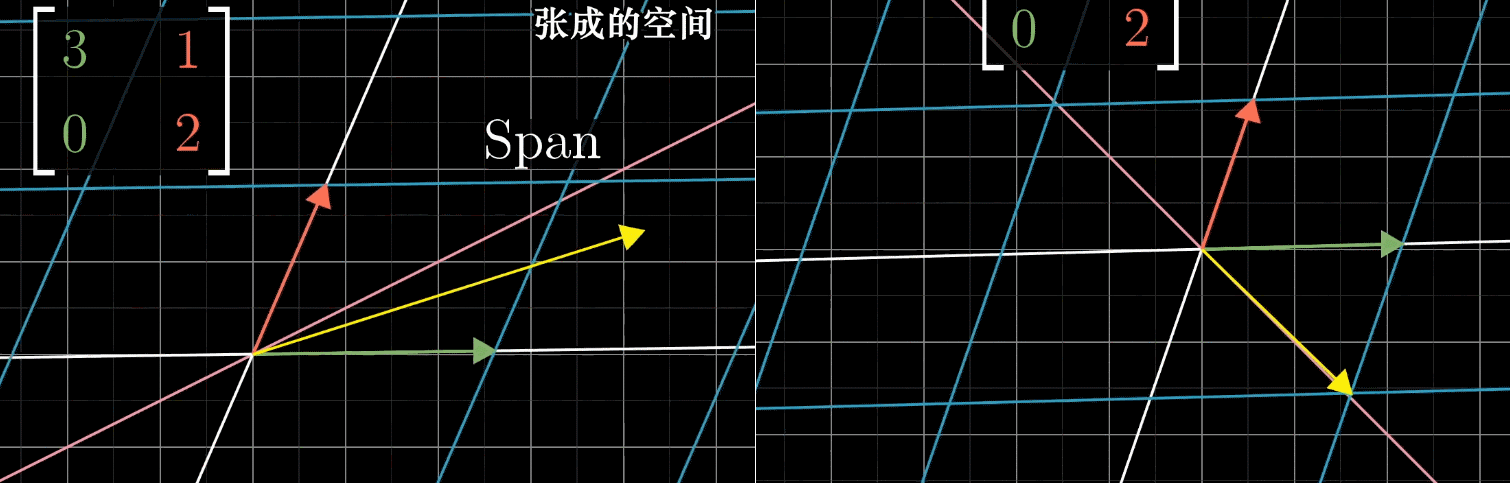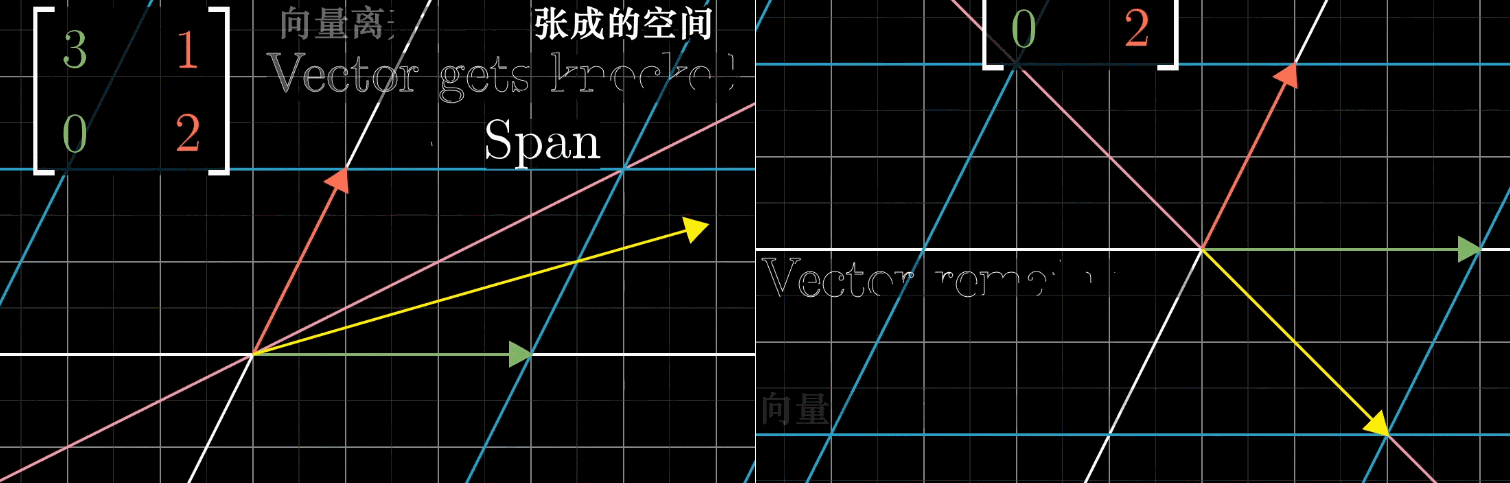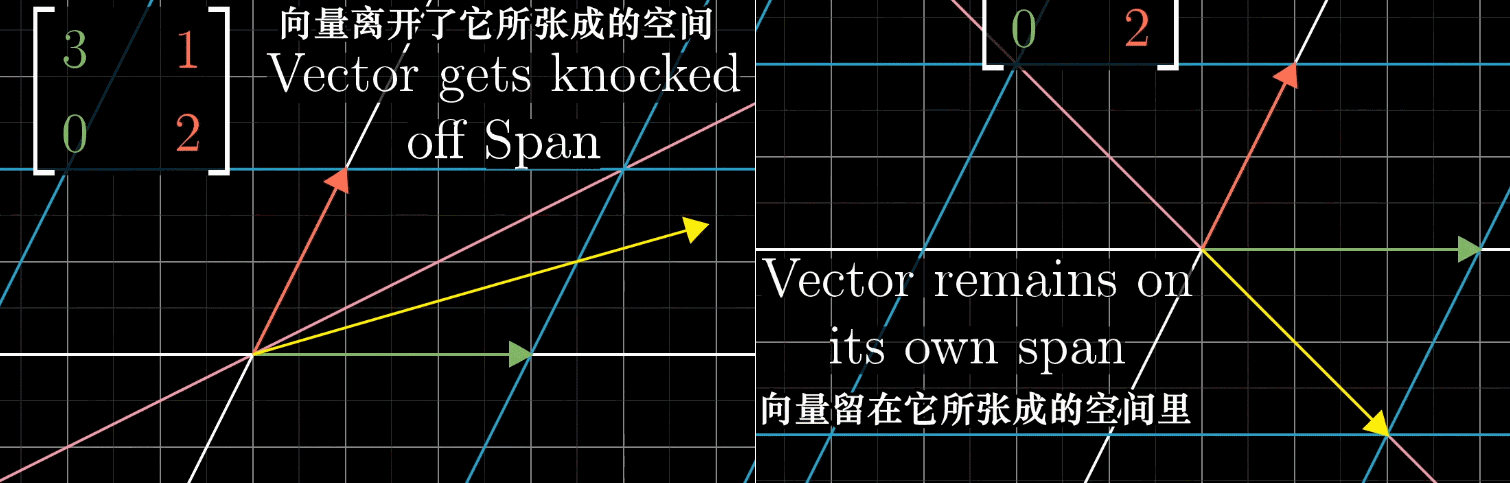
一个向量经过矩阵的变换，仍然留在他们张成的空间，意味着矩阵对它的作用仅仅是拉伸或压缩，它就像一个标量。

对于上面那个线性变换，基向量i就是这样一个特殊的向量，i张成的空间是x轴，经过变换，i变成了三倍，仍然留在x轴。

而且x轴上任何其它向量也是被拉伸为原来3倍。

向量[-1 1]在变换后也留在自己张成的空间，最终被拉伸为原来的2倍。处在[-1 1]所在直线上其他任何一个向量也是被拉伸为原来的2倍。

对上述线性变换而言，以上就是经过这一线性变换，仍然留在他们张成空间里的向量。一个是x轴上的向量，另一个是[-1 1]所在对角线上的向量。

这些特殊向量就被称为变换的特征向量。

特征值：特征向量在变换中拉伸或压缩的比例。

特征值为负数：经过矩阵的线性变换，这个特征值对应的特征向量被反向。

如果说把矩阵的列看做变换后的基向量，他们这个矩阵就是个基变换矩阵。

可以由下图发现，经过基变换矩阵，特征向量仍然在它原来张成的空间里，位置没发生变动。

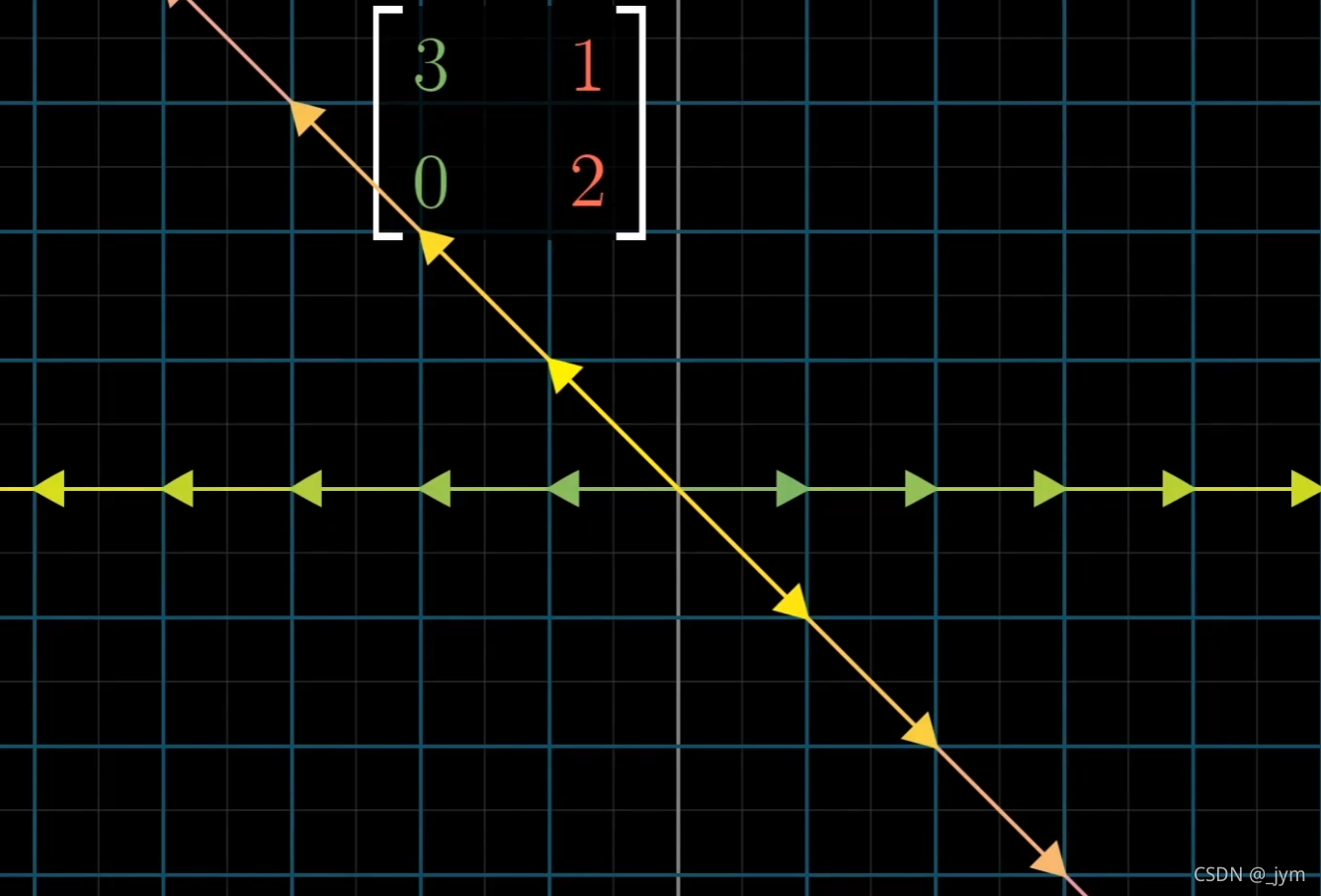
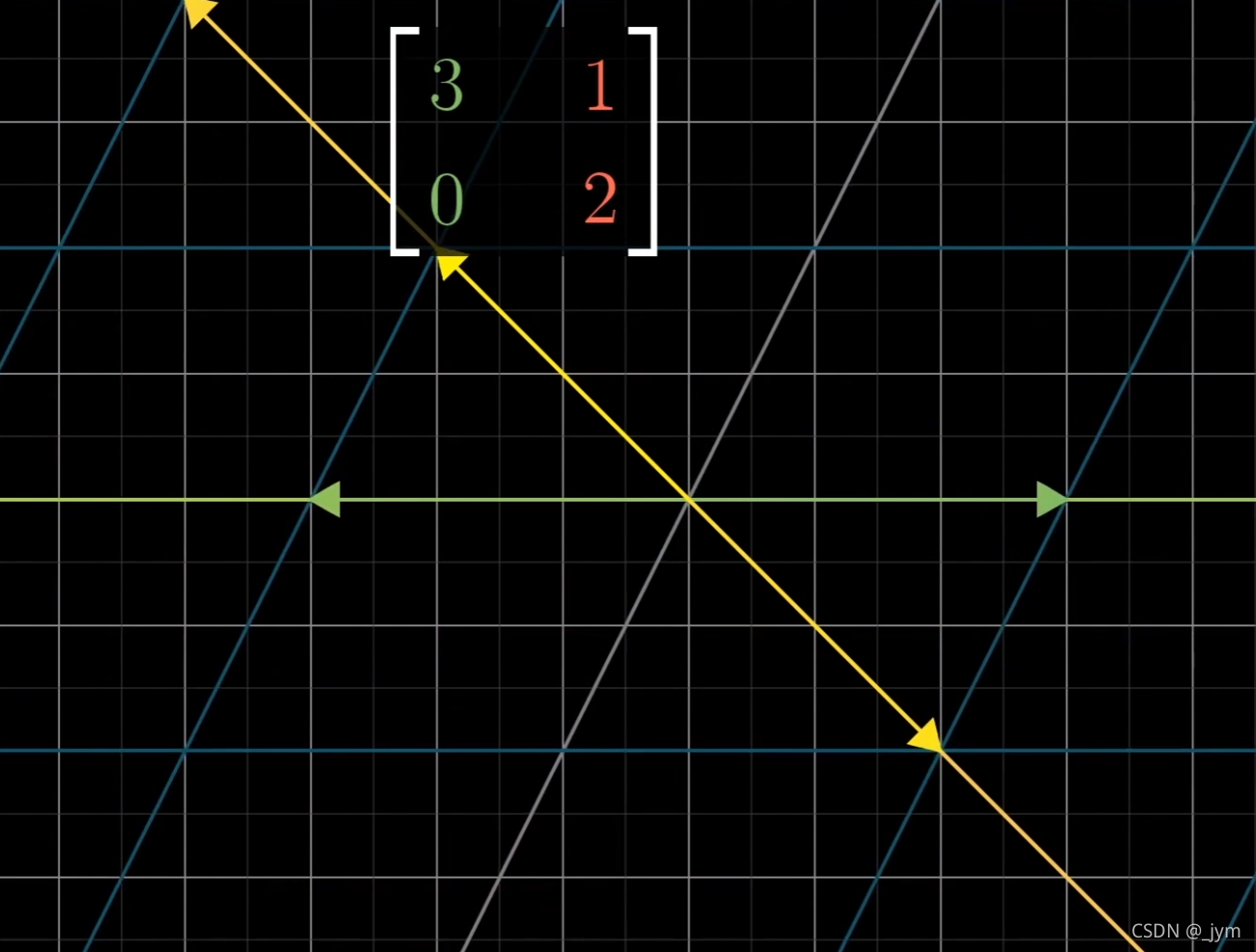
用符号表示特征值和特征向量：
$$\mathbf{A}\vec{\mathbf{v}}=\lambda \vec{\mathbf{v}}$$
A代表某个变换的矩阵，v是特征向量，λ是特征向量的特征值。
$$\mathbf{A}\vec{\mathbf{v}}-(\lambda I)\vec{\mathbf{v}}=\vec{0}$$
转换成：v与新矩阵相乘结果为零向量。
$$(\mathbf{A}-\lambda I)\vec{\mathbf{v}}=\vec{0}$$
当这个新矩阵代表的变换将空间压缩到低维度，才存在非零向量v，使矩阵和它的乘积为0向量。

如上图，向量经过变换后，压缩到原点成为零向量。

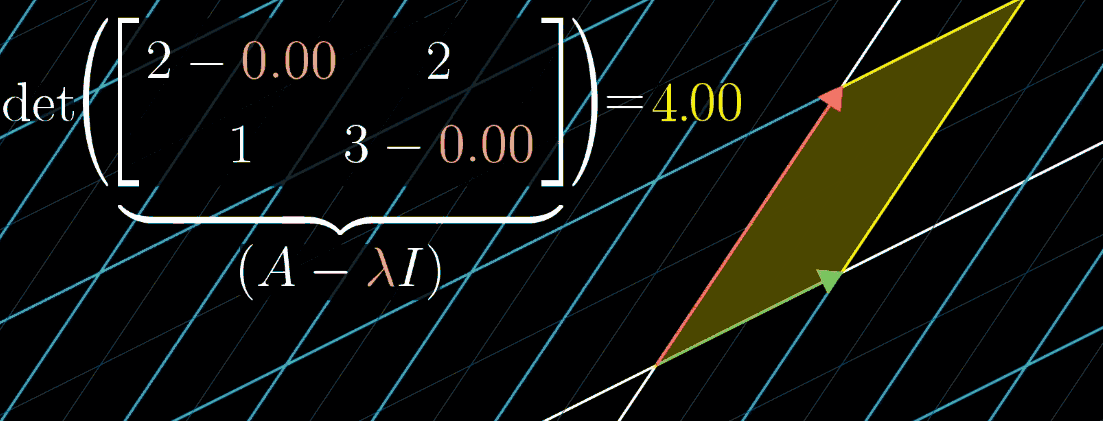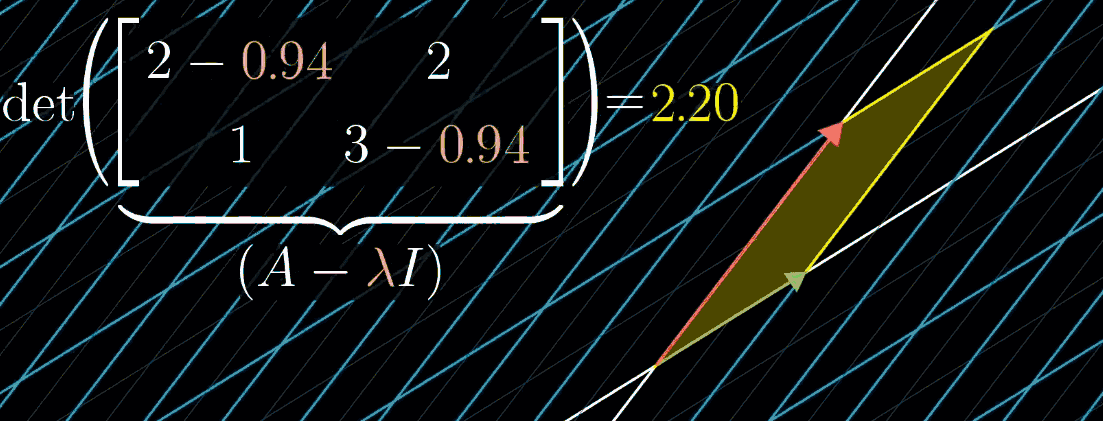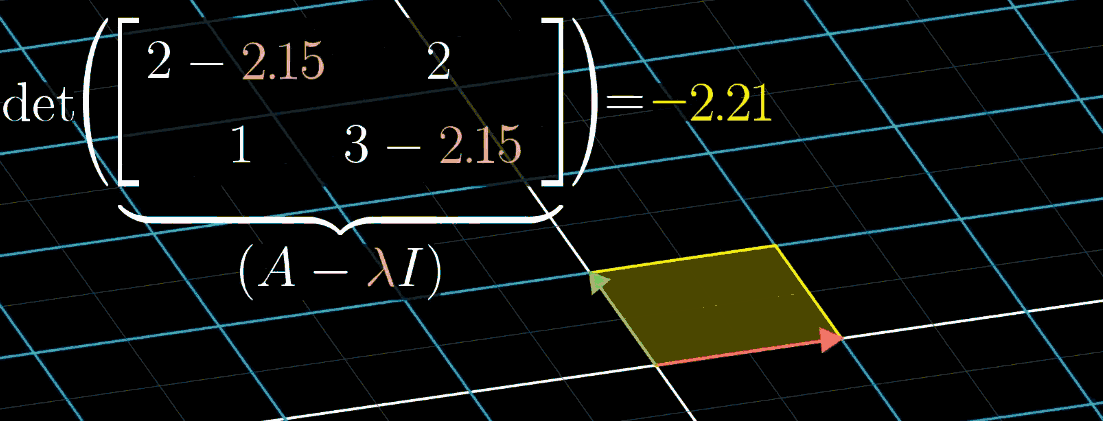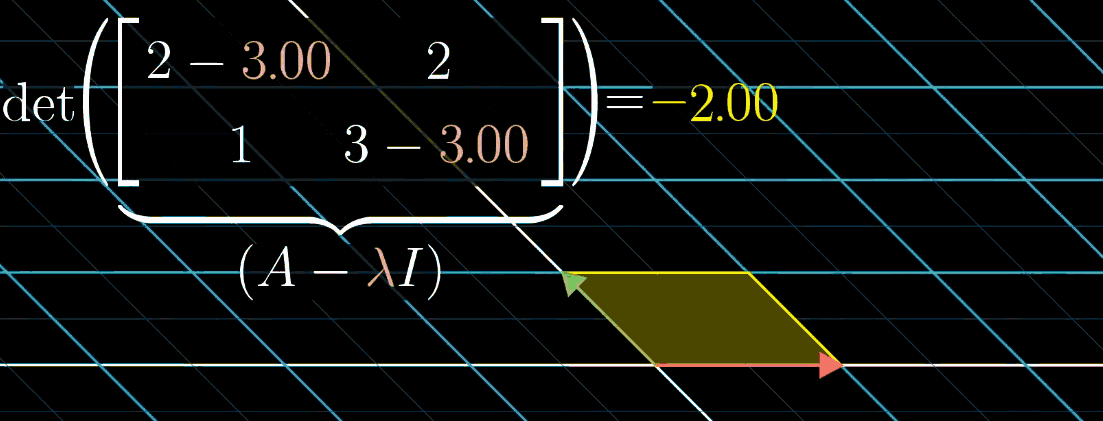
可以找使矩阵的行列式为0的λ。矩阵行列式为0，表示变换将空间压缩到低维度。

上图，λ=1时，这个矩阵将空间压缩到一条直线上，也就是说存在非零向量v通过这个矩阵变成零向量。
$$(\mathbf{A}-\lambda I)\vec{\mathbf{v}}=\vec{0}$$

对于矩阵：
$$\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$$
为了求特征值λ，将对角元减去λ，当矩阵的行列式为零时，λ才会是特征值，然后推断出可能的λ。
$$det(\left[\begin{array}{cc}3-\lambda & 1\\ 0& 2-\lambda \end{array}\right])=(3-\lambda )(2-\lambda )=0$$
将λ的值带入矩阵中，然后求解出经过这个矩阵变换后，成为0的向量。
$$\left[\begin{array}{cc}3-2& 1\\ 0& 2-2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$
然后可以发现，所有解全部落在向量[-1 1]张成的对角线上。

特征向量是不唯一的，只有特征值唯一。

然后原始矩阵：
$$\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$$
将特征向量拉伸为原来2倍。

二维线性变换不一定有特征向量，如下矩阵，实现90度旋转的变换。
$$\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$$
它没有特征向量，因为每一个向量都发生旋转、离开它张成的空间。计算他的特征值，发现没有实数解。

特征基

如果基向量是特征向量。

比如矩阵：
$$\left[\begin{array}{cc}-1& 0\\ 0& 2\end{array}\right]$$
它的特征向量是i、j的话，i的特征值就是-1，j的特征值就是2。

对角矩阵：除了对角元以外，其他元素均为0的矩阵。

所有基向量都是特征向量，矩阵的对角元是他们所属的特征值，

对角矩阵，多次与自己相乘，结果更易计算。

如果变换有许多特征向量，多到能张成全空间。

那就可以变换坐标系，使这些特征向量就是基向量。

在另一个坐标系中表达当前坐标系描述的变换：

首先通过基变换矩阵，用我们的语言描述另一个坐标系中的基向量，然后左乘线性变换矩阵，用我们的语言描述线性变换，然后再左乘基变换矩阵的逆，得到用另一个坐标系语言描述的线性变换。最终得到的变换是从新基向量所构成的坐标系角度看的。

这个新矩阵是对角的，并且对角元为对应的特征值。因为它所处坐标系的基向量在变换中只进行了缩放。

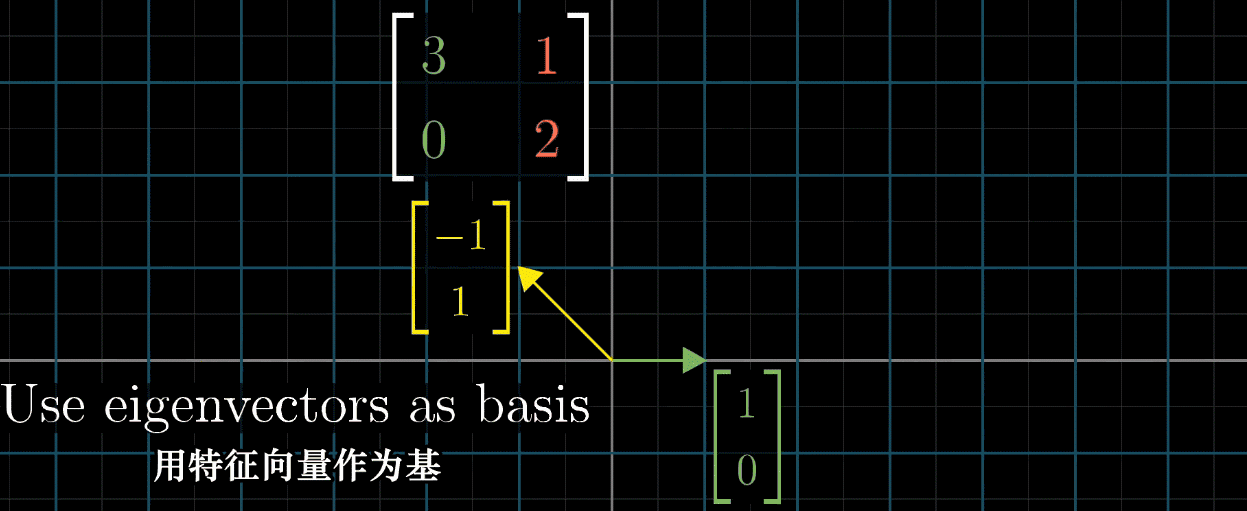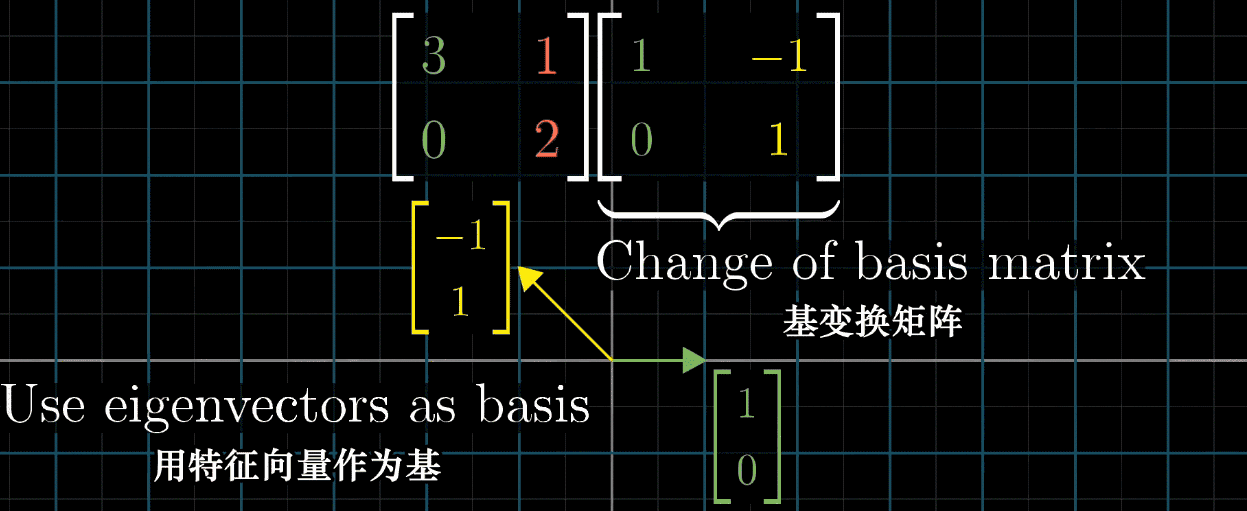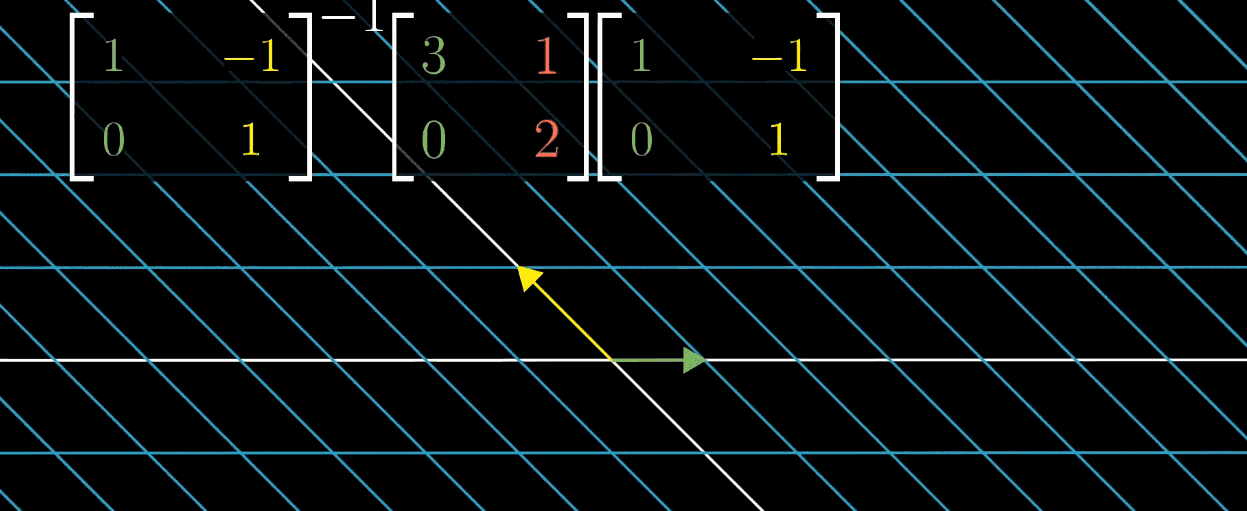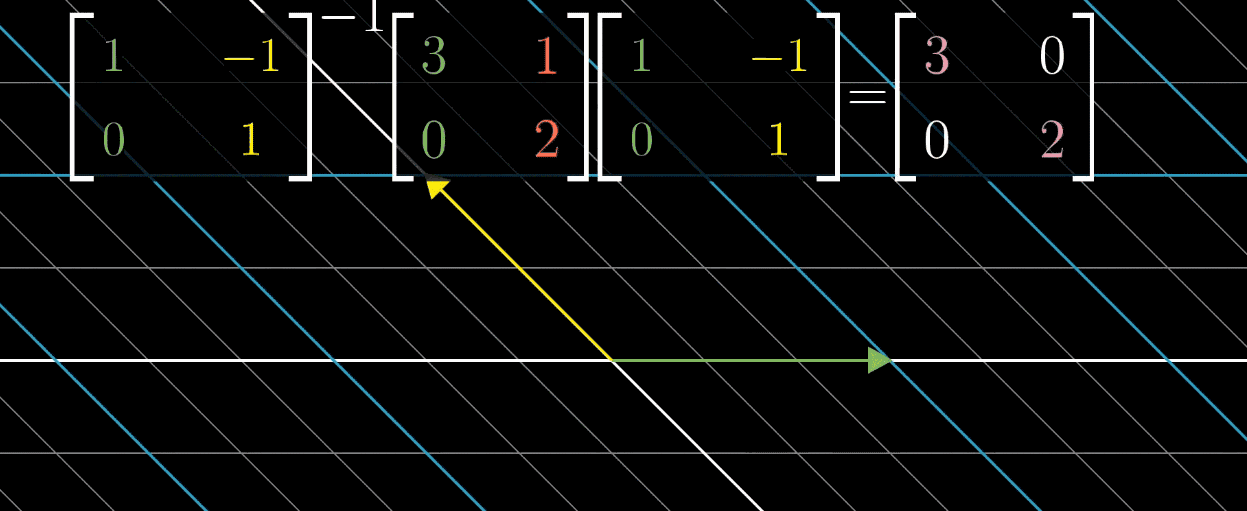
计算：
$${\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]}^{100}$$
可以先变换到特征基，在那个坐标系计算一百次幂，然后转换回标准坐标系。

不是所有矩阵都能对角化，就比如：
$$\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]$$
它的特征向量全在x轴上，不能张成全空间。

关于坐标

我们所处的空间独立于坐标存在。

坐标描述，依赖于所选的基向量。

行列式和特征向量与所选坐标系无关。

行列式，变换对面积的缩放比例。

特征向量，在变换中留在它所张成空间中的向量。

这两者暗含于空间中。自由选取坐标系也不会改变他们最根本的值。

一个线性变换可以通过它对基向量的作用来描述。

求一个向量变换后的结果，实际上就是求出：变换后的基向量，以相同方式进行线性组合的结果。

参考：3Blue1Brown 线性代数的本质