在上一篇文章中,我们介绍了一种最简单的MDP——s与a都是有限的MDP的求解方法。其中,我们用到了动态规划的思想,并且推出了“策略迭代”、“值迭代”这样的方法。今天,我们要来讲更加一般的最优控制问题——t、a与s都是连续的问题。我们仍然假定我们已经清清楚楚知道环境与目标。我们将介绍求解的方法,并引出Hamilton-Jacobi-Bellman方程(简称H-J-B方程)。其中,H-J-B方程是一个t连续定义下的方程,它的离散t的版本被称作Bellman方程。这在强化学习中是极其重要的。
最优控制问题
在最优控制中,我们一般用x来代表状态,用u来代表“控制”,即可以人为输入的东西,和MDP中的动作a是同一个概念。另外,在最优控制中,我们一般不是尝试“极大化奖励”,而是尝试“极小化损失”,也就是说,我们的目标往往是用一个求极小化的形式表现出来(只要加上一个负号就可以实现二者的转化)。除此之外,最优控制与MDP最大的不同在于其t是连续的。在进行了概念的对应之后,最优控制的逻辑和MDP都是一样的。
按理说,s与a是连续的时候,也可以将动作、状态的转移建立为一个概率方程。例如给出在
一般的最优控制问题有如下几部分组成(用x记状态、用u记控制/动作)。首先是给定初始与终止的时间
如果问题是time-invariant的,则可以去掉t变量,即变成
问题的目标是极小化损失函数:
同理,对于time-invariant的问题,f中的t变量可以省略。作为目标的损失函数分成两个部分,一个是在路径上累积损失,用f记录,另一个是最终状态对应的损失,用H记录。路径上的累积损失意思是在时间微元
很多问题可以转化为最优控制问题。例如对于一个在平地上开汽车的问题,限定一定时间内(截止为

有了最优控制问题之后,我们当然可以开始对其进行求解。这里的t、a与s都是连续的,而对于状态转移方程函数
作为最优控制的例子,我们可以先考虑一种最简单的、可以求出解析解的最优控制问题。那么,怎么才算是“最简单”呢?
首先,我们希望Dynamic
然后考虑损失函数
这种Dynamic是线性(Linear),而损失函数是二次函数(Quadratic)的情况是最简单的一类最优控制问题,我们将其称作LQR(Linear-Quadratic Regulator)。一个time-invariant的,并且没有状态与控制的交错项的LQR,就是我们所找寻的“最简单的”问题:

上述的LQR是最优控制中最简单,同时也是最经典的一类问题,常常被作为最优控制教材的“入门问题”出现。对于这类问题,我们可以不对x与u进行离散化,而直接精确地求出其最优解的表达式。
针对不同的最优控制问题,或简单,或复杂,我们同样利用动态规划的思想,可以有几种不同的解法。其中最主要的问题是,我们是否要对连续的t进行离散化。如果对t进行离散化之后,对于简单的LQR问题,我们有比较简单的方法求出解析解(不用对x与u离散化)。而对于非线性的系统,我们则只能对x与u进一步离散化,求近似的数值解;如果我们选择不对t进行离散化,则可以将问题转化为一个偏微分方程,也就是我们今天的主题Bellman方程。(有许多非线性pde求不出解析解,同样只能求数值解,但这又是另一个问题了)。这几种情况中,核心的思想都是动态规划。
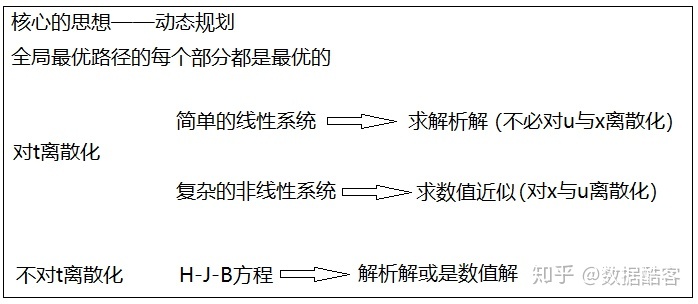
下面,我们就来一一介绍这些方法。
离散化t求数值解
面对t连续的问题,尤其是非线性的、复杂的问题,我们无法求出精确的解析解。所以,将t离散化不失为一种明智之举。
将t离散化之后,关于t的连续函数

我们首先来讲LQR问题的求解方法。这个过程中要利用到我们上一章动态规划的思想,以及对于“价值”的定义。我们不妨设t是从0到100的:
首先,我们已知在最终状态下,状态
然后,我们考虑t=99的时候,已知状态
接着,我们考虑t=98的时候,
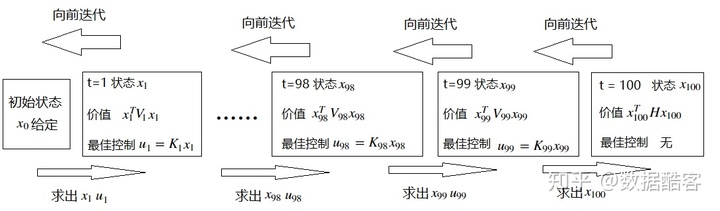
接下来,我们可以不断地重复这个过程。由于LQR的定义——Dynamic是线性,而惩罚函数是二次的这个性质,最佳控制
我们一直重复这个迭代过程,直到初始状态
对于非线性的问题,我们也想要仿照上述的方法。但是,如果将过程中每一步的最佳控制与价值表达为状态的解析表达式,可能会得到极其复杂的表达式。例如,如果将LQR中的Dynamic从线性的形式改为二次的形式,则我们会发现迭代了几步之后就无法再迭代下去了。对于这样的情况,我们无法求解析解,只能考虑通过离散化x与u来求数值解。
例如,我们将x、u离散化为10段得到一个状态有共10种,控制有
首先,考虑所有最终状态对应的价值:
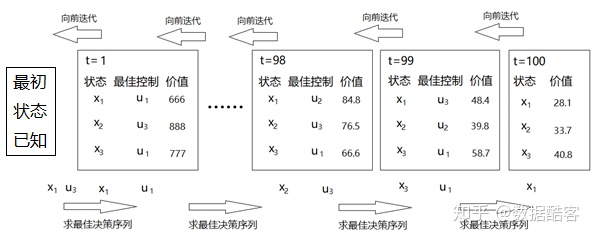
然后,计算t=99的时候从所有状态出发时能够获得的价值。我们应该遍历能够采取的控制u,来计算每个状态的价值。例如对于状态$x_1$,采取$u_1$控制会让其进入$x_8$的状态,那么它就能在t=99到t=100的瞬间内获得$f(x_1,u_1,t)$的“累积损失”,并且获得$H(x_8)$的“最终状态损失”。我们对状态$x_1$计算每一个$u_i$带来的“累积损失”与“最终损失”之和,挑出其中最小的(注意最优控制问题的目的是要让损失最小)。我们可以得到一个这样的结论:在t=99的时候,对于状态$x_1$,采取$u_3$是最好的,它可以让后面发生的损失低至48.4。此时,我们就将48.4记作$x_1$的“价值”。
接着,计算t=98时候所有状态x的价值,以及其对应的最佳控制u。这个过程要用到上一个步骤的数据,例如t=98时,在$x_1$采取$u_1$,除了会立即获得一个“累积损失”之外,还会在t=99的时候就会进入$x_6$。而t=99的时候$x_6$到底好不好,我们就要参考上一个步骤计算出的各个$x_i$在t=99时候的价值。这个步骤结束后,我们可以得到形如这样的结论:t=98时,对于状态$x_1$,采取$u_2$是最好的。它可以让后面发生的损失低至84.8。然后,我们就将84.8记作$x_1$的“价值”。
接下来,不断向前迭代上述步骤。要注意的是,迭代的每个步骤中必须将所有的中间结果保留下来。例如在t=84的时候$x_1$的价值很大,也就是说t=84时候进入$x_1$后面会面临很大的损失,所以不是一个好的选择。但是你不能因此就将这条数据丢掉,因为说不定你的前半程可以只用很小的损失来到这个状态。我们不断向前迭代算法直到t=1的时刻。当我们算出t=1的时刻,各个状态x对应的最优控制u与价值的时候,我们就可以考虑在t=0的初始状态
对于原本的问题,由于有100个回合,每个回合都有10种控制,所以有
细心的读者可能发现了,我们上面讲到的两种迭代本质上是一样的,都是要向前求出“最佳控制”与“价值”关于当前状态的表达式。在LQR中,由于表达式是线性的,或者是二次的,所以我们可以真真切切地把解析表达式求出来。而在复杂的非线性问题中,由于我们求不出解析式,所以我们只能用离散化的方法,用一张表格的形式记录状态与“最佳控制”以及“价值之间”的对应关系。可以想象,如果将表格记录的内容可视化,我们会看到一个高度非线性、无法求出表达式的函数图像。

上面所说的方法和我们上一章讲的“井字过三关”的思路其实是一样的,都是对状态建立“价值”,然后向前迭代求解。并且,因为我们的模型是确定性的,所以每次计算价值的时候不用计算期望,所以计算过程事实上还要简单很多(在“井字过三关”中,我们由于利用了画图求解的直觉,以及对称性,所以省略了很多步骤。如果将其严谨写出来会很繁琐)。
对于LQR问题来说,我们采用解析式迭代的方法可以求出比较精确的解。但是对于非线性的问题来说,离散化的时候我们会面临计算复杂度与精度的权衡取舍。因为在离散化的时候,我们可以人为地选择将x分成10个不同的状态,也可以分成100个不同的段。如果我们选择将x与u均分为更多的段,这意味着结果的精度更高,但同时也意味着计算的时间复杂度会更多;如果将x与u只分成较少的段,计算的时间复杂度会降低,但是计算的精度却会下降。并且由于算法是迭代的,这种误差传递到后面可能会变得很大。如何权衡取舍这两者得到综合最佳?这并不是一个简单的问题,需要视具体情况而定。
H-J-B方程
在上面一节中,我们首先对t进行了离散化,然后再针对问题简单与复杂的情况,分别介绍了求解析解以及离散化求数值的方法,它们都是通过迭代而实现的。那么,我们现在的问题是,能不能不要对t进行离散化,而是把t作为连续变量来直接求解析解呢?答案是肯定,并且,这正是我们本节主题——H-J-B方程的内容。
事实上,推出H-J-B方程可以说和我们上一节思路是完全一样的,只不过是将时间的差分
定义一个价值函数
在最佳$u(t)$作用下,我们能够获得的总价值为
根据
对
将上面两个式子相减,再除以$dt$,并且让$dt$趋于0,得到以下方程:
这个过程可以类比于上一节中我们从后向前迭代推出V表达式的过程。本质上,V是一个关于x与t的二元函数。上一节中,我们迭代中将V拆分成了
将环境
这个方程就是大名鼎鼎的H-J-B方程。我们将
将
这里贴一个公开课上H-J-B方程的截图。要注意其使用的符号可能与我们有所出入:

下面,我们来看一个求解H-J-B方程的简单的例子:
环境方程为
惩罚函数为
首先,我们有哈密顿量
它关于u的导数为:
解出H关于u的一个驻点为
然后,我们发现
这也就意味着,
我们将
方程:
边界条件:
这就是一个典型的关于二元函数
这便是我们所求的最优控制问题的解析解。
细心的读者可能想到,我们举的这个例子其实也是一个“最简单”的LQR问题。如果这不是一个LQR问题,而是一个更加复杂的非线性问题,我们还能这样求解吗?实话实说,我们只能保证可以按照H-J-B方程的定义将pde列出来,但是却不能保证求出解析解,因为有许多pde是没有办法求解析解。对于这样的pde,唯一的方法仍是求数值解。而一旦我们考虑求数值解,那又要离散化t。这也意味着,求H-J-B方程数值解的过程,事实上和上一节讲的离散化t求迭代算法是完全等价的。所以说,离散与连续之间可以相互转化——离散问题的极限情况有助于我们理解连续的方程是怎么推导出来的,而连续方程有时候又要借助离散化来求近似的数值解。
总的来说,只有在问题比较简单,例如LQR问题的情况下,我们可以离散化t以求迭代的解析式,也可以不离散化t,直接求解H-J-B方程的解析解;而在问题比较复杂的问题中,我们只能求数值解。哪怕是列出了H-J-B方程,还是只能求方程的数值解。
这两期的总结
最优控制中有两大类算法,一类是动态规划与H-J-B方程,另一类是变分法与庞特里亚金原理。在上一章与本章中,我们着重讲了动态规划与H-J-B方程。它有一个基本的思想,即把全局最优的解的每一个部分单独挑出来也是最优解。根据这个原理,就可以将一个整体的问题给拆分成局部的小问题,依次求解,大大地节省计算量(从指数复杂度降低到线性复杂度)。用来连接“大问题”与“小问题”的量就是“价值”V。我们讲到的所有算法都围绕着“价值”的计算和极大化而展开。
在这两章中,我们讲的问题给人一种感觉——只有比较简单的几类的最优控制问题可以解决。第一类是s与a(或者x与u)都是离散的,它们之间具有确定性的转移关系的。我们可以用本文中第二节的迭代方法解决;第二类是s与a都是离散的,它们之间具有随机转移关系的。这类方法和第一类差别并不大,只要加一个期望就行了。由于我们讨论的是完全已知模型的情形,所以期望公式可以直接得到;第三类是s与a是连续的,但是其中的转移关系是比较简单的,比如LQR。其他的问题,例如s与a是连续的,并且转移关系很复杂的情况,是没有办法求解的,只能通过离散化使之成为第一类来求近似的数值解。
在强化学习中,有两种解决问题的思路,一种是基于价值的方法,另一种是基于policy的方法。其中,基于价值的方法正是从最优控制问题中动态规划方法发展而来,它同样也是通过拟合“价值”来求解最佳策略。不过,强化学习还将动态规划的思路结合了深度学习的方法。在最优控制中,我们认为只有s与a之间关系是简单的线性关系时才能求解析式,而当它们关系是复杂的非线性关系时,就只能先离散化s与a,再用一个表格的形式去记录s与a的对应关系。但是,当我们有了神经网络这个工具后,我们就可以尝试去拟合任意复杂的非线性函数,无论是s与a之间或是s与V之间的关系。这也使得我们不必拘泥于上面三种简单的情况,而可以考虑更加复杂的情况。
另一方面,强化学习也有十分困难的地方。例如在这两章中,我们都假定完全已知模型。这才导致s与a之间的转移关系具有随机性的时候不会显著增加问题的难度——因为我们已知转移概率,可以直接列出期望的表达式。但是,当我们未知模型的时候,如何能够准确地近似出V?如何减小估算的偏差与方差?如何避免局部收敛?这就涉及到探索-利用(explore-exploit),同策略-异策略(on-policy)之间的取舍,大大地增加了问题的复杂度。这些我们接下来都会慢慢讲到。















 从傅里叶级数到傅里叶变换...)


:Mybatis初始化1.3 —— 解析sql片段和sql节点)
