在上一部分当中，得到了利用三角函数表示周期函数的方法，但是对于非周期函数就...凉了。所以有什么办法吗？没办法（划掉）。这时候我们就需要拿出来我们的黑科技——傅里叶变换。
一、傅里叶级数的推广
当然这东西肯定不是凭空脑补出来的，而是将傅里叶级数进一步推广到非周期函数上。现在已经得到了周期函数的情况，一种很自然的想法就是将非周期函数化归到周期函数上，那么就可以继续套用傅里叶级数了。
如果要强行描述非周期函数的周期性，那它的周期就应该是无穷大，整个定义域都在它的一个周期内，以至于它不可能再重复这一周期。
把这个想法用形式化的语言表示出来，就是
当
傅里叶级数中
换句话说，对于任意的
这个积分需要积一整个周期，而此时的周期为无穷大，也就是整个定义域上都需要积，所以要从
只需要让上式中的
因为
但是这对无穷大和无穷小的阶并不好比较，我们得不出
现在有了傅里叶级数对应的系数，该搞一搞
因为
同时
至此便推导出了傅里叶变换的两个公式
上式称为傅里叶变换，下式称为傅里叶逆变换。
还有另一个版本的傅里叶变换是
这两个版本都差不多，不过就是
二、傅里叶变换的条件
由于傅里叶变换是从傅里叶级数推导得来的，所以还是狄利克雷条件，不过此时还要加上第三条，
这一个条件在
三、性质
以下均默认
函数的卷积
1、线性性质：
2、尺度变化：
3、对称性：
4、时移性：
5、频移性：
6、时域卷积定理：
7、频域卷积定理：
8、微分运算：
这些运算性质都是在采取第一种形式的傅里叶变换下的性质，如果使用第二种形式，会在某些性质上带来常数因子上的差别。
前面的7种运算性质的证明用积分的性质，再做点变量代换乱搞搞就可以了。这里主要说下微分运算性质的证明，用分部积分。只用证一阶导的情况就可以了，证出来之后使用数学归纳法可以很容易地推广到任意阶导数的情况。
微分运算的性质使得傅里叶变换能够将复杂的微分运算转化为简单的乘法运算，所以这个性质的常见应用在于解微分方程。通过傅里叶变换使微分方程变为代数方程，解出代数方程后再利用傅里叶逆变换求出原微分方程的解。
举个栗子，解物理上的简谐振动方程，除了常用的特征根法，还能够使用傅里叶变换
令
定义
使得
解出
进行逆变换
使用辅助角公式合并
傅里叶变换在微分方程上的应用不局限于此，还能够应用于偏微分方程。但是最常用的并不是傅里叶变换，而是它的一般形式拉普拉斯变换
四、广义傅里叶变换
在实际问题当中，经常会遇到一些函数并不满足绝对可积的条件，因而它们对应的傅里叶变换积分发散，并不存在傅里叶变换。但是我们又需要它们的傅里叶变换，所以就有了广义上的傅里叶变换。
比如刚刚求的简谐振动方程，对应的代数方程解出来后，发现
考虑正余弦函数，它们严格意义上的傅里叶变换都是不存在的，但是可以表示为
五、几何意义
傅里叶变换的几何意义类似傅里叶级数，当
实际上，无论是傅里叶级数还是傅里叶变换，都是在无穷维的希尔伯特空间中，将函数定义为空间中的向量，通过三角函数这样一组基向量表示空间中的任意函数。
六、物理意义
emm这一部分跟数学和oi的关系都不是特别大，就大概简略的写一下了，详细的介绍在网上也有很多资料，详细写的话怕是能再写这么长一篇文章（我懒）。
傅里叶级数将函数分解到离散的频率之上，而傅里叶变换将函数分解到连续的频域中，这样使原本频域上离散的点变成一条连续的曲线，对应的就是
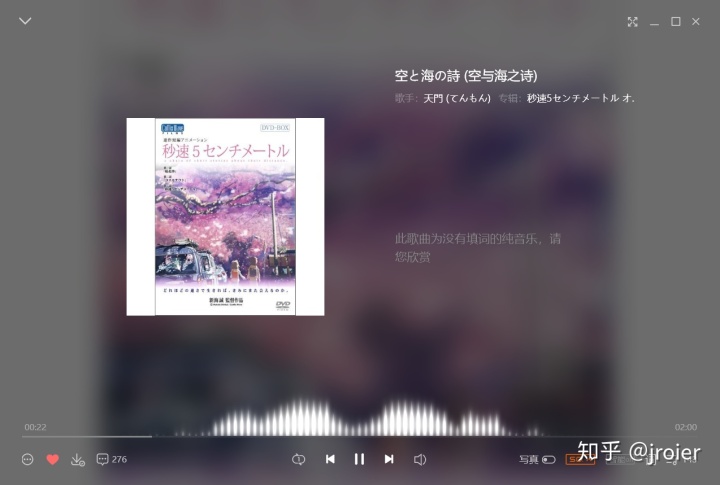
基于这样的物理意义，傅里叶变换在实际问题当中得到大量应用。比如说最常见的是音乐软件上那个疯狂抖动的条，我也不知道这东西叫啥，反正就是下面这个图里进度条上面的那一坨。这个东西实际上是把现在正在播放的音频进行傅里叶变换，画出的频域图。
还有一种应用是视频以及图片的防伪和防盗版鉴别当中。将画面进行二维傅里叶变换，叠加高频分量，再进行逆变换即可。高频分量带来的差异很小，肉眼难以分辨，而且难以通过简单的截图和p图操作消除高频分量，因而是一种十分有效的“水印”。
除此以外，音视频的压缩也可以采用傅里叶变换，只保留强度较高的频率，去除较弱的频率，减少存储的数据量。
